线性代数课程、书籍推荐-Toy模板网

这篇具有很好参考价值的文章主要介绍了线性代数课程、书籍推荐。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1 介绍

1.1 背景

工作中涉及线性代数越来越多，然后开一篇博客补一下知识点。

1.2 教材回顾

大学用的同济版教材，当时学的不好，教材和老师都没说线性代数是干嘛用的，面对枯燥的公式失去了兴趣。
工作中，做3D开发，空间变换用到矩阵运算；做机械臂手眼标定算法用到矩阵运算；卡尔曼滤波算法涉及矩阵运算；多次接触，才重拾取兴趣，觉得线性代数很重要，很有趣。

1.3 推荐学习课程

麻省理工公开课：线性代数 – Gilbert Strang 教授
麻省理工公开课：线性代数
MIT线性代数【全】
Strang 教授 1934 年生于芝加哥，在加州大学洛杉矶分校取得博士学位，从 1962 年起就开始担任麻省理工学院的数学系教授，一辈子都在教书育人、笔耕不辍。去年初，他还出版了一本新书《Linear Algebra and Learning from Data》。
3Blue1Brown 线性代数的本质
3Blue1Brown 线性代数的本质
3Blue1Brown是一个由Grant Sanderson创建的YouTube频道。该频道从独特的视觉角度解说高等数学，内容包括线性代数、微积分、神经网络、黎曼猜想、傅里叶变换以及四元数。
频道创始人Grant Sanderson是斯坦福大学的数学研究生。
斯坦福ENGR108 | 矩阵论与应用线性代数
斯坦福ENGR108 | 矩阵论与应用线性代数
Lecture slides for Introduction to Applied Linear Algebra: Vectors, Matrices, and Least Squares
课程讲师 Stephen Boy，斯坦福教授，是目前全球讲授线性代数、矩阵论方向最著名的老师之一，也是高赞图书《Introduction to Applied Linear Algebra – Vectors, Matrices, and Least Squares（应用线性代数简介——向量、矩阵和最小二乘法）》、《Convex optimization（凸优化）》的联合作者。
Sheldon Axler《Linear Algebra Done Right》
Sheldon Axler《Linear Algebra Done Right》视频
鸢尾花书《矩阵力量》
鸢尾花书《矩阵力量》

2 公式查找

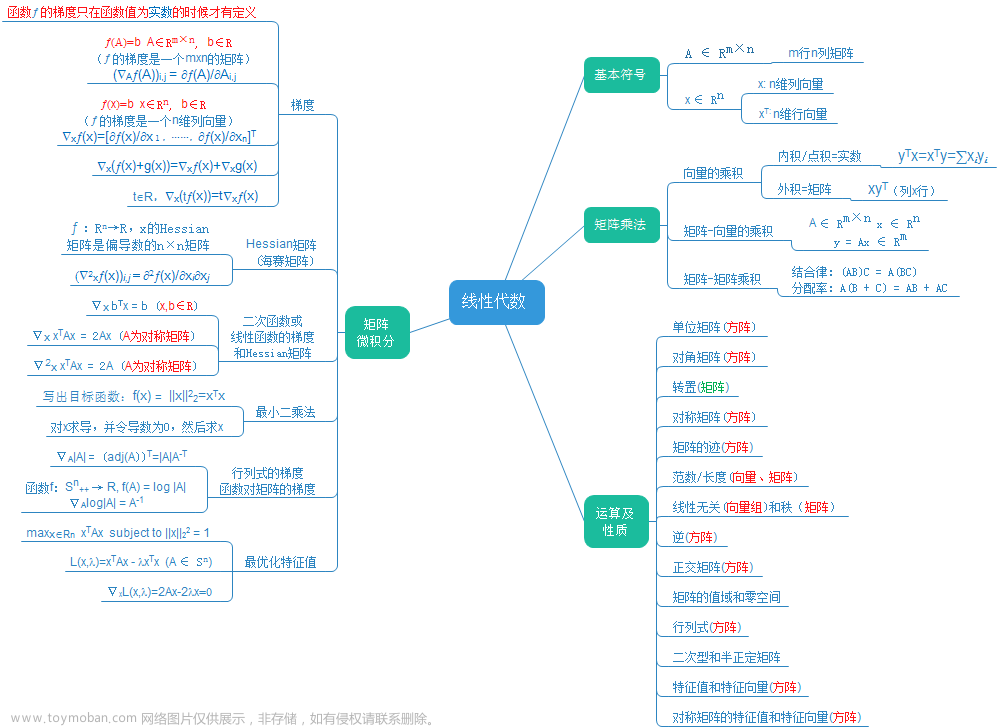
线性代数公式定理一览表

其他

数学入门经典书籍

《数学之美》：这本书由吴军博士写成，内容涵盖了数学中的很多经典问题，包括费马大定理、黎曼猜想等。它用通俗易懂的方式讲解了数学的基本原理和应用。
《线性代数及其应用》：这是由 Gilbert Strang 教授编写的一本经典教材，它对线性代数的基本概念、矩阵论、向量空间等方面进行了详细的讲解。
《微积分学教程》：这是由斯宾诺莎所著的一本经典教材，全书分为微积分基础和微积分应用两部分，内容覆盖了微积分的基本概念、极限、导数、积分等方面。
《概率论与数理统计》：这是由胡宝清教授所编写的一本经典教材，内容包括概率基础、随机变量、概率分布、参数估计、假设检验等方面。
《离散数学及其应用》：这是由罗森教授编写的一本经典教材，内容涵盖了图论、集合论、布尔代数、组合数学等方面。

参考

1、斯坦福ENGR108 | 矩阵论与应用线性代数
2、麻省理工公开课：线性代数
3、3Blue1Brown 线性代数的本质
4、《线性代数》（同济版）——教科书中的…
5、线性代数极简入门
6、线性代数知识汇总
7、Lecture slides for Introduction to Applied Linear Algebra: Vectors, Matrices, and Least Squares
8、学好线性代数，我推荐这本书
9、Sheldon Axler《Linear Algebra Done Right》视频
10、线性代数公式定理一览表
11、理解矩阵（一）
12、鸢尾花书《矩阵力量》文章来源地址https://www.toymoban.com/news/detail-529597.html

到了这里，关于线性代数课程、书籍推荐的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！