目的:以三元组表形式表示稀疏矩阵,实现两个矩阵的加法、减法。
实验步骤
1. 定义三元组存储结构
2. 输入稀疏矩阵:首先应输入矩阵的行数、列数和非零项的数目,并判别给出的两个矩阵的行、列数对于所要求进行的运算是否匹配。可设矩阵的行数和列数均不超过20。接下来逐个输入表示非零元的三元组(i, j, aij),程序可以对三元组的输入顺序加以限制,如按行优先。
3. 进行相关的运算,如加法或减法。
4. 输出结果矩阵(以阵列的形式输出运算结果)。
#include<stdio.h>
#include<stdlib.h>
#define MAXSIZE 20
#define OK 1
#define ERROR 0
//用来存放三元组中每一个非零元素的信息
typedef struct {
int r, c; //行号 列号
int d;//表示非零元的值
} TupNode;
//用来存放三元组矩阵的信息
typedef struct {
int rows, cols, nums; //行数 列数 非零元素个数
TupNode data[MAXSIZE];
} TSMatrix;
//将三元元组表转换成二维数组
void conversionMatrix(TSMatrix *t, int A[t->rows][t->cols]) {
for (int i = 0; i < t->rows; i++) {
for (int j = 0; j < t->cols; j++) {
A[i][j] = 0; //全部元素赋值0
}
}
for (int i = 0; i < t->nums; i++) {
A[t->data[i].r - 1][t->data[i].c - 1] = t->data[i].d;
}
}
//打印矩阵
void printMatrix(TSMatrix *t) {
int A[t->rows][t->cols];
conversionMatrix(t, A);
for (int i = 0; i < t->rows; i++) {
for (int j = 0; j < t->cols; j++) {
printf("%2d ", A[i][j]);//以矩阵形式打印
}
printf("\n");
}
printf("\n");
}
//输入三元组表
int inputMatrix(TSMatrix *t, int n) {
printf("请输入第%d个元组的信息(依次输入行数,列数,非零元个数):\n", n);
scanf("%d%d%d", &t->rows, &t->cols, &t->nums);
//printf("t->rows=%d, t->cols=%d, t->nums=%d\n", t->rows, t->cols, t->nums);
int i, j;
printf("请输入每个三元组矩阵的非零元素的信息:\n");
for (i = 0, j = 0; i < t->nums; i++, j++) {
printf("依次输入第%d个三元组第%d个非零元素行标,列标,数值", n, i + 1);
scanf("%d%d%d", &t->data[i].r, &t->data[i].c, &t->data[i].d);
// printf("t->data[%d].r=%d,t->data[%d].c=%d, t->data[%d]=%d\n", i,t->data[i].r, i,t->data[i].c, i,t->data[i].d);
}
printf("第%d个三元组表矩阵如下:\n", n);
printMatrix(t);
return OK;
}
//三元组表相加
void calculatingMatrix(TSMatrix *t1, TSMatrix *t2, TSMatrix *t) {
if (t1->rows != t2->rows || t1->cols != t2->cols) {
printf("error,该矩阵不能进行加减运算,程序退出\n");
exit(0);
}
int A[t1->rows][t1->cols];
int B[t2->rows][t2->cols];
int C[t1->rows][t1->cols];
int C1[t1->rows][t1->cols]; //存储相减后结果
conversionMatrix(t1, A);
conversionMatrix(t2, B);
printf("相减后三元组表矩阵如下:\n");
for (int i = 0; i < t1->rows; i++) {
for (int j = 0; j < t1->cols; j++) {
C1[i][j] = A[i][j] - B[i][j];
printf("%2d ", C1[i][j]);//以矩阵形式打印
}
printf("\n");
}
printf("相加后三元组表矩阵如下:\n");
for (int i = 0; i < t1->rows; i++) {
for (int j = 0; j < t1->cols; j++) {
C[i][j] = A[i][j] + B[i][j];
printf("%2d ", C[i][j]);//以矩阵形式打印
}
printf("\n");
}
}
int main() {
TSMatrix t1;
TSMatrix t2;
TSMatrix t;
inputMatrix(&t1, 1);
inputMatrix(&t2, 2);
calculatingMatrix(&t1, &t2, &t);
} 文章来源:https://www.toymoban.com/news/detail-531810.html
文章来源:https://www.toymoban.com/news/detail-531810.html
 文章来源地址https://www.toymoban.com/news/detail-531810.html
文章来源地址https://www.toymoban.com/news/detail-531810.html
到了这里,关于【C 数据结构】以三元组表形式表示稀疏矩阵,实现两个矩阵的加法、减法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!



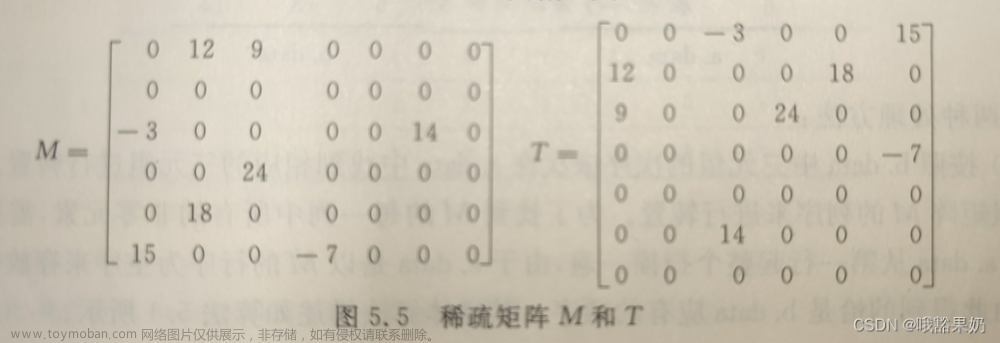
![[数据结构(C语言版本)上机实验]稀疏矩阵的三元组顺序表压缩存储以及转置实现(含快速转置)](https://imgs.yssmx.com/Uploads/2024/02/435123-1.png)







