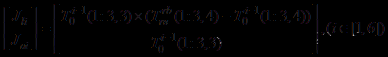【MATLAB】五自由度机械臂运动学逆解（数值法—

这篇具有很好参考价值的文章主要介绍了【MATLAB】五自由度机械臂运动学逆解（数值法——牛顿迭代）实现。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

引言

本篇为五轴机械臂的数值法实现，同时，本方法可应用于六轴、七轴手臂的逆解。
数值法的好处：给定起始与目标位姿，能够自动迭代出最优解，无多解问题
关于解析法的实现，可以看我之前的博客：https://blog.csdn.net/qq_43557907/article/details/122707124
本篇文章是记录我个人在学习时的一些记录，如果各位有发现错误，麻烦在评论区批评或指出，我会第一时间改正，与大家共同学习，谢谢。

一、牛顿迭代

以下是牛顿迭代的基本公式，具体原理可以去B站搜。
五轴反解算法,# Matlab,matlab,矩阵,线性代数

二、构建雅可比矩阵

根据以上思想，
五轴反解算法,# Matlab,matlab,矩阵,线性代数

三、求解思路

五轴反解算法,# Matlab,matlab,矩阵,线性代数

四、MATLAB实现

这里只贴出关键部分，不再赘述

% 牛顿迭代求解逆运动学
syms theta1 theta2 theta3 theta4 theta5; % 定义变量
theta = [theta1 theta2 theta3 theta4 theta5];
T = roboarm_fkine(theta, alpha, d, a);
F = T - T_new;
f1 = F(1,1);f2 = F(1,2);f3 = F(1,3);f4 = F(1,4);
f5 = F(2,1);f6 = F(2,2);f7 = F(2,3);f8 = F(2,4);
f9 = F(3,1);f10 = F(3,2);f11 = F(3,3);f12 = F(3,4);
f = [f1;f2;f3;f4;f5;f6;f7;f8;f9;f10;f11;f12];
i = 1;% 迭代次数
while(i < 1000)
    J_k = subs(jacobian(f, theta), theta, theta_k);
    f_k = subs(f, theta, theta_k);
    theta_k = vpa((theta_k' - pinv(J_k) * f_k)', 4);
    i = i + 1;
    if(norm(f_k) < 0.0001)
        fprintf('Solution has converged');
        break;
    end
end

五、验证

迭代后得出的角度：
五轴反解算法,# Matlab,matlab,矩阵,线性代数
目标角度：

可以看见基本吻合。

参考文献

[1] 张栩曼, 张中哲, 王燕波, 等. 基于空间六自由度机械臂的逆运动学数值解法[J]. 导弹与航天运载技术, 2016 (3): 81-84.
[2] 机器人学导论
[3] 牛顿迭代法求解工业机械人运动学逆解（改进DH模型）https://blog.csdn.net/libizhide/article/details/106078575文章来源地址https://www.toymoban.com/news/detail-532096.html

到了这里，关于【MATLAB】五自由度机械臂运动学逆解（数值法——牛顿迭代）实现的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！