动态规划第1关：数塔问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划第1关：数塔问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

任务描述

本关任务：编写用动态规划解决数塔问题。

编程要求

第1关:数塔问题,动态规划,算法,数据结构

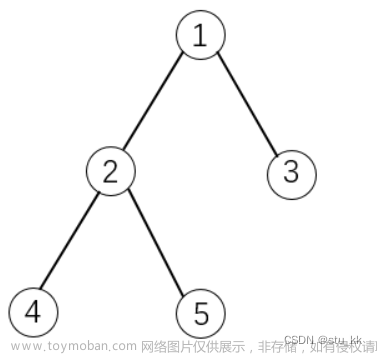
求上图从顶层到顶层的一个路径，使路径上的数字和最大。要求输出最大的数字和max和数值和最大的路径。

解题思路：

原始信息有层数和数塔中的数据，层数用一个整型变量n存储，数塔中的数据用二维数组data，存储成如下的下三角阵:

9
12 15
10 6 8
2 18 9 5
19 7 10 4 16

测试输入：

5
9
12 15
10 6 8
2 18 9 5
19 7 10 4 16

输出示例：文章来源地址https://www.toymoban.com/news/detail-532566.html

max=59
数值和最大的路径是：9->12->10->18->10

#include <stdio.h> 

/********** Begin **********/
#define MAX(a,b)((a) > (b) ? (a) : (b))//宏定义
int main() {
	int a[50][50][4];    
    a[1][1][1]=9;
    a[2][1][1]=12, a[2][2][1]=15;
    a[3][1][1]=10, a[3][2][1]=6,  a[3][3][1]=8;
    a[4][1][1]=2,  a[4][2][1]=18, a[4][3][1]=9,  a[4][4][1]=5;
    a[5][1][1]=19, a[5][2][1]=7,  a[5][3][1]=10, a[5][4][1]=4, a[5][5][1]=16; 
	int dp[50][50];
	int i,j,num[50];
	int g,h,e;
	//把第5行数据放入dp[5][]中 
	for(j=1;j<=5;j++) {
		dp[5][j] = a[5][j][1]; 
	}
	//使用动态规划寻找出最大路径和 
	for(i=4;i>=1;i--) {
		for(j=1;j<=i+1;j++){
			dp[i][j] = MAX(dp[i+1][j],dp[i+1][j+1]) + a[i][j][1];
		}	
	}
	//找出n-2前所有路径值 
	num[4] = dp[4][1];
	for(i=4;i>=1;i--) {
		for(j=1;j<=i;j++) {
			num[i] = MAX(num[i],dp[i][j]);
			//找出n-1行经过路径的值 
			if(dp[i][j] == 28) {
//				printf("i=%d\n",i);
//				printf("j=%d\n",j);
				g = i;
				h = j;
//				printf("%d\n",a[4][2][1]); 
//				printf("%d\n",a[5][3][1]); 
			}
		}
	}
	//找出n行经过路径的值
	for(j=1;j<=5;j++) {
			if(a[g][h][1] + a[5][j][1] == 28) {
				e = j;
			}
	}
	//输出最大路径和 
	printf("max=%d\n",dp[1][1]);
	//遍历输出各行路径值 
	printf("数值和最大的路径是："); 
	for(i=1;i<=5;i++) {
		if(i <= 3) {
			printf("%d->",num[i]-num[i+1]);
		} else if(i==4) {
			num[4] = a[g][h][1];
			printf("%d->",num[i]);
		} else if(i==5) {
			num[5] = a[5][e][1];
			printf("%d\n",num[i]);
			}
	}
    return 0;
}
/********** End **********/

到了这里，关于动态规划第1关：数塔问题的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！