第六课 解方程组
1/6判断方程组解的情况
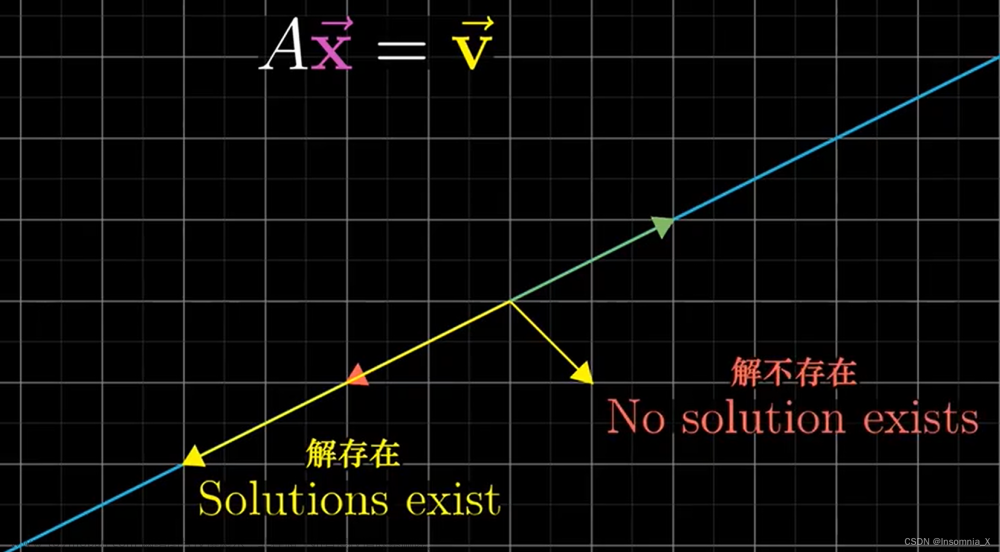
判断方程组的解的情况：
齐次唯一解例题：
非齐次无解例题：
非齐次有解例题：
2/6解方程组
解方程组：共有五步
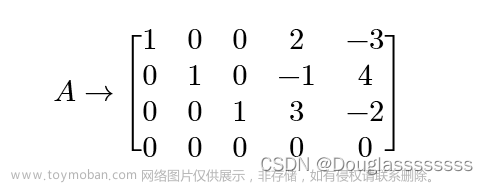
①求增广矩阵的秩：
②变换矩阵：
R=3，就变换前三行，前三列，为单位矩阵的形式
③ 根据②得到的矩阵变回方程组：
④设未知数：
⑤整理成标准型，再用刚刚设的未知数替代题目原来的未知数：
这里④中我们只设置了一个未知数K，则在⑤中为用k替代X4
下面就是本题的解，k可取任意值：
例题(非齐次)
这里④中我们设置了三个未知数K1、K2、K3，则在⑤中为用K1替代X5、K2替代X4、K3替代X3
例题(齐次)
如果是齐次方程组呢？
常数项都抹掉就完了、
3/6 求方程组的通解、特解、基础解系
求方程组的通解、特解。基础解系：
要先解出方程组的解。
通解，含有所有的未知数，能代表所有情况的解
①求方程组的通解
②求方程组的特解
特解就是**一组x1–xn的值**，代入原方程，可以满足：
也就是未知数随便取值：这是一个特解
一般都令所有未知数=0,这样可以简化计算量
③求方程组的基础解系
4/6 已知某方程组多个特解，求某齐次方程组的通解
解题步骤共三步：
①设未知数：
结果为：
设有未知数
k
1
、
k
2
设有未知数k_1、k_2
设有未知数k1、k2
②找出n个线性无关的矩阵X1，X2，…Xn，使其替代x，满足要求通解的式子
③求通解
5/6 已知某方程组多个特解，求某非齐次方程组的通解
非齐次方程组的通解=对应齐次方程组的通解（①②③）+非齐次方程组的特解（④）
解题步骤共四步：
①设未知数：
结果为：
设有未知数
k
1
、
k
2
设有未知数k_1、k_2
设有未知数k1、k2
②找出n个线性无关的矩阵X1，X2，…Xn，使其替代x，满足去掉参数项后的要求通解的式子
③找出一个矩阵Y，使其满足要求通解的式子
④求通解
6/6 判断解集合中线性无关的解向量的个数
直接背公式：
①齐次
文章来源：https://www.toymoban.com/news/detail-532602.html
②非齐次
文章来源地址https://www.toymoban.com/news/detail-532602.html
到了这里，关于线代【解方程组】--猴博士爱讲课的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
