迪杰斯特拉(Dijkstra)算法是由荷兰计算机科学家狄克斯特拉于1959年提出的。是寻找从一个顶点到其余各顶点的最短路径算法,可用来解决最短路径问题。
迪杰斯特拉算法采用贪心算法的策略,将所有顶点分为已标记点和未标记点两个集合,从起始点开始,不断在未标记点中寻找距离起始点路径最短的顶点,并将其标记,直到所有顶点都被标记为止。需要注意的一点是该方法不能处理带有负权边的图,下面我们举出一个实例并通过迪杰斯特拉方法对其进行求解。
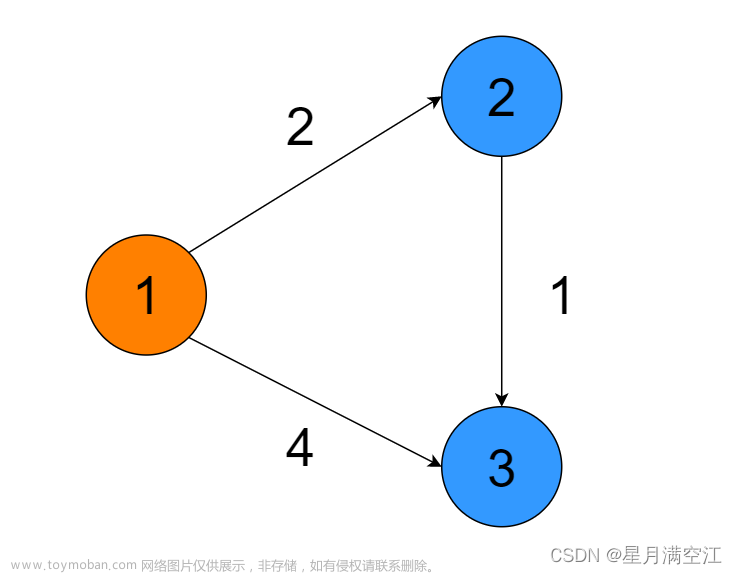
图1所示为一个最短路径问题,每条边代表一条路径,边上的数值表示这条边的长度。

我们用迪杰斯特拉方法寻找从顶点0到顶点5的最短路径。标号结果如图2所示,图中括号里的两个数分别表示该点的父顶点标号和初始点到该点的最短路径长度。由图2可知,从节点0到节点5的最短路径长度为9,最短路径为:0 -> 2 -> 3 -> 5。

下面我们考虑通过java语言来实现用迪杰斯特拉算法寻找图一中的顶点0到顶点5的最短路径问题。
我们首先创建一个顶点类,属性包括id、父点和到起始点的最短距离。主方法主要分为五个部分,在第一部分进行数据的初始化;第二个部分新建一个已标记点集合,创建一个点对象作为起始顶点加入到已标记点集合中;第二部分新建一个未标记点集合,创建其余5个点并添加到未标记点集合中;第三部分为一个while循环,功能是不断的将未标记点集合中的点转移到已标记点集合中去;第五部分是路径的输出。在第四部分,每个循环中我们需要寻找要进行标记的顶点,因此我们创建了一个寻找要标记顶点的函数,其功能是在所有未标记点中寻找距离起始顶点距离最短的顶点,具体过程如下:
初始时,已标记点集合中只有源节点,未标记点集合中包含剩余所有节点。随后进入迭代,每次迭代时,首先探索从已标记节点(如vi)流出的所有有向弧,找到流出弧的尾部节点(如vj),计算从vi到vj的费用和收益以及到源节点的利润(vj到源节点的利润=vi到源节点的利润+vi到vj的利润),若该利润大于vj到源节点的最大利润,将vj到源节点的最大利润更新为该利润,将vi标记为vj的上一个节点。未标记点集合遍历完成后,若节点vj满足在所有未标记点中到源节点的利润最大,将节点vj添加到已标记点集合,并在未标记点集合中删除节点vj。
不断重复上述操作,直至未标记点集合为空集。迪杰斯特拉算法就是将所有顶点分为已标记点和未标记点两个集合,从起始点开始,不断在未标记点中寻找距离起始点利润最大的节点,并将其标记,直到所有顶点都被标记为止。详细代码如下:文章来源:https://www.toymoban.com/news/detail-533071.html
import java.util.ArrayList;
import java.util.List;
public class Dijkstra {
static int[][] matrix = new int[6][6];
final static int N = 10000;
public static void main(String[] args) {
//邻接矩阵
matrix[0] = new int[]{0, 6, 3, N, N, N};/*1*/
matrix[1] = new int[]{6, 0, 2, 5, N, N};/*2*/
matrix[2] = new int[]{3, 2, 0, 3, 4, N};/*3*/
matrix[3] = new int[]{N, 5, 3, 0, 2, 3};/*4*/
matrix[4] = new int[]{N, N, 4, 2, 0, 5};/*5*/
matrix[5] = new int[]{N, N, N, 3, 5, 0};/*6*/
//已标记点集合
List<Vertex> Marked = new ArrayList<>();
Vertex vt0 = new Vertex();
vt0.id = 0;
vt0.minLenth = 0;
Marked.add(vt0);
//未标记点集合
List<Vertex> UnMarked = new ArrayList<>();
for (int i = 0; i < 5; i++) {
Vertex vtx = new Vertex();
vtx.id = i+1;
UnMarked.add(vtx);
}
//将未标记点集合中的点转移到已标记点集合
int order = 1;
while(!UnMarked.isEmpty()){
Vertex vtx = FindVer(Marked, UnMarked);
UnMarked.remove(vtx);
Marked.add(vtx);
System.out.println("第"+order+"次标号,顶点"+vtx.id+"的标号为:(" + vtx.father.id + "," +vtx.minLenth + ")");
order++;
}
//输出路径
for(Vertex v :Marked){
if(v.id == 5){
System.out.println("0-5的最短路径长度为:" + v.minLenth);
System.out.print("逆推得最优路径为:" + "5");
while(v.id != 0){
v = v.father;
System.out.print( " -> " + v.id);
}
}
}
}
static Vertex FindVer(List<Vertex> Marked, List<Vertex> UnMarked){
int M = 10000;
Vertex v = null;
for (Vertex ve : UnMarked) {
for (Vertex vr : Marked) {
int all_p = vr.minLenth + matrix[vr.id][ve.id];
if (all_p <= ve.minLenth) {
ve.minLenth = all_p;
ve.father = vr;
}
}
if (ve.minLenth < M) {
M = ve.minLenth;
v = ve;
}
}
return v;
}
}
class Vertex {
public int id;
public Vertex father;
public int minLenth = 10000;
}
程序的运行结果如下:文章来源地址https://www.toymoban.com/news/detail-533071.html
第1次标号,顶点2的标号为:(0,3)
第2次标号,顶点1的标号为:(2,5)
第3次标号,顶点3的标号为:(2,6)
第4次标号,顶点4的标号为:(2,7)
第5次标号,顶点5的标号为:(3,9)
0-5的最短路径长度为:9
逆推得最优路径为:5 -> 3 -> 2 -> 0
进程已结束,退出代码0到了这里,关于java实现迪杰斯特拉(Dijkstra)算法求解最短路问题的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!