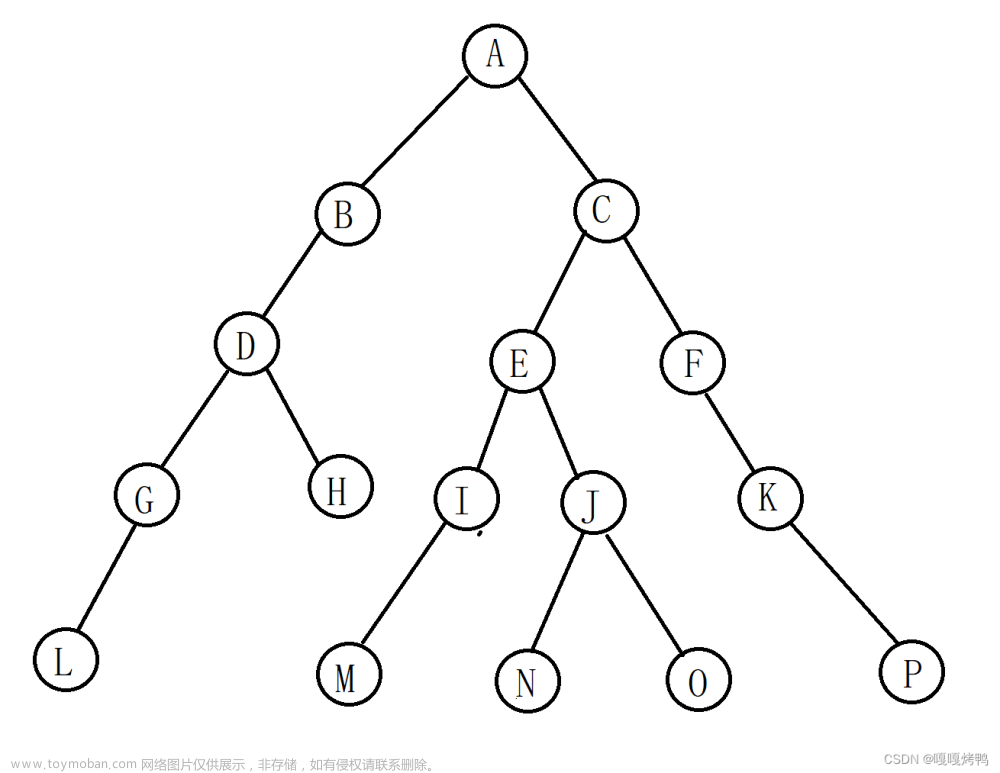
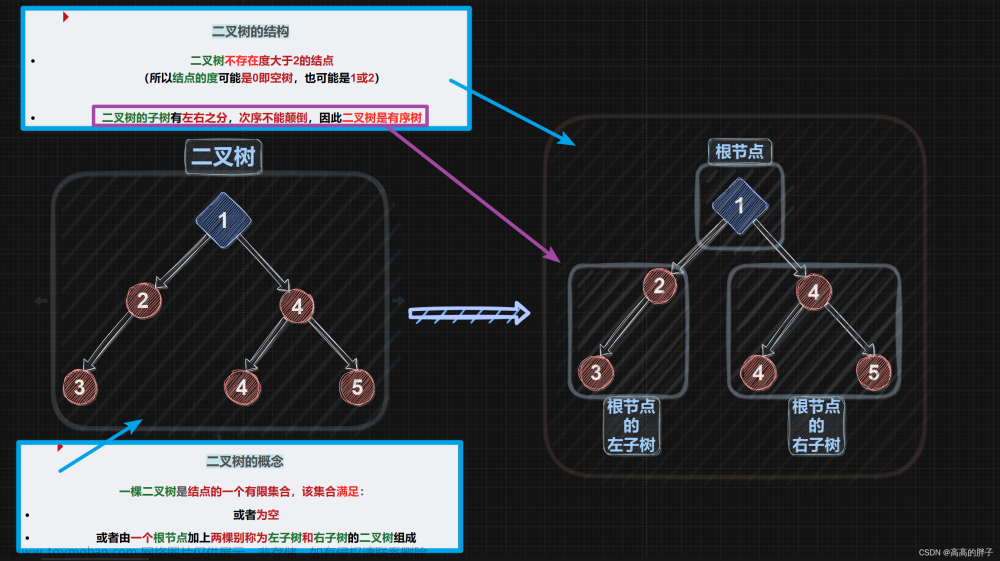
Trie字典树主要用于存储字符串,Trie 的每个 Node 保存一个字符。用链表来描述的话,就是一个字符串就是一个链表。每个Node都保存了它的所有子节点。
例如我们往字典树中插入see、pain、paint三个单词,Trie字典树如下所示:

也就是说如果只考虑小写的26个字母,那么Trie字典树的每个节点都可能有26个子节点。
Trie字典树的基本操作
插入
本文是使用链表来实现Trie字典树,字符串的每个字符作为一个Node节点,Node主要有两部分组成:
- 是否是单词 (boolean isWord)
- 节点所有的子节点,用map来保存 (Map next)
例如插入一个paint单词,如果用户查询pain,尽管 paint 包含了 pain,但是Trie中仍然不包含 pain 这个单词,所以如果往Trie中插入一个单词,需要把该单词的最后一个字符的节点的 isWord 设置为 true。所以为什么Node需要存储 是否是单词 这个属性。
节点的所有子节点,通过一个Map来存储,key是当前子节点对应的字符,value是子节点。
实现的伪代码如下:
public void add(String word) {
Node current = root;
char[] cs = word.toCharArray();
for (char c : cs) {
Node next = current.next.get(c);
if (next == null) {
//一个字符对应一个Node节点
current.next.put(c, new Node());
}
current = current.next.get(c);
}
//current就是word的最后一个字符的Node
//如果当前的node已经是一个word,则不需要添加
if (!current.isWord) {
size++;
current.isWord = true;
}
}复制
查找
Trie查找操作就比较简单了,遍历带查找的字符串的字符,如果每个节点都存在,并且待查找字符串的最后一个字符对应的Node的 isWord 属性为 true ,则表示该单词存在,伪代码如下:
public boolean contains(String word) {
Node current = root;
for (int i = 0; i < word.length(); i++) {
char c = word.charAt(i);
Node node = current.next.get(c);
if (node == null) {
return false;
}
current = node;
}
//current就是word的最后一个字符的Node
return current.isWord;
}复制
前缀查询
前缀查询和上面的查询操作基本类似,就是不需要判断 isWord 了
public boolean containsPrefix(String prefix) {
Node current = root;
for (int i = 0; i < prefix.length(); i++) {
char c = prefix.charAt(i);
Node node = current.next.get(c);
if (node == null) {
return false;
}
current = node;
}
return true;
}复制
删除
Trie的删除操作就稍微复杂一些,主要分为以下3种情况:
如果单词是另一个单词的前缀
如果待删除的单词是另一个单词的前缀,只需要把该单词的最后一个节点的 isWord 的改成false
比如Trie中存在 panda 和 pan 这两个单词,删除 pan ,只需要把字符 n 对应的节点的 isWord 改成 false 即可
如下图所示

如果单词的所有字母的都没有多个分支,删除整个单词
如果单词的所有字母的都没有多个分支(也就是说该单词所有的字符对应的Node都只有一个子节点),则删除整个单词
例如要删除如下图的see单词,如下图所示:

如果单词的除了最后一个字母,其他的字母有多个分支

基于链表的Trie字典树
public class Trie {
private Node root;
private int size;
private static class Node {
public boolean isWord;
public Map<Character, Node> next;
public Node() {
next = new TreeMap<>();
}
public Node(boolean isWord) {
this();
this.isWord = isWord;
}
}
public Trie() {
root = new Node();
}
public int size() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
/**
* 插入操作
*
* @param word 单词
*/
public void add(String word) {
Node current = root;
char[] cs = word.toCharArray();
for (char c : cs) {
Node next = current.next.get(c);
if (next == null) {
current.next.put(c, new Node());
}
current = current.next.get(c);
}
//如果当前的node已经是一个word,则不需要添加
if (!current.isWord) {
size++;
current.isWord = true;
}
}
/**
* 是否包含某个单词
*
* @param word 单词
* @return 存在返回true,反之false
*/
public boolean contains(String word) {
Node current = root;
for (int i = 0; i < word.length(); i++) {
char c = word.charAt(i);
Node node = current.next.get(c);
if (node == null) {
return false;
}
current = node;
}
//如果只存在 panda这个词,查询 pan,虽然有这3个字母,但是并不存在该单词
return current.isWord;
}
/**
* Trie是否包含某个前缀
*
* @param prefix 前缀
* @return
*/
public boolean containsPrefix(String prefix) {
Node current = root;
for (int i = 0; i < prefix.length(); i++) {
char c = prefix.charAt(i);
Node node = current.next.get(c);
if (node == null) {
return false;
}
current = node;
}
return true;
}
/*
* 1,如果单词是另一个单词的前缀,只需要把该word的最后一个节点的isWord的改成false
* 2,如果单词的所有字母的都没有多个分支,删除整个单词
* 3,如果单词的除了最后一个字母,其他的字母有多个分支,
*/
/**
* 删除操作
*
* @param word
* @return
*/
public boolean remove(String word) {
Node multiChildNode = null;
int multiChildNodeIndex = -1;
Node current = root;
for (int i = 0; i < word.length(); i++) {
Node child = current.next.get(word.charAt(i));
//如果Trie中没有这个单词
if (child == null) {
return false;
}
//当前节点的子节点大于1个
if (child.next.size() > 1) {
multiChildNodeIndex = i;
multiChildNode = child;
}
current = child;
}
//如果单词后面还有子节点
if (current.next.size() > 0) {
if (current.isWord) {
current.isWord = false;
size--;
return true;
}
//不存在该单词,该单词只是前缀
return false;
}
//如果单词的所有字母的都没有多个分支,删除整个单词
if (multiChildNodeIndex == -1) {
root.next.remove(word.charAt(0));
size--;
return true;
}
//如果单词的除了最后一个字母,其他的字母有分支
if (multiChildNodeIndex != word.length() - 1) {
multiChildNode.next.remove(word.charAt(multiChildNodeIndex + 1));
size--;
return true;
}
return false;
}
}复制
基于Trie的Set性能对比
现在使用Trie实现下Set集合,然后三者性能做一个比较,还是以傲慢与偏见、双城记、战争与和平三本原著作为数据源。
傲慢与偏见(Pride and Prejudice)的性能对比
Pride and Prejudice
Total words: 125901
Total different words: 6530
TrieSet Time: 0.099788784
BSTSet Time: 0.339963625
LinkedListSet Time: 3.554973381复制
从中可以看出傲慢与偏见不同的单词只有6000左右,阅读难度不是很大。
双城记(A Tale of Two Cities)的性能对比
A Tale of Two Cities
Total words: 141489
Total different words: 9944
TrieSet Time: 0.119505174
BSTSet Time: 0.331334495
LinkedListSet Time: 5.26063235复制
战争与和平(War and peace)的性能对比
War and Peace
Total words: 602359
Total different words: 16725
TrieSet Time: 0.09750872
BSTSet Time: 0.233328074复制
以上关于原著词汇的统计只是简单的对比单词是否一致,并没有考虑一个单词的过去式、进行时等时态,只要字符串不一致都把它当作不同的单词。
更多关于Trie的话题
上面实现的Trie中,我们是使用TreeMap来保存节点的所有的子节点,也可以使用HashMap来保存所有的子节点,效率更高:
public Node() {
next = new HashMap<>();
}复制
当然我们也可以使用一个定长的数组来存储所有的子节点,效率比HashMap更高,因为不需要使用hash函数:
public Node(boolean isWord){
this.isWord = isWord;
next = new Node[26];//只能存储26个小写字母
}复制
Trie查询效率非常高,但是对空间的消耗还是挺大的,这也是典型的空间换时间。
可以使用 压缩字典树(Compressed Trie) ,但是维护相对来说复杂一些。
如果我们不止存储英文单词,还有其他特殊字符,那么维护子节点的集合可能会更多。
可以对Trie字典树做些限制,比如每个节点只能有3个子节点,左边的节点是小于父节点的,中间的节点是等于父节点的,右边的子节点是大于父节点的,这就是三分搜索Trie字典树(Ternary Search Trie)。
LeetCode相关线段树的问题
LeetCode第208号问题
问题描述:
实现一个 Trie (前缀树),包含 insert, search, 和 startsWith 这三个操作。
示例:
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 true
trie.search("app"); // 返回 false
trie.startsWith("app"); // 返回 true
trie.insert("app");
trie.search("app"); // 返回 true复制
问题说明:
你可以假设所有的输入都是由小写字母 a-z 构成的。 保证所有输入均为非空字符串。
这个问题在我们实现的 Trie字典树 中已经实现了这个功能了,add()就是对应的insert(),contains()就是对应的search(),starcontainsPrefix()就是对应的startsWith(),这里就不贴代码了。
LeetCode第211号问题
问题描述:
设计一个支持以下两种操作的数据结构:
void addWord(word)
bool search(word)
search(word) 复制
可以搜索文字或正则表达式字符串,字符串只包含字母 . 或 a-z 。 . 可以表示任何一个字母。
示例:
addWord("bad")
addWord("dad")
addWord("mad")
search("pad") -> false
search("bad") -> true
search(".ad") -> true
search("b..") -> true复制
问题说明:
你可以假设所有单词都是由小写字母 a-z 组成的。
这个问题就是上一个问题的基础上加上 . 的处理,稍微复杂点。
如果下一个字符是 . ,那么需要遍历该节点的所有子节点,对所有子节点的处理就是一个递归程序:
public boolean searchByWildCard(String express) {
return search(root, express, 0);
}
private boolean search(Node node, String express, int index) {
//如果已经到了待查询字符串的尾端了
if (index == express.length()) {
return node.isWord;
}
char c = express.charAt(index);
if (c != '.') {
Node nextChar = node.next.get(c);
if (nextChar == null) {
return false;
}
return search(nextChar, express, index + 1);
} else {//如果是通配符
Map<Character, Node> nextNodes = node.next;
//遍历所有的子节点
for (Map.Entry<Character, Node> entry : nextNodes.entrySet()) {
if (search(entry.getValue(), express, index + 1)) {
return true;
}
}
return false;
}
}复制
LeetCode第677号问题
问题描述:
实现一个 MapSum 类里的两个方法,insert 和 sum。
对于方法 insert,你将得到一对(字符串,整数)的键值对。字符串表示键,整数表示值。如果键已经存在,那么原来的键值对将被替代成新的键值对。
对于方法 sum,你将得到一个表示前缀的字符串,你需要返回所有以该前缀开头的键的值的总和。
示例 1:
输入: insert("apple", 3), 输出: Null
输入: sum("ap"), 输出: 3
输入: insert("app", 2), 输出: Null
输入: sum("ap"), 输出: 5复制
总结一句话就是,求出所有符合该前缀的字符串的键值的总和。文章来源:https://www.toymoban.com/news/detail-533324.html
节点需要保存一个键值,用于求和。节点Node不需要维护 isWord 这个属性了,因为不关注是不是一个单词。文章来源地址https://www.toymoban.com/news/detail-533324.html
class Node {
public int value;
public Map<Character, Node> next;
}
public int sum(String prefix) {
Node cur = root;
for (int i = 0; i < prefix.length(); i++) {
char c = prefix.charAt(i);
Node node = cur.next.get(c);
if (node == null) {
return 0;
}
cur = node;
}
//cur指向prefix的最后一个字符的Node
//对每个以prefix为前缀的node进行累加
return countValue(cur);
}
private int countValue(Node node) {
int result = node.value;
for (char c : node.next.keySet()) {
result += countValue(node.next.get(c));
}
return result;
}到了这里,关于字典树的数据结构的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!