纸牌博弈问题--动态规划(java)-Toy模板网

这篇具有很好参考价值的文章主要介绍了纸牌博弈问题--动态规划(java)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

纸牌博弈题目描述

给定一个整型数组arr，
代表数值不同的纸牌排成一条线
玩家A和玩家B依次拿走每张纸牌规定玩家A先拿，
玩家B后拿
但是每个玩家每次只能拿走最左或最右的纸牌
玩家A和玩家B都绝顶聪明 (都在拿最优解)
请返回最后获胜者的分数

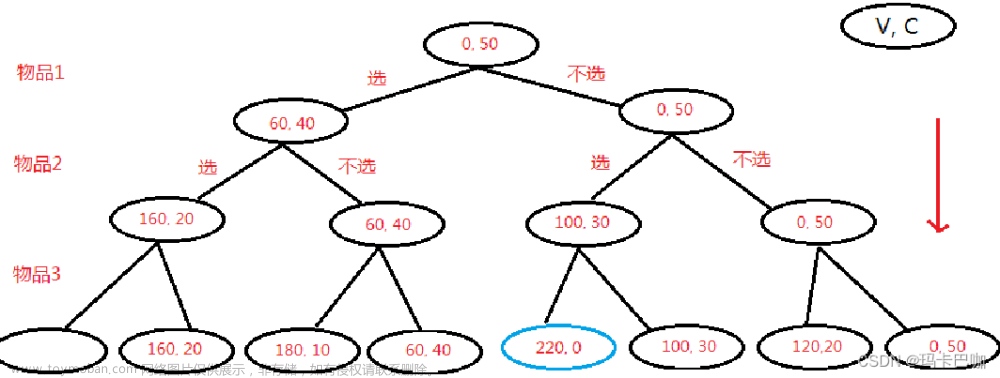
暴力递归

解题思路.
递归就是可虑所有可能性,然后比较出最值,
因此递归就是,不断比较我拿左边和拿右边时,哪个是最优解.
此时.难点在于,还有个后手拿牌的B.
他也是要拿当前的最优解,
这就形成了一个嵌套.
A 拿完一张后,他后面拿牌要在B 拿完后再拿,
两个嵌套的递归思路就形成了,

代码演示

  /**
     * 暴力递归求最值
     * @param arr
     * @return
     */
    public static int win(int[]arr){
        if (arr == null || arr.length == 0){
            return 0;
        }
        //先手
        int f = f(arr, 0, arr.length - 1);
        //后手
        int g = g(arr,0, arr.length - 1) ;
        return Math.max(f,g);
    }

    /**
     * 先手可以拿到的最大值
     * @param arr
     * @param L
     * @param R
     * @return
     */
    public static int f(int[]arr,int L,int R){
    //base case 剩一张 就归先手方
        if(L == R){
            return arr[L];
        }
        //选择一张牌后,剩下要在后手选择后的里继续做选择,
        //后手方也有两种选择情况,都列出来,
        int p1 = arr[L] + g(arr,L + 1,R);
        int p2 = arr[R] + g(arr,L,R - 1);
        //我们取最优解
        return Math.max(p1,p2);
    }

    /**
     * 后手可以拿到的最大值
     * @param arr
     * @param L
     * @param R
     * @return
     */
    public static int g(int[]arr,int L,int R){
    	//剩一张时,后手方啥都拿不到,因为先手会拿走.
        if (L == R){
            return 0;
        }
        //先手拿牌后,后手方只能在先手选择剩下的里去先择
        //因此把先手拿牌的两种情况都算出来
        int g1 = f(arr,L + 1,R);
        int g2 = f(arr,L,R - 1);
        //取最小值是因为,先手一定会把当前最优解拿走,
        //留给后手方一个差一点的值,所以取最小
        return Math.min(g1,g2);
    }

递归 + 缓存

找出暴力递归重复计算的地方,
放进缓存,
这里面重复计算的是什么呢.
就是L R 位置选择会有不断的重复.
用缓存做成记忆化搜索,

代码演示

   /**
     * 递归加缓存求最值
     * @param arr
     * @return
     */
    public static int maxCards(int[]arr){
        if (arr == null || arr.length == 0){
            return 0;
        }
        int N = arr.length;;
        //缓存先手拿牌的最值问题
        int[][]fs = new int[N][N];
        //缓存后手拿牌的最值问题
        int[][]gs = new int[N][N];
        for (int i  = 0;i < N ;i++){
            for (int j = 0; j < N;j++){
                fs[i][j] = -1;
                gs[i][j] = -1;
            }
        }
        int f1 = f1(arr, 0, N - 1, fs, gs);
        int g1 = g1(arr, 0, N - 1, fs, gs);
        return Math.max(f1,g1);
    }

    /**
     * 和递归是一样的,只是把结果放进缓存里.
     * @param arr
     * @param L
     * @param R
     * @param fs
     * @param gs
     * @return
     */
    public static int f1(int[]arr,int L,int R,int[][]fs,int[][]gs){
        if (fs[L][R] != -1){
            return fs[L][R];
        }
        int ans = 0;
        if(L == R){
            ans = arr[L];
        }else {
            int p1 = arr[L] + g1(arr,L + 1,R,fs,gs);
            int p2 = arr[R] + g1(arr,L ,R - 1,fs,gs);
            ans = Math.max(p1,p2);
        }
        fs[L][R] = ans;
        return ans;
    }

    /**
     *
     * @param arr
     * @param L
     * @param R
     * @param fs
     * @param gs
     * @return
     */
    public static int g1(int[]arr,int L,int R,int[][]fs,int[][]gs){
        if (gs[L][R] != -1){
            return gs[L][R];
        }
        int ans = 0;
        if (L != R){
            int p1 = f1(arr,L + 1,R,fs,gs);
            int p2 = f1(arr,L,R - 1,fs,gs);
            ans = Math.min(p1,p2);
        }
        gs[L][R] = ans;
        return ans;
    }

动态规划

动态规划和递归加缓存方式的区别就是,动态规划直接把缓存表先求出来,然后取值,在缓存表中拿,

代码演示

  /**
     * 动态规划
     * @param arr
     * @return
     */
    public static int dp(int[]arr){
        if (arr == null || arr.length == 0){
            return 0;
        }
        int N = arr.length;
        int[][]fs = new int[N][N];
        int[][]gs = new int[N][N];
        for (int i = 0; i < N ;i++){
            fs[i][i] = arr[i];
        }
        for (int i = 1; i < N ;i++){
            int L = 0;
            int R = i;
            while (R < N ){
            	//就是把递归方法换成从缓存表里拿,策略是一样的
                int p1 = arr[L] + gs[L + 1][R];
                int p2 = arr[R] + gs[L][R - 1];
                fs[L][R] = Math.max(p1,p2);
                int g1 =fs[L + 1][R];
                int g2= fs[L][R - 1];
                gs[L][R] = Math.min(g1,g2);
                L++;
                R++;

            }
        }
        return Math.max(fs[0][N - 1],gs[0][N - 1]);
    }