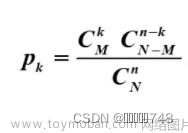第四章基于概率论的分类方法：朴素贝叶斯-Toy模板网

这篇具有很好参考价值的文章主要介绍了第四章基于概率论的分类方法：朴素贝叶斯。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

第四章基于概率论的分类方法：朴素贝叶斯

4.1基于贝叶斯理论的分类方法

朴素贝叶斯

优点：在数据较少的情况下仍然有效，可以处理多类别问题。
缺点：对于输⼊数据的准备⽅式较为敏感。
适⽤数据类型：标称型数据。

假设类别为 $c_1,c_2$ ：

如果 $p 1 (x, y) > p 2 (x, y)$ ，那么类别为 $c_1$
如果 $p 2 (x, y) > p 1 (x, y)$ ，那么类别为 $c_2$

4.2条件概率

$p(c|x)=\frac{p(x|c)p(c)}{p(x)}$

4.3使用条件概率来分类

假设类别为 $c_1,c_2$ ：

如果 $p1(c_1|x,y) > p2(c_2|x,y)$ ，那么类别为 $c_1$
如果 $p2(c_1|x,y) > p1(c_2|x,y)$ ，那么类别为 $c_2$

4.5使用python进行文本分类

4.5.1准备数据

def loadDataSet():
    postingList = [['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                   ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                   ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                   ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                   ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                   ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0, 1, 0, 1, 0, 1]    #1 is abusive, 0 not
    return postingList, classVec

def createVocabList(dataSet):
    vocabSet = set([])  #create empty set
    for document in dataSet:
        vocabSet = vocabSet | set(document) #union of the two sets
    return list(vocabSet)
postingList, classVec=loadDataSet()
print(postingList)
print(classVec)
vocabList=createVocabList(postingList)
print(vocabList)

[['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'], ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'], ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'], ['stop', 'posting', 'stupid', 'worthless', 'garbage'], ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'], ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
[0, 1, 0, 1, 0, 1]
['to', 'licks', 'food', 'I', 'park', 'quit', 'how', 'maybe', 'is', 'has', 'him', 'garbage', 'buying', 'help', 'not', 'flea', 'so', 'problems', 'stupid', 'worthless', 'dog', 'ate', 'please', 'love', 'my', 'posting', 'stop', 'steak', 'cute', 'mr', 'dalmation', 'take']

loadDataSet产生数据集，表示若干句子，句子中若干单词
createVocabList对数据集进行操作，最后返回postingList和classVec
postingList为单词表，即数据集中出现的所有单词vocabList=[‘has’, ‘please’, ‘I’,…,‘dalmation’, ‘licks’]
classVec,表示每个句子是否含有侮辱性，是则为1，classVec=[0, 1, 0, 1, 0, 1]

4.5.2训练算法

def setOfWords2Vec(vocabList, inputSet):
    returnVec = [0]*len(vocabList)
    for word in inputSet:
        returnVec[vocabList.index(word)] = 1
    return returnVec
print(setOfWords2Vec(vocabList,postingList[0]))

[0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0]

setOfWords2Vec函数，返回长度为单词表长度的向量
输入是，单词表vocabList和句子inputSet
inputSet中出现的单词，单词表对应位置的向量位置标记为1

def getTrainMatrix(vocabList,inputSets):
    return [setOfWords2Vec(vocabList, inputSet) for inputSet in inputSets]
trainMatrix=getTrainMatrix(vocabList,postingList)
print(trainMatrix)

[[0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0],
 [1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1],
 [0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0],
 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0],
 [1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0],
 [0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]

getTrainMatrix将若干句子全部转成向量、向量组成列表，这就成了一个矩阵trainMatrix。

import numpy as np
def trainNB0(trainMatrix, trainCategory):
    numTrainDocs = len(trainMatrix)
    numWords = len(trainMatrix[0])
    pAbusive = sum(trainCategory)/numTrainDocs
#     print('trainCategory: ',trainCategory)
#     print('numTrainDocs: ',numTrainDocs)
    p0Num = np.ones(numWords); p1Num = np.ones(numWords)      #change to np.ones()
    p0Denom = 0; p1Denom = 0                       #change to 2.0
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:
            p1Num += trainMatrix[i]
            p1Denom += sum(trainMatrix[i])
        else:
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])
#     p1Vect = np.log(p1Num/p1Denom)          #change to np.log()
#     p0Vect = np.log(p0Num/p0Denom)         #change to np.log()
    p1Vect = p1Num/p1Denom          
    p0Vect = p0Num/p0Denom         
    print(p1Num)  
    print(p1Denom)
    return p0Vect, p1Vect, pAbusive
print(classVec)
p0Vect, p1Vect, pAbusive=trainNB0(trainMatrix,classVec)
print(p0Vect)
print(p1Vect)
print(pAbusive)

[0, 1, 0, 1, 0, 1]
[2. 1. 2. 1. 2. 2. 1. 2. 1. 1. 2. 2. 2. 1. 2. 1. 1. 1. 4. 3. 3. 1. 1. 1.
 1. 2. 2. 1. 1. 1. 1. 2.]
19
[0.08333333 0.08333333 0.04166667 0.08333333 0.04166667 0.04166667
 0.08333333 0.04166667 0.08333333 0.08333333 0.125      0.04166667
 0.04166667 0.08333333 0.04166667 0.08333333 0.08333333 0.08333333
 0.04166667 0.04166667 0.08333333 0.08333333 0.08333333 0.08333333
 0.16666667 0.04166667 0.08333333 0.08333333 0.08333333 0.08333333
 0.08333333 0.04166667]
[0.10526316 0.05263158 0.10526316 0.05263158 0.10526316 0.10526316
 0.05263158 0.10526316 0.05263158 0.05263158 0.10526316 0.10526316
 0.10526316 0.05263158 0.10526316 0.05263158 0.05263158 0.05263158
 0.21052632 0.15789474 0.15789474 0.05263158 0.05263158 0.05263158
 0.05263158 0.10526316 0.10526316 0.05263158 0.05263158 0.05263158
 0.05263158 0.10526316]
0.5

开始算条件概率，如计算侮辱性的条件概率p1Vect，那么就该词侮辱性次数/侮辱总次数：p1Num/p1Denom

p1Num=[2. 1. 2. 1. … 4. 3. 3. 1. 1. 2.],p1Denom=19
p1Vect=[0.10526316 … 0.05263158 0.10526316]

4.5.3测试算法

def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
    p1 = sum(vec2Classify * p1Vec) 
    p0 = sum(vec2Classify * p0Vec) 
#     print('p1:',p1,',  p0:',p0)
    if p1 > p0:
        return 1
    else:
        return 0

def testingNB():
    p0V, p1V, pAb = trainNB0(trainMatrix, classVec)
    testEntrys = [['love', 'my', 'dalmation'],['stupid', 'garbage']]
    for testEntry in testEntrys:
        thisDoc = setOfWords2Vec(myVocabList, testEntry)
        print(testEntry, 'classified as: ', classifyNB(thisDoc, p0V, p1V, pAb))
#     print('thisDoc:',thisDoc)
#     print('p0V:',p0V)
#     print('p1V:',p1V)
testingNB()

['love', 'my', 'dalmation'] classified as:  0
['stupid', 'garbage'] classified as:  1

可以看出，经过小数据集训练，朴素贝叶斯模型可对简单的句子可以进行正确分类文章来源地址https://www.toymoban.com/news/detail-534878.html

到了这里，关于第四章基于概率论的分类方法：朴素贝叶斯的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

第四章基于概率论的分类方法：朴素贝叶斯