1.背景介绍
在介绍所提出的算法的步骤之前,需要知道(i)布朗运动和(ii)莱维运动的两个主要随机游动的数学模型。
1.1 布朗运动
标准布朗运动是一个随机过程,其中它们的步长是从由零均值(μ=0)和单位方差(σ2=1)的正态(高斯)分布定义的概率函数中得出的。该运动在x点的支配可能密度函数(PDF)如下:

1.2 莱维运动
莱维飞行是一种随机行走类型,其步长由莱维分布(幂律尾)定义的概率函数确定:

其中xj是飞行长度,1<α≤2是幂律指数。积分形式的Lévy稳定过程的概率密度定义为:

其中,α定义分布指数并控制过程的标度特性,而γ选择标度单位。方程(3)中的积分在少数情况下具有解析解。当α等于2时,表示高斯分布,当α等于1时,表示柯西分布。方程(3)中积分的解通常只在x具有如下巨大值时才需要使用级数展开法:

其中 T 表示伽玛函数,其中对于整数α数,(1+α)等于α!
Mantegna(1994)提出了一种准确而快速的算法,用于生成Lévy稳定过程,其指数分布(α)的任意值范围为0.3和1.99。本研究使用Magneta方法来生成基于Lévy分布的随机数,具体如下:

其中x和y是两个正态分布变量,σx和σy的标准偏差如下:

在等式(6)中,σx的计算如下:

图4描绘了莱维和布朗分布及其在二维和三维空间中的轨迹。图图4(a)和图4(d)显示了莱维和布朗运动在一维视角下的分布。图4(b)和(e)分别说明了根据Lévy和Brownian的分布得出的它们的2D轨迹。最后,图4(c)和图4(f)说明了这些轨迹的3D版本。如相关图所示,从Lévy策略开始的行走主要以与长跳跃相关的小步来跟踪域,而与Lévys策略相比,布朗运动可以以更均匀和受控的步长覆盖域的区域。

基于图4所示的特性,莱维飞行和布朗运动都不足以单独有效地全局和局部搜索域。然而,它们的组合和每种策略的正确使用可以提供一个系统的探索者-开发者框架,该框架可以比每种策略本身更有效地工作。如图所示,莱维飞行主要与小步和偶尔的跳远有关。这一特性可以在优化文献中用作改进的搜索能力,与均匀随机搜索相比,优化文献显示出更有效的性能。该图表明,尽管莱维飞行由于步长较小而能够高效深入地搜索附近的邻域,并由于步长较长而能够探索域的其他区域,但它不能仅覆盖域的所有区域。另一方面,从图中可以清楚地观察到布朗运动的行走,可以追踪和探索遥远的区域
2.数学模型
2.1 MPA配方
与大多数元启发式方法类似,MPA是一种基于群体的方法,其中初始解决方案在搜索空间上均匀分布,作为第一次试验:

其中Xmin和Xmax是变量的下界和上界,rand是0到1范围内的均匀随机向量。
根据适者生存理论,据说自然界中的顶级捕食者在觅食方面更有天赋。因此,最适者解被指定为顶级捕食者,以构建一个矩阵,称为精英。这个矩阵的阵列根据猎物的位置信息监督搜索和寻找猎物。

其中XI代表顶级捕食者向量,它被复制n次以构建精英矩阵。n是搜索代理的数量,而d是维度的数量。值得注意的是,捕食者和猎物都被视为搜索主体。因为当捕食者在寻找猎物时,猎物正在寻找自己的食物。在每次迭代结束时,如果顶级捕食者被更好的捕食者取代,精英将被更新。
另一个与精英维度相同的矩阵被称为猎物,捕食者根据它更新自己的位置。简单地说,初始化创建了初始猎物,其中最适者(捕食者)构建了精英。Prey如下所示:

在式(11)中,Xi,j表示第i个猎物的第j个维度。需要注意的是,整个优化过程主要与这两个矩阵直接相关。
2.2 MPA优化场景
MPA优化过程分为三个主要的优化阶段,考虑到不同的速度比,同时模拟捕食者和猎物的整个生命:(1)在高速度比下或当猎物比捕食者移动得更快时,(2)在单位速度比下,或当捕食者和猎物以几乎相同的速度移动时,以及(3)在低速比下,当捕食者比猎物移动得更快时。对于每个定义的阶段,都会指定并分配一个特定的迭代周期。这些步骤是基于捕食者和猎物运动性质的规则定义的,同时模仿自然界中捕食者和猎物的运动。这三个阶段包括:
阶段1:在高速度比下,或者当捕食者比猎物移动得更快时。这种情况发生在优化的初始迭代中,探索很重要。基于从图1中提取的规则。在高速比(v≥10)下,捕食者的最佳策略是完全不移动。该规则的数学模型应用为:

其中RB是包含基于表示布朗运动的正态分布的随机数的向量。该表示法显示按条目的乘法运算。RB与猎物的乘积模拟了猎物的运动。P=0.5是一个常数,R是[0,1]中均匀随机数的向量。这种情况发生在迭代的前三分之一,当步长或移动速度对于高探索能力来说很高时。Iter是当前迭代,而Max_Iter是最大迭代。
阶段2:在单位速度比内,或者当捕食者和猎物以相同的速度移动时。它模仿了它们都在寻找猎物。本节发生在优化的中间阶段,在该阶段,勘探试图暂时转换为开发。在这个阶段,勘探和开采都很重要。因此,一半的人口被指定用于勘探,另一半被指定用于开发。在这个阶段,猎物负责开发,捕食者负责探索。根据该规则,在单位速度比(v≈1)下,如果猎物在莱维方向移动,则捕食者的最佳策略是布朗策略。因此,本研究考虑了猎物在莱维运动,而捕食者在布朗运动。

其中RL是基于代表莱维运动的莱维分布的随机数的向量。RL和Prey的乘积以Lévy方式模拟猎物的运动,而将步长添加到猎物位置则模拟猎物的移动。由于大多数Levy分布步长与小步长有关,因此本节有助于开发。对于后半部分人口,本研究假设:

阶段3:在低速比或捕食者比猎物移动得更快的情况下。这种情况发生在优化过程的最后阶段,这主要与高开发能力有关。在低速比(v=0.1)下,捕食者的最佳策略是莱维。本阶段内容如下:

这项研究根据从不同文献中提取的规则和要点,按照自然界中发生的情况,模拟捕食者和猎物的运动。这些阶段模拟了捕食者捕捉猎物的步骤大小。根据这些规则,在捕食者的一生中假设相同比例的Lévy和布朗运动是合理的。在第一阶段,捕食者根本没有移动,而在第二阶段,它在布朗运动,最后在第三阶段,它显示出Lévy策略。这种情况也发生在猎物身上,因为猎物是另一种潜在的捕食者,例如:丝鲨和金枪鱼。它们都被认为是海洋捕食者,但金枪鱼是丝鲨的猎物,而它是多骨鱼类和海洋无脊椎动物的捕食者。在第一阶段,猎物以布朗式运动,在第二阶段,它遵循莱维行为。实验表明,将三分之一的迭代分配给每个阶段的策略是最优化的,与在这些阶段之间切换或循环重复阶段的策略相比,它的结果略好。由于这是该方法的第一个版本,感兴趣的读者可以通过定义算法如何以及何时使用每个阶段进行更新的其他标准来改进该方法。
2.3 涡流形成与FAD效应
导致海洋捕食者行为变化的另一点是环境问题,如涡流形成或鱼类聚集装置(FAD)效应。鲨鱼80%以上的时间都在FAD附近,其余20%的时间,它们将在不同的维度上进行更长的跳跃,可能是为了找到另一个猎物分布的环境。FAD被认为是局部最优,它们的作用是在搜索空间中捕获这些点。在模拟过程中考虑这些较长的跳跃避免了局部最优的停滞。因此,FADs效应在数学上表示为:

3.文件结构

func_plot.m % 绘图函数
Get_Functions_details.m % 基准的全部信息和实现
initialization.m % 初始化
levy.m % 莱维运动方程
main.m % 主函数
MPA.m % 海洋捕食者算法
4.伪代码

5.详细代码及注释
5.1 func_plot.m
function func_plot(func_name)
[lb,ub,dim,fobj]=Get_Functions_details(func_name);
switch func_name
case 'F1'
x=-100:2:100; y=x; %[-100,100]
case 'F2'
x=-100:2:100; y=x; %[-10,10]
case 'F3'
x=-100:2:100; y=x; %[-100,100]
case 'F4'
x=-100:2:100; y=x; %[-100,100]
case 'F5'
x=-200:2:200; y=x; %[-5,5]
case 'F6'
x=-100:2:100; y=x; %[-100,100]
case 'F7'
x=-1:0.03:1; y=x %[-1,1]
case 'F8'
x=-500:10:500;y=x; %[-500,500]
case 'F9'
x=-5:0.1:5; y=x; %[-5,5]
case 'F10'
x=-20:0.5:20; y=x;%[-500,500]
case 'F11'
x=-500:10:500; y=x;%[-0.5,0.5]
case 'F12'
x=-10:0.1:10; y=x;%[-pi,pi]
case 'F13'
x=-5:0.08:5; y=x;%[-3,1]
case 'F14'
x=-100:2:100; y=x;%[-100,100]
case 'F15'
x=-5:0.1:5; y=x;%[-5,5]
case 'F16'
x=-1:0.01:1; y=x;%[-5,5]
case 'F17'
x=-5:0.1:5; y=x;%[-5,5]
case 'F18'
x=-5:0.06:5; y=x;%[-5,5]
case 'F19'
x=-5:0.1:5; y=x;%[-5,5]
case 'F20'
x=-5:0.1:5; y=x;%[-5,5]
case 'F21'
x=-5:0.1:5; y=x;%[-5,5]
case 'F22'
x=-5:0.1:5; y=x;%[-5,5]
case 'F23'
x=-5:0.1:5; y=x;%[-5,5]
end
L=length(x);
f=[];
for i=1:L
for j=1:L
if strcmp(func_name,'F15')==0 && strcmp(func_name,'F19')==0 && strcmp(func_name,'F20')==0 && strcmp(func_name,'F21')==0 && strcmp(func_name,'F22')==0 && strcmp(func_name,'F23')==0
f(i,j)=fobj([x(i),y(j)]);
end
if strcmp(func_name,'F15')==1
f(i,j)=fobj([x(i),y(j),0,0]);
end
if strcmp(func_name,'F19')==1
f(i,j)=fobj([x(i),y(j),0]);
end
if strcmp(func_name,'F20')==1
f(i,j)=fobj([x(i),y(j),0,0,0,0]);
end
if strcmp(func_name,'F21')==1 || strcmp(func_name,'F22')==1 ||strcmp(func_name,'F23')==1
f(i,j)=fobj([x(i),y(j),0,0]);
end
end
end
surfc(x,y,f,'LineStyle','none');
colormap winter
end
5.2 Get_Functions_details.m
function [lb,ub,dim,fobj] = Get_Functions_details(F)
switch F
case 'F1'
fobj = @F1;
lb=-100;
ub=100;
dim=50;
case 'F2'
fobj = @F2;
lb=-10;
ub=10;
dim=50;
case 'F3'
fobj = @F3;
lb=-100;
ub=100;
dim=50;
case 'F4'
fobj = @F4;
lb=-100;
ub=100;
dim=50;
case 'F5'
fobj = @F5;
lb=-30;
ub=30;
dim=50;
case 'F6'
fobj = @F6;
lb=-100;
ub=100;
dim=50;
case 'F7'
fobj = @F7;
lb=-1.28;
ub=1.28;
dim=50;
case 'F8'
fobj = @F8;
lb=-500;
ub=500;
dim=50;
case 'F9'
fobj = @F9;
lb=-5.12;
ub=5.12;
dim=50;
case 'F10'
fobj = @F10;
lb=-32;
ub=32;
dim=50;
case 'F11'
fobj = @F11;
lb=-600;
ub=600;
dim=50;
case 'F12'
fobj = @F12;
lb=-50;
ub=50;
dim=50;
case 'F13'
fobj = @F13;
lb=-50;
ub=50;
dim=50;
case 'F14'
fobj = @F14;
lb=-65.536;
ub=65.536;
dim=2;
case 'F15'
fobj = @F15;
lb=-5;
ub=5;
dim=4;
case 'F16'
fobj = @F16;
lb=-5;
ub=5;
dim=2;
case 'F17'
fobj = @F17;
lb=[-5,0];
ub=[10,15];
dim=2;
case 'F18'
fobj = @F18;
lb=-2;
ub=2;
dim=2;
case 'F19'
fobj = @F19;
lb=0;
ub=1;
dim=3;
case 'F20'
fobj = @F20;
lb=0;
ub=1;
dim=6;
case 'F21'
fobj = @F21;
lb=0;
ub=10;
dim=4;
case 'F22'
fobj = @F22;
lb=0;
ub=10;
dim=4;
case 'F23'
fobj = @F23;
lb=0;
ub=10;
dim=4;
end
end
% F1
function o = F1(x)
o=sum(x.^2);
end
% F2
function o = F2(x)
o=sum(abs(x))+prod(abs(x));
end
% F3
function o = F3(x)
dim=size(x,2);
o=0;
for i=1:dim
o=o+sum(x(1:i))^2;
end
end
% F4
function o = F4(x)
o=max(abs(x));
end
% F5
function o = F5(x)
dim=size(x,2);
o=sum(100*(x(2:dim)-(x(1:dim-1).^2)).^2+(x(1:dim-1)-1).^2);
end
% F6
function o = F6(x)
o=sum(abs((x+.5)).^2);
end
% F7
function o = F7(x)
dim=size(x,2);
o=sum([1:dim].*(x.^4))+rand;
end
% F8
function o = F8(x)
o=sum(-x.*sin(sqrt(abs(x))));
end
% F9
function o = F9(x)
dim=size(x,2);
o=sum(x.^2-10*cos(2*pi.*x))+10*dim;
end
% F10
function o = F10(x)
dim=size(x,2);
o=-20*exp(-.2*sqrt(sum(x.^2)/dim))-exp(sum(cos(2*pi.*x))/dim)+20+exp(1);
end
% F11
function o = F11(x)
dim=size(x,2);
o=sum(x.^2)/4000-prod(cos(x./sqrt([1:dim])))+1;
end
% F12
function o = F12(x)
dim=size(x,2);
o=(pi/dim)*(10*((sin(pi*(1+(x(1)+1)/4)))^2)+sum((((x(1:dim-1)+1)./4).^2).*...
(1+10.*((sin(pi.*(1+(x(2:dim)+1)./4)))).^2))+((x(dim)+1)/4)^2)+sum(Ufun(x,10,100,4));
end
% F13
function o = F13(x)
dim=size(x,2);
o=.1*((sin(3*pi*x(1)))^2+sum((x(1:dim-1)-1).^2.*(1+(sin(3.*pi.*x(2:dim))).^2))+...
((x(dim)-1)^2)*(1+(sin(2*pi*x(dim)))^2))+sum(Ufun(x,5,100,4));
end
% F14
function o = F14(x)
aS=[-32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32;,...
-32 -32 -32 -32 -32 -16 -16 -16 -16 -16 0 0 0 0 0 16 16 16 16 16 32 32 32 32 32];
for j=1:25
bS(j)=sum((x'-aS(:,j)).^6);
end
o=(1/500+sum(1./([1:25]+bS))).^(-1);
end
% F15
function o = F15(x)
aK=[.1957 .1947 .1735 .16 .0844 .0627 .0456 .0342 .0323 .0235 .0246];
bK=[.25 .5 1 2 4 6 8 10 12 14 16];bK=1./bK;
o=sum((aK-((x(1).*(bK.^2+x(2).*bK))./(bK.^2+x(3).*bK+x(4)))).^2);
end
% F16
function o = F16(x)
o=4*(x(1)^2)-2.1*(x(1)^4)+(x(1)^6)/3+x(1)*x(2)-4*(x(2)^2)+4*(x(2)^4);
end
% F17
function o = F17(x)
o=(x(2)-(x(1)^2)*5.1/(4*(pi^2))+5/pi*x(1)-6)^2+10*(1-1/(8*pi))*cos(x(1))+10;
end
% F18
function o = F18(x)
o=(1+(x(1)+x(2)+1)^2*(19-14*x(1)+3*(x(1)^2)-14*x(2)+6*x(1)*x(2)+3*x(2)^2))*...
(30+(2*x(1)-3*x(2))^2*(18-32*x(1)+12*(x(1)^2)+48*x(2)-36*x(1)*x(2)+27*(x(2)^2)));
end
% F19
function o = F19(x)
aH=[3 10 30;.1 10 35;3 10 30;.1 10 35];cH=[1 1.2 3 3.2];
pH=[.3689 .117 .2673;.4699 .4387 .747;.1091 .8732 .5547;.03815 .5743 .8828];
o=0;
for i=1:4
o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end
% F20
function o = F20(x)
aH=[10 3 17 3.5 1.7 8;.05 10 17 .1 8 14;3 3.5 1.7 10 17 8;17 8 .05 10 .1 14];
cH=[1 1.2 3 3.2];
pH=[.1312 .1696 .5569 .0124 .8283 .5886;.2329 .4135 .8307 .3736 .1004 .9991;...
.2348 .1415 .3522 .2883 .3047 .6650;.4047 .8828 .8732 .5743 .1091 .0381];
o=0;
for i=1:4
o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end
% F21
function o = F21(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:5
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
% F22
function o = F22(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:7
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
% F23
function o = F23(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:10
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
function o=Ufun(x,a,k,m)
o=k.*((x-a).^m).*(x>a)+k.*((-x-a).^m).*(x<(-a));
end
5.3 initialization.m
function Positions=initialization(SearchAgents_no,dim,ub,lb)
Boundary_no= size(ub,2); % numnber of boundaries
% If the boundaries of all variables are equal and user enter a signle
% number for both ub and lb
if Boundary_no==1
Positions=rand(SearchAgents_no,dim).*(ub-lb)+lb;
end
% If each variable has a different lb and ub
if Boundary_no>1
for i=1:dim
ub_i=ub(i);
lb_i=lb(i);
Positions(:,i)=rand(SearchAgents_no,1).*(ub_i-lb_i)+lb_i;
end
end
5.4 levy.m
function [z] = levy(n,m,beta)
num = gamma(1+beta)*sin(pi*beta/2); % used for Numerator
den = gamma((1+beta)/2)*beta*2^((beta-1)/2); % used for Denominator
sigma_u = (num/den)^(1/beta);% Standard deviation
u = random('Normal',0,sigma_u,n,m);
v = random('Normal',0,1,n,m);
z =u./(abs(v).^(1/beta));
end
5.5 main.m
clear all
clc
format long
SearchAgents_no=25; % Number of search agents
Function_name='F23';
Max_iteration=500; % Maximum number of iterations
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
[Best_score,Best_pos,Convergence_curve]=MPA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
% function topology
figure('Position',[500 400 700 290])
subplot(1,2,1);
func_plot(Function_name);
title('Function Topology')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])
% Convergence curve
subplot(1,2,2);
semilogy(Convergence_curve,'Color','r')
title('Objective space')
xlabel('Iteration');
ylabel('Best score obtained so far');
display(['The best solution obtained by MPA is : ', num2str(Best_pos,10)]);
display(['The best optimal value of the objective function found by MPA is : ', num2str(Best_score,10)]);
disp(sprintf('--------------------------------------'));
5.6 MPA.m
function [Top_predator_fit,Top_predator_pos,Convergence_curve]=MPA(SearchAgents_no,Max_iter,lb,ub,dim,fobj)
Top_predator_pos=zeros(1,dim);
Top_predator_fit=inf;
Convergence_curve=zeros(1,Max_iter);
stepsize=zeros(SearchAgents_no,dim);
fitness=inf(SearchAgents_no,1);
Prey=initialization(SearchAgents_no,dim,ub,lb);
Xmin=repmat(ones(1,dim).*lb,SearchAgents_no,1);
Xmax=repmat(ones(1,dim).*ub,SearchAgents_no,1);
Iter=0;
FADs=0.2;
P=0.5;
while Iter<Max_iter
%------------------- Detecting top predator -----------------
for i=1:size(Prey,1)
Flag4ub=Prey(i,:)>ub;
Flag4lb=Prey(i,:)<lb;
Prey(i,:)=(Prey(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
fitness(i,1)=fobj(Prey(i,:));
if fitness(i,1)<Top_predator_fit
Top_predator_fit=fitness(i,1);
Top_predator_pos=Prey(i,:);
end
end
%------------------- Marine Memory saving -------------------
if Iter==0
fit_old=fitness; Prey_old=Prey;
end
Inx=(fit_old<fitness);
Indx=repmat(Inx,1,dim);
Prey=Indx.*Prey_old+~Indx.*Prey;
fitness=Inx.*fit_old+~Inx.*fitness;
fit_old=fitness; Prey_old=Prey;
%------------------------------------------------------------
Elite=repmat(Top_predator_pos,SearchAgents_no,1); %(Eq. 10)
CF=(1-Iter/Max_iter)^(2*Iter/Max_iter);
RL=0.05*levy(SearchAgents_no,dim,1.5); %Levy random number vector
RB=randn(SearchAgents_no,dim); %Brownian random number vector
for i=1:size(Prey,1)
for j=1:size(Prey,2)
R=rand();
%------------------ Phase 1 (Eq.12) -------------------
if Iter<Max_iter/3
stepsize(i,j)=RB(i,j)*(Elite(i,j)-RB(i,j)*Prey(i,j));
Prey(i,j)=Prey(i,j)+P*R*stepsize(i,j);
%--------------- Phase 2 (Eqs. 13 & 14)----------------
elseif Iter>Max_iter/3 && Iter<2*Max_iter/3
if i>size(Prey,1)/2
stepsize(i,j)=RB(i,j)*(RB(i,j)*Elite(i,j)-Prey(i,j));
Prey(i,j)=Elite(i,j)+P*CF*stepsize(i,j);
else
stepsize(i,j)=RL(i,j)*(Elite(i,j)-RL(i,j)*Prey(i,j));
Prey(i,j)=Prey(i,j)+P*R*stepsize(i,j);
end
%----------------- Phase 3 (Eq. 15)-------------------
else
stepsize(i,j)=RL(i,j)*(RL(i,j)*Elite(i,j)-Prey(i,j));
Prey(i,j)=Elite(i,j)+P*CF*stepsize(i,j);
end
end
end
%------------------ Detecting top predator ------------------
for i=1:size(Prey,1)
Flag4ub=Prey(i,:)>ub;
Flag4lb=Prey(i,:)<lb;
Prey(i,:)=(Prey(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
fitness(i,1)=fobj(Prey(i,:));
if fitness(i,1)<Top_predator_fit
Top_predator_fit=fitness(i,1);
Top_predator_pos=Prey(i,:);
end
end
%---------------------- Marine Memory saving ----------------
if Iter==0
fit_old=fitness; Prey_old=Prey;
end
Inx=(fit_old<fitness);
Indx=repmat(Inx,1,dim);
Prey=Indx.*Prey_old+~Indx.*Prey;
fitness=Inx.*fit_old+~Inx.*fitness;
fit_old=fitness; Prey_old=Prey;
%---------- Eddy formation and FADs� effect (Eq 16) -----------
if rand()<FADs
U=rand(SearchAgents_no,dim)<FADs;
Prey=Prey+CF*((Xmin+rand(SearchAgents_no,dim).*(Xmax-Xmin)).*U);
else
r=rand(); Rs=size(Prey,1);
stepsize=(FADs*(1-r)+r)*(Prey(randperm(Rs),:)-Prey(randperm(Rs),:));
Prey=Prey+stepsize;
end
Iter=Iter+1;
Convergence_curve(Iter)=Top_predator_fit;
end
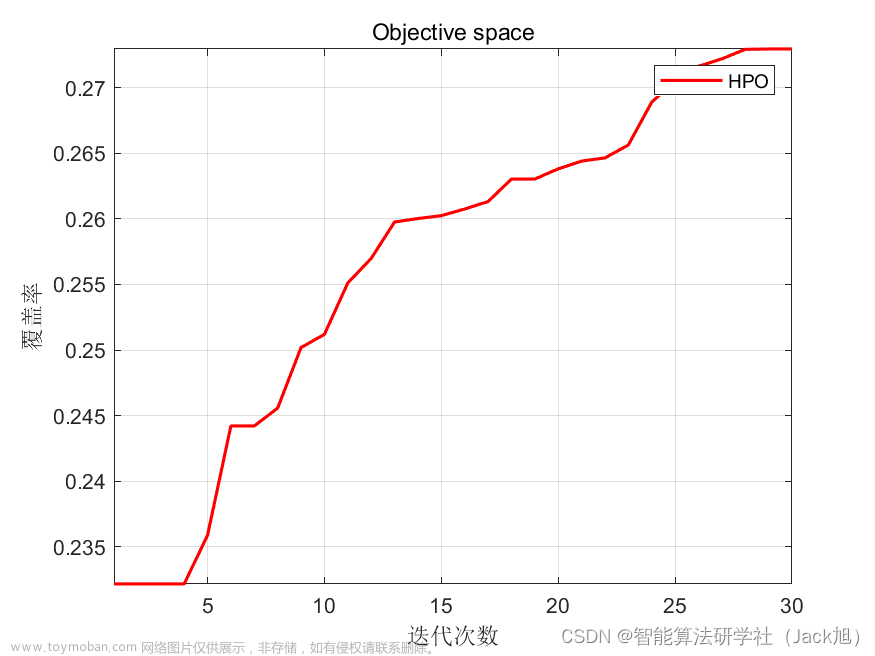
6.运行结果
 文章来源:https://www.toymoban.com/news/detail-534919.html
文章来源:https://www.toymoban.com/news/detail-534919.html
7.参考文献
[1]Faramarzi A,Heidarinejad M,Mirjalili S, et al. Marine Predators Algorithm: A nature-inspired metaheuristic[J]. Expert Systems With Applications,2020,152(prepublish).文章来源地址https://www.toymoban.com/news/detail-534919.html
到了这里,关于【Matlab】智能优化算法_海洋捕食者算法MPA的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!