目录
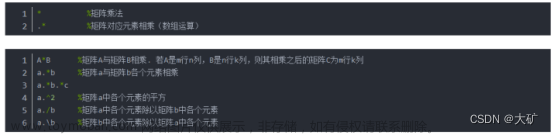
一、矩阵的加减运算
二、矩阵的乘方运算
1.数与矩阵的乘法
2.矩阵与矩阵的乘法
三、矩阵的除法
四、矩阵的幂运算
五、矩阵元素的查找
六、矩阵元素的排序
七、矩阵元素的求和
八、矩阵元素的求积
九、矩阵元素的差分
一、矩阵的加减运算
进行矩阵加法、减法运算的前提是参与运算的两个矩阵或多个矩阵必须具有相同的行数和列数,即A、B、C等多个矩阵均为m×n矩阵;或者其中有一个或多个矩阵为标量。
由于矩阵的加法运算归结为其元素的加法运算,容易验证,因此矩阵的加法运算满足下列运算律:
(1)交换律:A+B=B+A。
(2)结合律:A+(B+C)=(A+B)+C。
(3)存在零元:A+0=0+A=A。
(4)存在负元:A+(-A)=(-A)+A。
示例1:创建矩阵A,B;行向量C;标量X;试求A+B、A-B、A+B+x、A-x、A-C
A=[1 1 1 1;1 2 3 4;1 3 5 7;2 4 6 8];
B=[1 1 1 1;1 2 3 4;1 3 5 7;2 4 6 8];
C=[1 2];
X=2;
D=A+B
E=A-B
F=A+B+X
G=A-X
H=A-C运行结果:

二、矩阵的乘方运算
MATLAB中矩阵的乘法运算包括两种:数与矩阵的乘法;矩阵与矩阵的乘法。
1.数与矩阵的乘法
示例2:矩阵数乘
A=[1 1 1;1 3 5;2 4 6];
E=eye(3); %3维的单位矩阵
C=2*A+3*E运行结果:

2.矩阵与矩阵的乘法
两个矩阵的乘法必须满足被乘矩阵的列数与乘矩阵的行数相等。
示例3:矩阵相乘
A=[1 3 5 7;2 4 6 8];
B=[1 1 1;1 2 3;1 3 5;2 4 6];
C=A*B
D=B*A运行结果:

三、矩阵的除法
矩阵的除法是乘法的逆运算,分为左除和右除两种,分别用运算符号“\”和“/”表示。
示例4:矩阵的除法
A=[1 2;1 3];
B=[1 0;1 2];
C=A\B %左除
D=B/A %右除运行结果:

注意:A\B表示矩阵A的逆乘以B,A/B表示矩阵A乘以矩阵B的逆。除非矩阵A和矩阵B相同,否则A/B和A\B是不等价的。对于一般的二维矩阵A和B,当进行A\B运算时,要求A的行数与B的行数相等;当进行A/B运算时,要求A的列数与B的列数相等。
四、矩阵的幂运算
当矩阵A为方阵时,可进行矩阵的幂运算。在MATLAB中,使用运算符号“^”表示幂运算。
示例5:方阵幂运算
A=[1 2;1 3];
B=A^2 % 平方
C=A^3 % 三次方运行结果:

五、矩阵元素的查找
MATLAB中函数find()的作用是进行矩阵元素的查找,它通常与关系函数和逻辑运算相结合。其调用格式如下:
- ind = find(X):该函数查找矩阵X中的非零元素,函数返回这些元素的单下标。
- [row,col] = find(X,...):该函数查找矩阵X中的非零元素,函数返回这些元素的双下标i和j。
示例6:利用函数find()查找矩阵中的元素
A=[1 2 0;1 3 0;2 4 6];
B=find(A) %矩阵中非零元素的下标
C=find(A>=1) %矩阵中大于等于1的元素的下标
D=A(A>=1) %矩阵中大于等于1的元素
E=[B C D]
A(find(A==0))=10 %矩阵中等于0的元素改为0运行结果:

六、矩阵元素的排序
MATLAB中函数sort()的作用是按照升序排序,排序后的矩阵和原矩阵的维数相同。其调用格式如下:
- B = sort(A):该函数对矩阵A进行升序排列。A可为矩阵或向量。
- B = sort(A,dim):该函数对矩阵 A 进行升序排列,并将结果返回在给定的维数dim上按照升序排列。当dim=1时,按照列进行排序;当dim=2时,按照行进行排序。
- B = sort(...,mode):该函数对矩阵A进行排序,mode可指定排序的方式。ascend指定按升序排列,为默认值;descend指定按降序排列。
示例7:矩阵元素的排序
A=[1 2 0;1 3 0;2 4 6];
B=sort(A) %矩阵中元素按照列进行升序排序
C=sort(A,2) %矩阵中元素按照行进行升序排序
D=sort(A,'descend') %矩阵中元素按照列进行降序排序
E=sort(A,2,'descend') %矩阵中元素按照行进行降序排序运行结果:

示例8:对向量进行排序
A=[5 8 1 6 9];
sort(A)运行结果:

七、矩阵元素的求和
MATLAB中函数sum()和cumsum()的作用是对矩阵的元素求和。其调用格式如下:
- B = sum(A):该函数对矩阵A的元素求和,返回由矩阵A各列元素的和组成的向量。
- B = sum(A,dim):该函数返回在给定的维数dim上元素的和。当dim=1时,计算矩阵A各列元素的和;当dim=2时,计算矩阵A各行元素的和。
- B = cumsum(A)。
- B = cumsum(A,dim)。
- 函数cumsum()的调用格式与sum()类似,不同的是其返回值为矩阵。下面通过示例查看两个函数的不同之处。
示例9:矩阵元素的求和
A=[1 2 0;1 3 0;2 4 6];
B=sum(A) %矩阵中元素按照列进行求和
C=sum(A,2) %矩阵中元素按照行进行求和
D=cumsum(A) %矩阵中各列元素求和
E=cumsum(A,2) %矩阵中各行元素求和
F=sum(sum(A)) %矩阵中所有元素的和运行结果:

八、矩阵元素的求积
MATLAB中函数prod()和cumprod()的作用是对矩阵的元素求积。其调用格式如下:
- B = prod(A):该函数对矩阵A的元素求积,返回由矩阵A各列元素的积组成的向量。
- B = prod(A,dim):该函数返回在给定的维数dim上元素的积。当dim=1时,计算矩阵A各列元素的积;当dim=2时,计算矩阵A各行元素的积。
- B = cumprod(A)。
- B = cumprod(A,dim)。
- 函数 cumprod()的调用格式与 prod()类似,不同的是其返回值为矩阵。读者可以通过下面的示例查看两者的不同之处。
示例10:矩阵元素的求积
A=[1 2 0;1 3 0;2 4 6];
B=prod(A) %矩阵中各列元素的积
C=prod(A,2) %矩阵中各行元素的积
D=cumprod(A) %矩阵中各列元素的积
E=cumprod(A,2) %矩阵中各行元素的积运行结果:

九、矩阵元素的差分
MATLAB中函数diff()的作用是计算矩阵的差分。其调用格式如下:
- Y = diff(X):计算矩阵各列元素的差分。
- Y = diff(X,n):计算矩阵各列元素的n阶差分。
- Y = diff(X,n,dim):计算矩阵在给定的维数dim上元素的n阶差分。当dim=1时,计算矩阵各列元素的差分;当dim=2时,计算矩阵各行元素的差分。
示例11:矩阵元素的差分
A=[1 2 0;1 3 0;2 4 6];
B=diff(A) %矩阵中各列元素的差分
C=diff(A,2) %矩阵中各列元素的2阶差分
D=diff(A,1,1) %矩阵中各列元素的差分
E=diff(A,1,2) %矩阵中各行元素的差分运行结果:
 文章来源:https://www.toymoban.com/news/detail-535145.html
文章来源:https://www.toymoban.com/news/detail-535145.html
注意:当参数n≥size(x,dim)时,函数的返回值是空矩阵。文章来源地址https://www.toymoban.com/news/detail-535145.html
到了这里,关于9、矩阵的简单运算的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!