一、矩阵分块法介绍
概念：
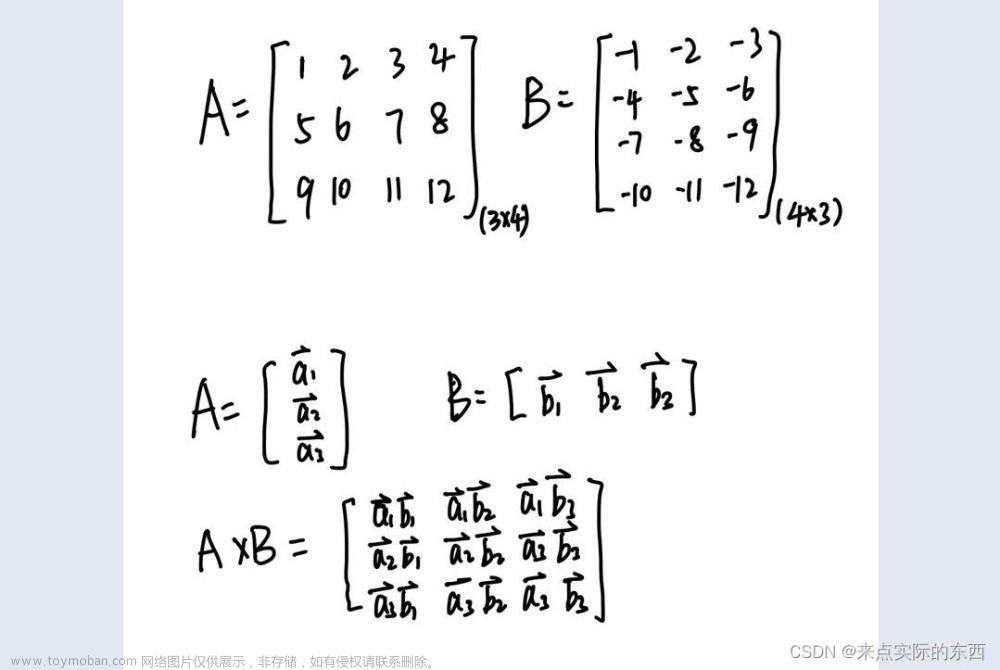
例：
二、使用矩阵分块法计算矩阵的积
1. 分块矩阵计算的数学步骤
- 使用Numpy计算例1
import numpy as np
A=np.mat([[1,0,0,0],[0,1,0,0],[-1,2,1,0],[1,1,0,1]])
B=np.mat([[1,0,1,0],[-1,2,0,1],[1,0,4,1],[-1,-1,2,0]])
A*B
文章来源：https://www.toymoban.com/news/detail-535303.html
三、按行分块和按列分块
- 按列分块
- 按行分块
- 分块后的计算公式
四、矩阵分块与线性方程组
文章来源地址https://www.toymoban.com/news/detail-535303.html
五、矩阵分块法总结
- 矩阵分块法提供了行数和列数较多的矩阵相乘的一种计算方法，以此来简化矩阵相乘的运算次数；
- 按行列分块将矩阵A分为n个列向量和m个行向量，利用矩阵乘法的定义，殊途同归，推导出了矩阵相乘的公式，从分块的角度来理解矩阵相乘的定义；
- 矩阵分块再一次推广了线性方程组的定义范围，对于含有n个未知数和m个线性方程组的解答思路和各种变形；
到了这里，关于【线性代数】从矩阵分块的角度理解矩阵乘法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
