一、Kruskal算法
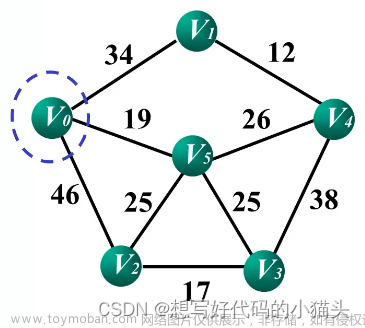
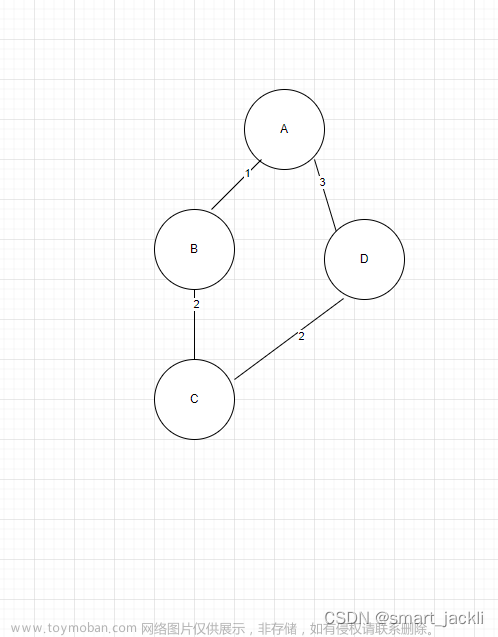
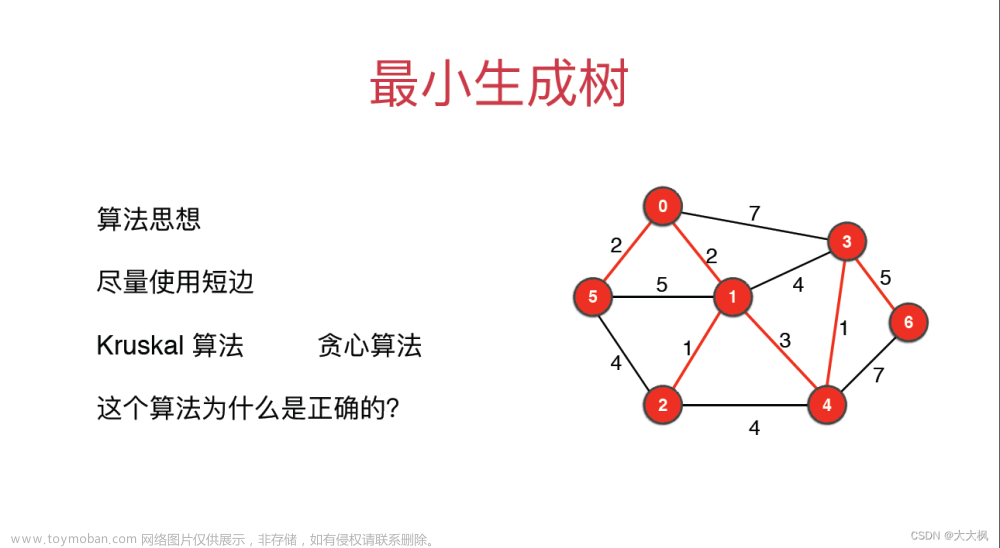
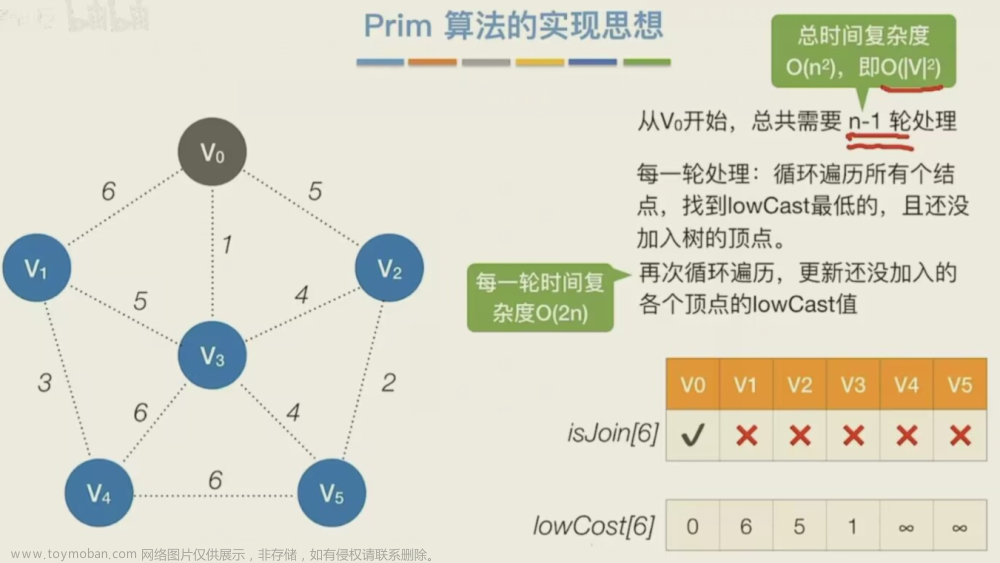
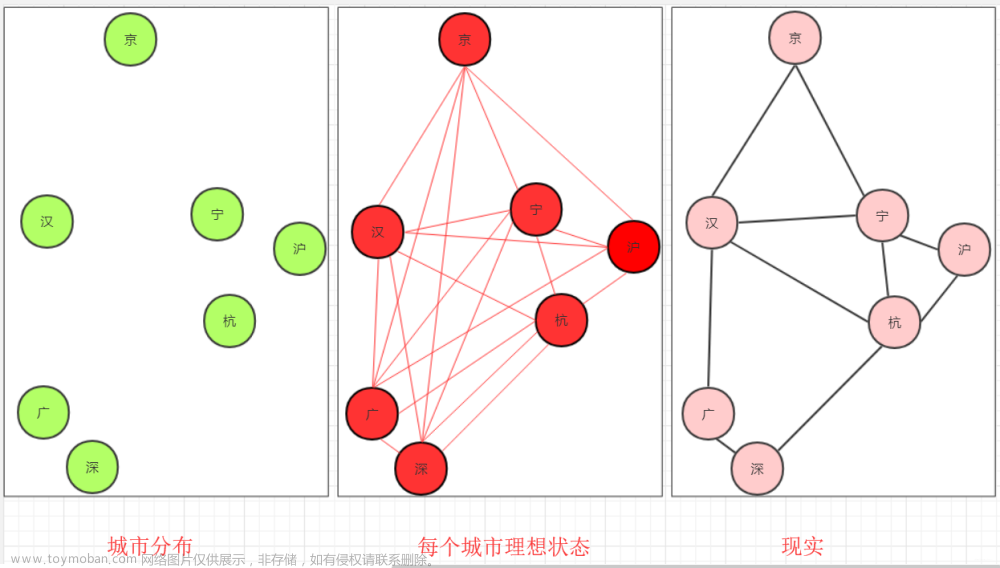
克鲁斯卡尔算法(Kruskal)是一种使用贪婪方法的最小生成树算法。 该算法初始将图视为森林,图中的每一个顶点视为一棵单独的树。 一棵树只与它的邻接顶点中权值最小且不违反最小生成树属性(不构成环)的树之间建立连边。
二、具体效果

文章来源:https://www.toymoban.com/news/detail-535815.html
最小生成树法生成网络文章来源地址https://www.toymoban.com/news/detail-535815.html
三、代码
clc
clear
close all
P=[20,100;3,31;83,44;93,19;77,14;85,44;18,35;84,39;18,49;37,46;9,86;46,85;68,40;9,5;45,15;23,89;5,40;44,61;72,50;46,68];
%计算距离矩阵
D=inf*ones(size(P,1),size(P,1));
for i=1:size(P,1)-1
for j=i+1:size(P,1)
D(i,j)=norm(P(i,:)-P(j,:));
end
end
plot(P(:,1),P(:,2),'.k','MarkerSize',20)
hold on
%Kruskal算法
temp=[]; %已经选择的节点
while size(unique(temp),1)<size(P,1)
%寻找最短的边
[xx,yy]=find(D==min(min(D)));
ii=xx(1);
jj=yy(1);
%判断ii和jj加进去是否成环
io=judge(P,temp,ii,jj);
if io==0
temp=[temp;ii,jj];
plot([P(ii,1),P(jj,1)],[P(ii,2),P(jj,2)],'-b')
hold on
pause(0.1)
end
D(ii,jj)=inf;
end
到了这里,关于最小生成树matlab代码Kruskal算法,用于二维网络生成的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!