力扣题目:#518.零钱兑换II(完全背包组合问题)
刷题时长:7min
解题方法:动态规划(完全背包)
复杂度分析
- 时间复杂度: O(mn),其中 m 是amount,n 是 coins 的长度
- 空间复杂度: O(m)
问题总结文章来源:https://www.toymoban.com/news/detail-535869.html
- 对递推公式的理解
本题收获文章来源地址https://www.toymoban.com/news/detail-535869.html
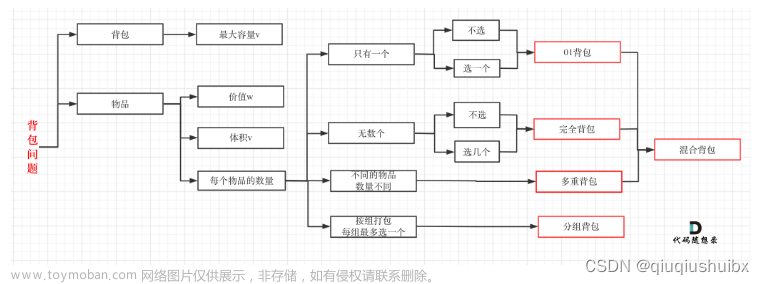
- 题意转换:纯完全背包是凑成背包最大价值是多少,而本题是要求凑成总金额的物品组合个数
- 动规思路
- 确定dp数组及下标的含义:凑成总金额j的货币组合数为dp[j]
- 确定递推公式:dp[j] += dp[j - coins[i]]
- 反向思考递推,当有coins[i]时,就有dp[j-coins]种方法,因为此时凑成目标和的方法解即为j+coins[i],而方法数量不变
- dp数组的初始化:dp[0] = 1
- 确定遍历顺序:求组合,遍历必须先物品(coins),再背包(amount)
力扣题目:#377.组合总和Ⅳ(完全背包排列问题)
刷题时长:7min
解题方法:动态规划(完全背包)
复杂度分析
- 时间复杂度: O(target * n),其中 n 为 nums 的长度
- 空间复杂度: O(target)
问题总结
- 题目要求的combination其实是排列数,需要仔细看sample
- 先背包的遍历顺序需要加条件判断,先物品再背包不需要是因为写在循环index的边界值里了
本题收获
- 动规思路
- 确定dp数组及下标的含义:凑成目标正整数为i的排列个数为dp[i]
- 确定递推公式:dp[i] += dp[i - nums[j]]
- dp数组的初始化:dp[0] = 1
- 确定遍历顺序:求排列数就是外层for遍历背包,内层for循环遍历物品
到了这里,关于力扣算法刷题Day44|动态规划:完全背包问题 零钱兑换II 组合总和Ⅳ的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!