图论＋线性规划建模——蔬菜供应方案

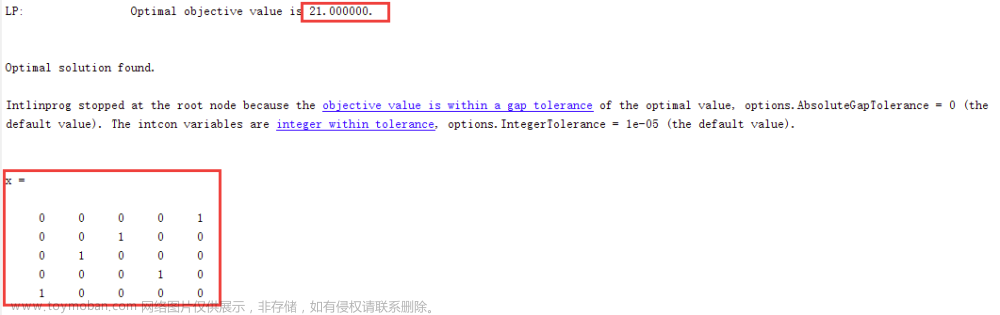
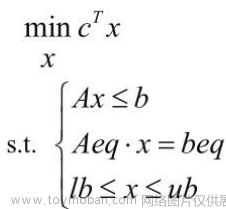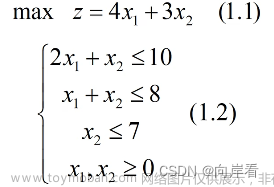记录一下学校训练的一道建模题目

1问题描述

江平市是一个人口不到20万人的小城市。根据该市的蔬菜种植情况，分别在菜市场（A），城乡路口（B）和南街口（C）设三个收购点，再由各收购点分送到全市的8个菜市场，该市道路情况，各路段距离（单位：100m）及各收购点，菜市场①到⑧的具体位置见下图。

按常年情况，A、B、C三个收购点每天收购量分别为250，200和180（单位：100 kg）,各菜市场的每天需求量及发生供应短缺时带来的损失（元/100kg）见表1。

设从收购点至各菜市场蔬菜调运费为2元/(100kg.100m)。试解决以下问题：

1. 为该市设计一个从收购点至个菜市场的定点供应方案，使用于蔬菜调运及预期的短缺损失为最小；
2. 若规定各菜市场短缺量一律不超过需求量的25%，重新设计定点供应方案；
3. 为满足城市居民的蔬菜供应，该市的领导规划增加蔬菜种植面积，试问增产的蔬菜每天应分别向A、B、C三个采购点供应多少最经济合理。

2问题分析

问题一分析

问题一的建模目的是设计一个从收购点至菜市场的定点供应方案，使用于蔬菜调运及预期的短缺损失为最小。首先，问题给出了3个收购点，每天的收购量分别为250，200和180（单位：100 kg）。其次，问题给出了8个菜市场，从收购点到菜市场的蔬菜调运费为2元/(100kg.100m)，每一个收购点到菜市场都有多条可供选择的运输路线，为了使蔬菜调运的损失最小，我们需要设计一个最佳的调运方案。最后，问题给出了8个菜市场每天的需求量和发生供应短缺时带来的损失，为了使供应短缺损失最小，我们需要设计一个最佳的供应方案。

因此，在设计蔬菜供应方案时，要分成两个子问题考虑。

1. 最小调运损失：蔬菜要从3个收购点调运到8个菜市场，路段距离已经给出。可以很容易地想出，由于调运费是统一的2元，所以3个收购点到8个菜市场的24条最短路径就是最佳调运方案，可知最小调运损失=最短路径×调运数量×调运费。其中只有调运数量是未知的。
2. 最小短缺损失：8个菜市场每天的总需求为700，而3个收购点每天的总收购量才630，这就意味着必然会发生短缺。可知最小短缺损失=短缺数量×单位短缺损失。其中只有短缺数量是未知的，而短缺数量=需求量-调运数量，所以最终问题依旧是求解调运数量。

因此最小总损失=最小调运损失+最小短缺损失。我们的目的就是通过建立模型求得最短路径和调运数量，得到的总体最小损失对应的路径和调运数量就是最佳供应方案。

问题二分析

问题二的建模目的是在各菜市场短缺量一律不超过需求量的25%的前提条件下，设计一个从收购点至菜市场的定点供应方案，使用于蔬菜调运及预期的短缺损失为最小。经过分析可知，问题二是在问题一的基础上增加了一个约束条件。

增加的约束条件为：各菜市场的供应量不得低于需求量的75%。

问题三分析

问题三的建模目的是为满足菜市场的蔬菜供应需求，要增产蔬菜以弥补供应短缺，设计一个收购点的增产蔬菜供应方案，使得蔬菜向菜市场供应最经济合理。经过分析可知，问题三是在问题一的基础上，增加了一个约束条件，并修改了一个约束条件。

增加的约束条件为：为了满足菜市场的蔬菜供应需求，收购点的总收购量必须不小于菜市场的总需求量。修改的约束条件为：每个菜市场的供应量不再是不大于需求量，而是必须等于需求量。

3问题假设

假设1：设1单位蔬菜为100kg，1单位路程为100m。

假设2：从收购点到菜市场的调运损失只与距离有关，与运输工具和运输费用无关。即一单位路程和一单位蔬菜的运输费用为2元。

其余假设待补充。。。

4建模与求解

变量说明

问题一

建模

根据题中所给数据，可以先计算出从收购点$S_i$到菜市场$A_j$的最小调运损失$c_{ij}$，再根据$c_{ij}$和调运的蔬菜数量$x_{ij}$以及各菜市场的短缺损失建立数学规划模型，求解最小短缺损失，得到最佳的调运方案。需要注意的是，虽然可以把问题分解成两个子问题进行处理，但最终优化时，必须作为一个综合的优化问题进行处理，否则无法得到全局最优解。

1. 最小调运损失
   首先构造蔬菜供应网点赋权无向图G =（V，E，W），其中V = {S1, S2, S3, A1,…,A8, B1,…,B4}={v1, …, v15}，总共15个顶点，W = (${\omega }_{ij}$)15×15。
   $${\omega }_{ij}=\{\begin{array}{rlr}{d}_{ij}& ,& v_i,v_j之间有路直接相连\\ +\infty & ,& v_i,v_j之间没有路直接相连\end{array}$$
   式中$d_{ij}$为$v_i,v_j$之间的路程，单位为100m。然后应用Dijkstra算法求得任意两点间的最短路径，并提取需要的收购点$S_i,(i=1,2,3)$到$A_j,(j=1,2,...,8)$菜市场的最短路径$c_{ij}$，组成3×8的最短路径矩阵c。由c可得从收购点到菜市场的1单位蔬菜的最小调运损失，由x可得从收购点到菜市场调运的蔬菜数量，二者累乘得总的最小调运损失。下一步我们要建立总损失的数学规划模型，将x求解出来。
2. 总损失的数学规划模型
   a.目标函数
   从收购点到菜市场的1单位蔬菜的最小调运损失为
   $$\sum _{i=1}^3\sum _{j=1}^{8}2c_{ij}{x}_{ij}$$
   总损失不仅要考虑运输带来的调运损失，还要考虑由于蔬菜缺乏造成的损失。经过分析可知，如果菜市场得到的蔬菜小于需求，则损失为单位短缺的损失与短缺的数量之积。菜市场 j 由于蔬菜缺乏造成的最小短缺损失为
   $$m_j=z_j(y_j-\sum _{i=1}^3{x}_{ij})$$
   因而，总损失为最小调运损失+最小短缺损失
   $$\sum _{i=1}^3\sum _{j=1}^{8}2c_{ij}{x}_{ij}+\sum _{j=1}^8{m}_j$$
   b.约束条件
   所有菜市场调运的蔬菜总量应该与所有收购点的总收购量相等
   $$\sum _{i=1}^3\sum _{j=1}^8{x}_{ij}=\sum _{i=1}^3{p}_i$$
   每个菜市场调运的蔬菜总量不大于菜市场的每日需求
   $$\sum _{i=1}^3{x}_{ij}\le \sum _{j=1}^8{y}_j,j=1,2,...,8$$
   所有菜市场从一个收购点调运的蔬菜总量应该与收购点的每日收购量相等
   $$\sum _{j=1}^8{x}_{ij}=p_i,i=1,2,3$$
   非负约束
   $$x_{ij}\ge 0,i=1,2,3,j=1,2,...,8$$

代码

clc, clear
% 蔬菜供应方案设计
% 自定义15个顶点名称
NN1 = strcat('S',cellstr(int2str([1:3]')));
NN2 = strcat('A',strtrim(cellstr((int2str([1:8]')))));
NN3 = strcat('B',strtrim(cellstr(int2str([1:4]'))));
NN=[NN1(:)',NN2(:)',NN3(:)'];
% 构建无向图G，图中有15个顶点,30条边
G = graph; G = addnode(G,NN);
L1 = {'S1','A1',4;'S1','A2',8;'S1','A6',6;'S1','B1',7;'S1','B2',4
'S2','A2',7;'S2','A3',7;'S2','B1',6;'S2','B4',11;'S3','A5',6
'S3','A7',5;'S3','A8',10;'S3','B3',8;'A1','A2',7;'A1','A6',5
'A2','B1',3;'A3','S1',8;'A3','A5',5;'A3','B1',5;'A3','B2',4
'A3','B4',6;'A4','B4',5;'A5','B2',7;'A5','B3',6;'A5','B4',3
'A6','B2',5;'A6','B3',7;'A7','A8',11;'A7','B3',10;'A8','B4',6};
G = addedge(G,L1(:,1),L1(:,2), cell2mat(L1(:,3)));
% 求所有点对之间的最短路径，返回一个15×15的矩阵
d = distances(G);
writematrix(d,'data2_1.xlsx')
% 根据最短路径求所有点对的最小运费
c1 = inf*ones(size(d));
c1(d==0)=0; 
ind=(d>0);
c1(ind)=2*ceil(d(ind));
writematrix(c1,'data2_1.xlsx','Sheet', 2)
% 提出3行8列的运费数据，即收购点S到菜市场A的1单位蔬菜的最小运费数据
c = c1(1:3,4:11); 
writematrix(c,'data2_1.xlsx','Sheet', 3)
h=plot(G,'EdgeLabel',G.Edges.Weight,'Layout', 'auto','NodeFontSize',12,'EdgeColor','k');

% y为菜市场每天需求，z为菜市场短缺1单位蔬菜的损失，p为收购点每天的收购量
y = [80, 70, 90, 80, 120, 70, 100, 90];
z = [10, 8, 5, 10, 10, 8, 5, 8];
p = [250, 200, 180]';

prob = optimproblem;
% 要求解的变量x
x = optimvar('x',3,8, 'LowerBound',0);
% 要求解的目标函数
obj = sum(sum(c.*x))+sum(z.*(y-sum(x)));
prob.Objective = obj;
% 约束条件
prob.Constraints.con1 = sum(sum(x))==sum(p);
prob.Constraints.con2 = sum(x) <= y;
prob.Constraints.con3 = sum(x,2) == p;
% 调用solve工具箱求解
[sol, fval, flag, out] = solve(prob)
% 输出最小损失
fval
% 输出方案x
sol.x
writematrix(sol.x,'data2_1.xlsx','Sheet', 4)

求解

利用MATLAB软件对上述模型进行求解，从计算结果得知，求得总损失的最小值为10280元。具体的1单位蔬菜的最小运输费用如下表所示

具体的最佳供应方案如下表所示

问题二

建模

问题二在问题一的基础上增加了一个约束条件，即规定各菜市场供应量一律不低于需求量的75%
$$\sum _{i=1}^3{x}_{ij}\ge 0.75y_j,j=1,2,...,8$$

代码

clc, clear
% 蔬菜供应方案设计
% 自定义15个顶点名称
NN1 = strcat('S',cellstr(int2str([1:3]')));
NN2 = strcat('A',strtrim(cellstr((int2str([1:8]')))));
NN3 = strcat('B',strtrim(cellstr(int2str([1:4]'))));
NN=[NN1(:)',NN2(:)',NN3(:)'];
% 构建无向图G，图中有15个顶点,30条边
G = graph; G = addnode(G,NN);
L1 = {'S1','A1',4;'S1','A2',8;'S1','A6',6;'S1','B1',7;'S1','B2',4
'S2','A2',7;'S2','A3',7;'S2','B1',6;'S2','B4',11;'S3','A5',6
'S3','A7',5;'S3','A8',10;'S3','B3',8;'A1','A2',7;'A1','A6',5
'A2','B1',3;'A3','S1',8;'A3','A5',5;'A3','B1',5;'A3','B2',4
'A3','B4',6;'A4','B4',5;'A5','B2',7;'A5','B3',6;'A5','B4',3
'A6','B2',5;'A6','B3',7;'A7','A8',11;'A7','B3',10;'A8','B4',6};
G = addedge(G,L1(:,1),L1(:,2), cell2mat(L1(:,3)));
% 求所有点对之间的最短路径，返回一个15×15的矩阵
d = distances(G);
writematrix(d,'data2_1.xlsx')
% 根据最短路径求所有点对的最小运费
c1 = inf*ones(size(d));
c1(d==0)=0; 
ind=(d>0);
c1(ind)=2*ceil(d(ind));
writematrix(c1,'data2_1.xlsx','Sheet', 2)
% 提出3行8列的运费数据，即收购点S到菜市场A的1单位蔬菜的最小运费数据
c = c1(1:3,4:11); 
writematrix(c,'data2_1.xlsx','Sheet', 3)
h=plot(G,'EdgeLabel',G.Edges.Weight,'Layout', 'auto','NodeFontSize',12,'EdgeColor','k');
%highlight(h,c,'LineWidth',2,'LineStyle','-') %最短路径虚线加粗

% y为菜市场每天需求，z为菜市场短缺1单位蔬菜的损失，p为收购点每天的收购量
y = [80, 70, 90, 80, 120, 70, 100, 90];
z = [10, 8, 5, 10, 10, 8, 5, 8];
p = [250, 200, 180]';

prob = optimproblem;
x = optimvar('x',3,8, 'LowerBound',0);
obj = sum(sum(c.*x))+sum(z.*(y-sum(x)));
prob.Objective = obj;
% 约束条件
prob.Constraints.con1 = sum(sum(x))==sum(p);
prob.Constraints.con2 = sum(x) <= y;
prob.Constraints.con3 = sum(x,2) == p;
prob.Constraints.con4 = sum(x) >= y*0.75;
[sol, fval, flag, out] = solve(prob)
fval
sol.x
writematrix(sol.x,'data2_1.xlsx','Sheet', 4)

求解

利用MATLAB软件对上述模型进行求解，从计算结果得知，求得问题二的总损失的最小值为10520元。最佳调运路线不变，具体的问题二的最佳供应方案如下表

问题三

建模

问题三是在问题一的基础上，增加了一个约束条件，并修改了一个约束条件。
增加的约束条件为：为了满足菜市场的蔬菜供应需求，收购点的总收购量必须不小于菜市场的总需求量
$$\sum _{i=1}^3{p}_i\ge \sum _{j=1}^8{y}_j$$
修改的约束条件为：每个菜市场的供应量不再是不大于需求量，而是必须等于需求量
$$\sum _{i=1}^3{x}_{ij}=\sum _{j=1}^8{y}_j,j=1,2,...,8$$

代码

clc, clear
% 蔬菜供应方案设计
% 自定义15个顶点名称
NN1 = strcat('S',cellstr(int2str([1:3]')));
NN2 = strcat('A',strtrim(cellstr((int2str([1:8]')))));
NN3 = strcat('B',strtrim(cellstr(int2str([1:4]'))));
NN=[NN1(:)',NN2(:)',NN3(:)'];
% 构建无向图G，图中有15个顶点,30条边
G = graph; G = addnode(G,NN);
L1 = {'S1','A1',4;'S1','A2',8;'S1','A6',6;'S1','B1',7;'S1','B2',4
'S2','A2',7;'S2','A3',7;'S2','B1',6;'S2','B4',11;'S3','A5',6
'S3','A7',5;'S3','A8',10;'S3','B3',8;'A1','A2',7;'A1','A6',5
'A2','B1',3;'A3','S1',8;'A3','A5',5;'A3','B1',5;'A3','B2',4
'A3','B4',6;'A4','B4',5;'A5','B2',7;'A5','B3',6;'A5','B4',3
'A6','B2',5;'A6','B3',7;'A7','A8',11;'A7','B3',10;'A8','B4',6};
G = addedge(G,L1(:,1),L1(:,2), cell2mat(L1(:,3)));
% 求所有点对之间的最短路径，返回一个15×15的矩阵
d = distances(G);
writematrix(d,'data2_1.xlsx')
% 根据最短路径求所有点对的最小运费
c1 = inf*ones(size(d));
c1(d==0)=0; 
ind=(d>0);
c1(ind)=2*ceil(d(ind));
writematrix(c1,'data2_1.xlsx','Sheet', 2)
% 提出3行8列的运费数据，即收购点S到菜市场A的1单位蔬菜的最小运费数据
c = c1(1:3,4:11); 
writematrix(c,'data2_1.xlsx','Sheet', 3)
h=plot(G,'EdgeLabel',G.Edges.Weight,'Layout', 'auto','NodeFontSize',12,'EdgeColor','k');
%highlight(h,c,'LineWidth',2,'LineStyle','-') %最短路径虚线加粗

% y为菜市场每天需求，z为菜市场短缺1单位蔬菜的损失，p为收购点每天的收购量
y = [80, 70, 90, 80, 120, 70, 100, 90];
z = [10, 8, 5, 10, 10, 8, 5, 8];

prob = optimproblem;
% 要求解的变量多了一个p
x = optimvar('x',3,8, 'LowerBound',0);
p = optimvar('p',3,1, 'LowerBound',0);
obj = sum(sum(c.*x))+sum(z.*(y-sum(x)));
prob.Objective = obj;
% 约束条件
prob.Constraints.con1 = sum(sum(x))==sum(p);
prob.Constraints.con2 = sum(x) == y;
prob.Constraints.con3 = sum(x,2) == p;
prob.Constraints.con4 = sum(p) >= sum(y);
[sol, fval, flag, out] = solve(prob)
fval
% 输出x
sol.x
% 输出p
sol.p
writematrix(sol.x,'data2_1.xlsx','Sheet', 4)

求解

利用MATLAB软件对上述模型进行求解，从计算结果得知，求得问题三的总损失的最小值为10200元。最佳调运路线不变，具体的问题三的最佳供应方案如下表所示。

5结果分析

本次练习通过对江平市A、B、C三个蔬菜收购点向全市①到⑧八个菜市场的蔬菜供应方案的设计问题进行研究，使用Dijkstra算法计算各收购点至各菜市场之间的最短路径，根据题目信息建立线性规划模型，并对不同约束条件下的三个问题进行模型求解。对求解结果进行分析可知，最短路径算法与线性规划模型可以有效求解此类问题。文章来源地址https://www.toymoban.com/news/detail-536719.html

到了这里，关于图论＋线性规划建模——蔬菜供应方案的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！