968.监控二叉树
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。

输入:[0,0,null,0,0]
输出:1
解释:如图所示,一台摄像头足以监控所有节点。
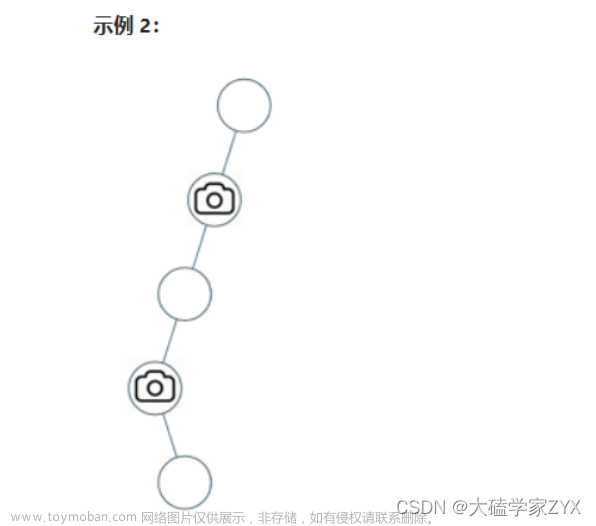
输入:[0,0,null,0,null,0,null,null,0]
输出:2
解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
- 给定树的节点数的范围是
[1, 1000]。 - 每个节点的值都是 0。
思路
本题一个重要思路是,二叉树中一定是叶子节点数量大于根节点数量的。叶子节点和根节点比起来,数量呈现指数级的扩大,因此我们想要用最少的摄像头,就要在叶子节点上优先想如何节约摄像头。
在叶子节点的情况下,我们要优先在叶子节点的父节点上放摄像头,然后一层一层往上推,往上推的逻辑是每隔2个节点放一个摄像头。
遍历顺序
因为我们从叶子节点开始,从下往上处理二叉树,所以一定是后序遍历。遍历的同时,我们需要记录每个节点的状态,从而根据左右孩子的状态去确定父节点的状态。
这里就涉及到一个状态转移的问题,但是本题的状态转移和动规的状态转移不同,本题只是涉及到一个每个节点状态的判断,并不是要得到最优状态。本题中节点有三种状态:
- 0:无摄像头,无覆盖
- 1:有摄像头
- 2:无摄像头,有覆盖(在摄像头范围内)
我们在后序遍历的时候,可以通过状态转移,来判断左右孩子是某状态的时候,父节点应该是什么状态。
空节点处理
本题的目的,就是尽可能让叶子节点的父节点去放摄像头,这样摄像头数目才能最少。为了让叶子节点的父节点能放摄像头,空节点应该是有覆盖的状态。
也就是说,遇到空节点应该向上返回2,这样才能让叶子节点父节点有摄像头。
情况列举
- 当前节点左右孩子都无摄像头有覆盖,也就是状态2,此时当前节点必然是状态0

- 当前节点左右孩子至少有一个无覆盖,此时当前节点一定要装一个摄像头,也就是状态1,否则就不能全覆盖了

- 左右孩子至少有一个有摄像头,那么当前节点一定是2

-
最后一种情况是基于第一种情况,第一种情况的当前节点无覆盖,需要等待父节点去把他覆盖。但是第一种情况的节点,如果是根节点,就没有父节点可以装摄像头!
此时根节点本身必须装一个摄像头,否则根节点就是无覆盖的状态。
本题所有可能的情况就限于这四种。主要是分析出来前三种,第四种是遍历到最后对根节点进行单独的判断。
最开始的写法
class Solution {
public:
//摄像头个数
int result=0;
//后序遍历,有返回值,返回当前节点状态
int travelsal(TreeNode* root){
//后序终止条件
if(root==nullptr) return 2;//空节点返回状态2
//左右中 后序遍历
int left = travelsal(root->left);
int right = travelsal(root->right);
//判断情况,第一种,左右都有cover无摄像头 左右都是状态2
if(left==2&&right==2){
return 0;//无cover 返回0让父节点加摄像头
}
//第二种,左右有一个是0
if(left==0||right==0){
result++;
return 1;
}
//第三种,左右有一个有摄像头
if(left==1||right==1){
return 2;
}
//逻辑不会走到这里,只是为了有返回值
return -1;
}
int minCameraCover(TreeNode* root) {
travelsal(root);
cout<<travelsal(root)<<endl;
//第四种,root无cover,但是没有父节点了
if(travelsal(root)==0){
result++;
}
return result;
}
};
debug测试:travelsal的输出多了1
存在逻辑问题,travelsal的输出多了1

但是实际上,后序遍历的逻辑是正确的,但是主函数写法出了问题
报错的主函数:
int minCameraCover(TreeNode* root) {
travelsal(root);
cout<<travelsal(root)<<endl;
//第四种,root无cover,但是没有父节点了
if(travelsal(root)==0)
//if(state==0)
result++;
return result;
}
注意这里的问题是,函数重写一次就会重复运行一次,上面这段主函数代码,相当于travelsal运行了三次
第一次是travelsal(root);,第二次是cout<<travelsal(root)<<endl;,第三次是if(travelsal(root)==0),函数只要出现就会运行一次,而result是一个全局变量,每次运行都会在之前运行的基础上+1.
因此,这里才会出现全局变量是3,但是函数实际逻辑正确的情况,就是因为函数写了三次所以运行了三遍。(这是一个很基础的逻辑问题,函数重新写一次就会运行一次,即使是在cout里面重写,也会运行第二遍,希望下次不要犯这种离谱错误了)
修改版
- 把主函数写法改掉就可以了
class Solution {
public:
//摄像头个数
int result=0;
//后序遍历,有返回值,返回当前节点状态
int travelsal(TreeNode* root){
//后序终止条件
if(root==nullptr) return 2;//空节点返回状态2
//左右中 后序遍历
int left = travelsal(root->left);
int right = travelsal(root->right);
//判断情况,第一种,左右都有cover无摄像头 左右都是状态2
if(left==2&&right==2){
return 0;//无cover 返回0让父节点加摄像头
}
//第二种,左右有一个是0
if(left==0||right==0){
result++;
return 1;
}
//第三种,左右有一个有摄像头
if(left==1||right==1){
return 2;
}
//逻辑不会走到这里,只是为了有返回值
return -1;
}
int minCameraCover(TreeNode* root) {
int state = travelsal(root);
cout<<state<<endl;
//第四种,root无cover,但是没有父节点了
//if(travelsal(root)==0)
if(state==0)
result++;
return result;
}
};
或者主函数可以写成
- 比较简洁的写法,return也可以直接返回表达式,不容易出错
int minCameraCover(TreeNode* root) {
int state = travelsal(root);
return result+=(state==0?1:0);
}
二叉树注意点
- 前后序的区别主要在处理节点的顺序,处理当前节点需要下面节点的状态就会用后序,但是所有遍历的终止条件都是遇到空节点返回(也就是触底了才会return),前序也是遇到空节点才开始return
- 最后return -1 是因为逻辑不会走到这里但是函数需要一个返回值,return什么都可以
时间复杂度
- 时间复杂度: O(n),需要遍历二叉树上的每个节点
- 空间复杂度: O(n),本题的空间复杂度在于递归的返回值return,输入的二叉树本身是不算空间复杂度的,但是每遍历到一个节点都会return 0/1/2状态值,也就是说每次递归的返回值都占了一个int的内存。所以空间复杂度是return的数值,一共n个数值所以是O(n)
总结
本题的难点首先是要想到贪心的思路,要想得到最少摄像头,就必须在叶子节点的父节点上面放摄像头。
然后就是遍历和状态推导,首先要想到二叉树每个节点,都可以归结为三种状态;
第二,要想到二叉树每个叶子节点的状态去推当前节点的状态,一共可以归纳为四种情况;然后通过遍历在二叉树上进行状态推导,后序遍历的同时接收下面叶子节点的状态,从而判断出当前的状态和需不需要放置摄像头。文章来源:https://www.toymoban.com/news/detail-539153.html
难点在于情况的分析,不要想复杂,所有的情况就是3+1种(最后一种是根节点单独考虑)文章来源地址https://www.toymoban.com/news/detail-539153.html
到了这里,关于DAY41:贪心算法(十)监控二叉树的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!





