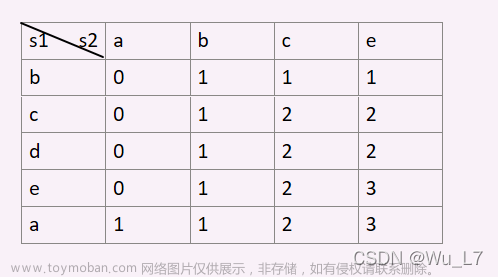
最长连续公共子序列
 文章来源:https://www.toymoban.com/news/detail-539217.html
文章来源:https://www.toymoban.com/news/detail-539217.html
题目链接:3692. 最长连续公共子序列 - AcWing题库文章来源地址https://www.toymoban.com/news/detail-539217.html
/*
解法:定义dp[i+1][j+1]为以a[i]结尾的字符串和b[j]结尾的字符串的最长连续公共子序列
那么对于a[i] == b[j]的时候 dp[i+1][j+1] == dp[i][j]+1否则为0 其他就是细枝末节
*/
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
const int N=1e2+11;
int dp[N][N];
int ans,ansi;
int main()
{
string a,b;
cin>>a>>b;
for(int i=0;i<a.size();i++){
for(int j=0;j<b.size();j++){
if(a[i]==b[j]){
dp[i+1][j+1] = dp[i][j]+1;
}
if(ans<=dp[i+1][j+1]){
ans = dp[i+1][j+1];
ansi = i;
}
}
}
cout<<ans<<endl;
for(int i =ans;i>0;i--){
cout<<a[ansi-i+1];
}
cout<<endl;
return 0;
}
#include<iostream>
#include<algorithm>
#include<string>
using namespace std;
const int N=1e2+11;
/*内存优化
滚动数组优化 对于dp[i][j]二维定义 每次dp[i+1][j+1]的计算只会引用dp[i][j]
那么0到i-1行的数据都是不使用的 故定义dp[i+1]在内层循环根据j的变化来代表
a[i]结尾的字符串和b[j]结尾的字符串的最长连续公共子序列
*/
int dp[N];
int ans,ansi;
int main()
{
string a,b;
cin>>a>>b;
for(int i=0;i<a.size();i++){
for(int j=b.size()-1;j>=0;j--){// 以dp[i+1][j+1]被压缩之前 只会引用dp[i][0~j]的数据 所以我们计算时候要从大往小算避免数据被提前错误跟新
if(a[i]==b[j]){
dp[j+1] = dp[j]+1;
}else dp[j+1]=0;
if(ans<=dp[j+1]){
ans = dp[j+1];
ansi = j;
}
}
}
cout<<ans<<endl;
for(int i =ans;i>0;i--){
cout<<b[ansi-i+1];
}
cout<<endl;
return 0;
}
到了这里,关于最长公共子序列LCA的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!