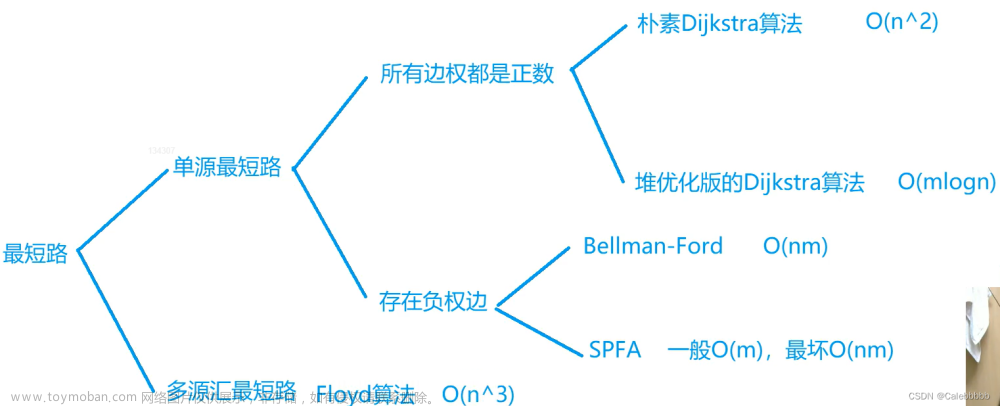
Bellman-Ford-贝尔曼-福特-算法求最短路-负环-Toy模板网

这篇具有很好参考价值的文章主要介绍了Bellman-Ford-贝尔曼-福特-算法求最短路-负环。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

Bellman-Ford算法（ O ( n m ) O(nm) O(nm)）

Bellman-Ford(贝尔曼-福特)算法基于松弛操作的单源最短路算法。

e[u]存u点的出边的邻点和边权，d[u]存u点到源点的距离。

初始化，ds]=0,d[其它点]=+o;
执行多轮循环。每轮循环，对所有边都尝试进行一次松弛操作；
当一轮循环中没有成功的松弛操作时，算法停止

为什么最坏需要n-1轮循环：n-1轮循环可以保证在有n个顶点的图中，从源节点到任意其他节点的最短路径都可以被找到。因为最长的简单路径最多包含n-1条边，所以进行n-1轮的松弛操作足以找到所有最短路径。

【模板】负环

题目描述

给定一个 $n$ 个点的有向图，请求出图中是否存在从顶点 $1$ 出发能到达的负环。

负环的定义是：一条边权之和为负数的回路。

输入格式

本题单测试点有多组测试数据。

输入的第一行是一个整数 $T$ ，表示测试数据的组数。对于每组数据的格式如下：

第一行有两个整数，分别表示图的点数 $n$ 和接下来给出边信息的条数 $m$ 。

接下来 $m$ 行，每行三个整数 $u, v, w$ 。

若 $\geq 0$ ，则表示存在一条从 $u$ 至 $v$ 边权为 $w$ 的边，还存在一条从 $v$ 至 $u$ 边权为 $w$ 的边。
若 $w < 0$ ，则只表示存在一条从 $u$ 至 $v$ 边权为 $w$ 的边。

输出格式

对于每组数据，输出一行一个字符串，若所求负环存在，则输出 YES，否则输出 NO。

样例 #1

样例输入 #1

样例输出 #1

NO
YES

提示

数据规模与约定

对于全部的测试点，保证：

$\leq n \leq 2 \times 10^3$ ， $\leq m \leq 3 \times 10^3$ 。
$\leq u, v \leq n$ ， $-10^4 \leq w \leq 10^4$ 。
$\leq T \leq 10$ 。

提示

请注意， $m$ 不是图的边数。

思路

利用Bellman-ford算法求负环即可，模版题文章来源地址https://www.toymoban.com/news/detail-539972.html

代码

#include <bits/stdc++.h>

#define int long long
using namespace std;
const int N = 2e3 + 10;
int n, m;

typedef struct node {
    int y, w;
} node;
vector<node> e[N];
int dist[N];


bool bellmanford() {
    for (int i = 1; i <= n; i++) dist[i] = 1e18;
    dist[1] = 0;
    bool flag;
    for (int i = 1; i <= n; i++) {
        flag = false;
        for (int j = 1; j <= n; j++) {
            if (dist[j] == 1e18) continue;
            for (auto [y, w]: e[j]) {
                if (dist[y] > dist[j] + w) {
                    dist[y] = dist[j] + w;
                    flag = true;
                }
            }
        }
        if (!flag) break;
    }
    return flag;
}

void solve() {
    cin >> n >> m;
    for (int i = 1; i <= n; i++) e[i].clear();
    for (int i = 1; i <= m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        e[a].push_back({b, c});
        if (c >= 0) e[b].push_back({a, c});
    }
    if (bellmanford()) {
        cout << "YES" << endl;
    } else {
        cout << "NO" << endl;
    }


}

signed main() {
#ifndef ONLINE_JUDGE
    freopen("test.in", "r", stdin);
    freopen("test.out", "w", stdout);
#endif
    int _;
    cin >> _;
    while (_--) solve();


    return 0;
}