算法 - 归并排序（Merge_sort）-Toy模板网

这篇具有很好参考价值的文章主要介绍了算法 - 归并排序（Merge_sort）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

什么是归并排序(Merging_sort)？

归并排序的适用场景：

演示归并排序的过程(默认arr和brr两个数组都是有序的)：

代码实现：

如果我们事先并没有分配好两个已经排序好的数组，而是直接的一个无序序列呢？

代码实现：

什么是归并排序(Merging_sort)？

在写归并排序的代码之前，我们先对归并排序的定义和排序原理进行梳理。

在严蔚敏的《数据结构（C语言版）》一书中对归并排序是这样定义的：

归并排序（Merging_Sort）是一类不同的排序方法。“归并”的含义是将两个或者两个以上的有序表组合成一个新的有序表。利用归并的思想容易实现排序，且这种实现方法已为读者熟悉，无论是顺序存储结构还是链表存储结构，都可以在O（m+n）的时间量级上实现。归并排序也是一个与插入排序、交换排序、选择排序不同的一类排序方法。

归并排序是一个基于分治法思想的算法，拿两个已经有序的序列重新组合成一个有序的序列。

归并排序的适用场景：

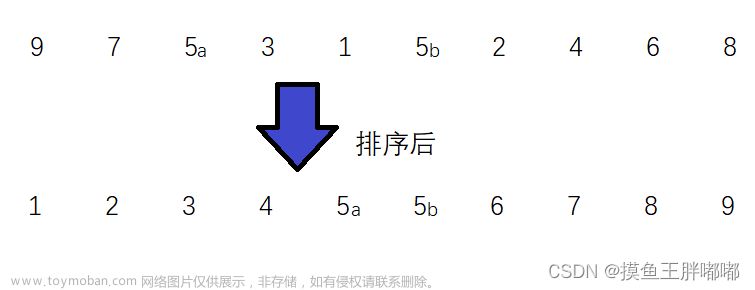
归并排序适合链表排序但不适合数组排序，归并在外部排序，比如磁盘文件的情况下比快速排序好，因为快排比较依赖数据的随机存取，而归并是顺序存取，对磁盘这种外村比较友好，还有很重要的一点就是快速排序和对排序都是不稳定排序，归并排序是稳定排序。

演示归并排序的过程(默认arr和brr两个数组都是有序的)：

例如我在这里给出两个数组：

int arr[] = {1,3,5,7};
int brr[] = {2,4,6,8};

我们定义两个指针i和j分别指向arr数组和brr数组，在定义一个临时值temp，通过遍历这两个数组，每一次的遍历我们都对i和j所指向的值进行比较，找到两个数中较小的值放入临时值temp中，并拷贝一份放入到新的数组中，直到排序完成：

归并排序,算法,数据结构,算法,c语言

当我们的i遍历至元素1，j遍历至元素2时，i是小于j的，于是我们将i所指向的元素赋值给temp并放入到新的数组中，令i指针向前迁移一位进行下一次i和j的比较：

归并排序,算法,数据结构,算法,c语言

此时继续i和j指向元素的比较，我们发现，元素2小于3，这时我们将元素2赋值给temp并放入新数组中，并令j指针的位置加1:

归并排序,算法,数据结构,算法,c语言

此时继续进行比较，我们发现3 < 4，现在将元素3赋值给temp，放入至新数组中，所对应i指针的位置向后迁移一位：

归并排序,算法,数据结构,算法,c语言

过程以此类推：

比较4和5: 归并排序,算法,数据结构,算法,c语言

比较5和6:

归并排序,算法,数据结构,算法,c语言

比较6和7:

归并排序,算法,数据结构,算法,c语言

比较7和8:

归并排序,算法,数据结构,算法,c语言

最后我们直接将元素8放至新数组的末尾：

归并排序,算法,数据结构,算法,c语言

同样的，如果我们的第二个数组的后面又加上9和10，我们在第一个数组已经遍历完了的情况下，直接将9和10安插在新数组的后面。

代码实现：

#include<stdio.h>
#include<assert.h>
#include<iostream>
void showar(int *ar,int len)
{
	assert(ar != nullptr);
	for(int i = 0;i < len;i++){
		printf("%d ",ar[i]);
	}
	printf("\n--------------------------\n");
}
void Merging_sort1(int *ar,int len1,int *br,int len2,int *temp)
{
	assert(ar != nullptr && br != nullptr && temp != nullptr);
	assert(len1 >= 0 && len2 >= 0);
	int i = 0,j = 0,k = 0;
	while(i < len1 && j < len2){
		if(ar[i] < br[j]){
			temp[k] = ar[i];
			i++;
			k++;
		}
		else{
			temp[k] = br[j];
			j++;
			k++;
		}
	}
	while(i < len1){
		temp[k] = ar[i];
		i++;
		k++;
	}
	while(j < len2){
		temp[k] = br[j];
		j++;
		k++;
	}
}
int main()
{
    int ar[4] = {1,3,5,7};
	int br[4] = {2,4,6,8};
	int len1 = sizeof(ar) / sizeof(ar[0]);
	int len2 = sizeof(br) / sizeof(br[0]);
	int temp[8] = {0};
	Merging_sort1(ar,len1,br,len2,temp);
	showar(temp,8);
	return 0;
}

我们对排序的代码做一下简洁优化（三目运算符）：

void Merging_sort1(int *ar,int len1,int *br,int len2,int *temp)
{
	assert(ar != nullptr && br != nullptr && temp != nullptr);
	assert(len1 >= 0 && len2 >= 0);
	int i = 0,j = 0,k = 0;
	while(i < len1 && j < len2){
		temp[k++] = ar[i] < br[j] ? ar[i++] : br[j++];
	}
	while(i < len1){
		temp[k++] = ar[i++];
	}
	while(j < len2){
		temp[k++] = br[j++];
	}
}

运行结果：

归并排序,算法,数据结构,算法,c语言

如果我们事先并没有分配好两个已经排序好的数组，而是直接的一个无序序列呢？

例如在这里我给出一个无序数组：

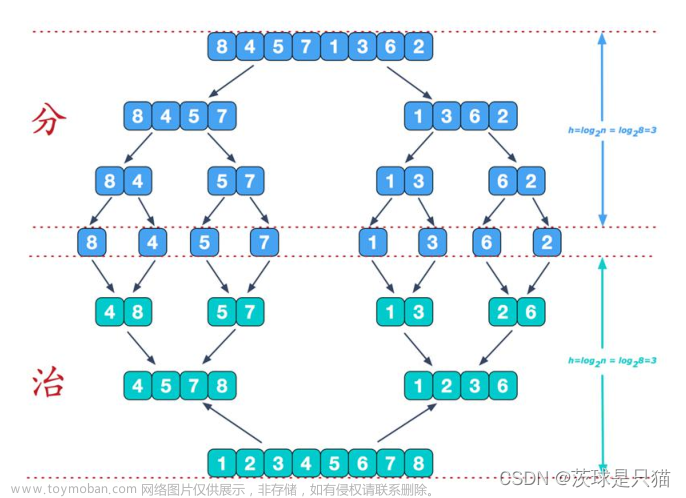
int arr[9] = {5,8,2,3,1,4,7,6};

归并排序的思想就是分治法，我们将数组中的8个数全部分成单一的数，把他们均看作是一个小数组：

归并排序,算法,数据结构,算法,c语言

现在形成了8个长度为1的数组，然后我们两两进行归并，并把相对较小的元素放在前面：

归并排序,算法,数据结构,算法,c语言

现在形成了4个长度为2的数组，我们继续进行两两归并：

这次我们对58和23进行归并，我们先放2再放3，然后依次放5和8，后面两个数组也是这样：

归并排序,算法,数据结构,算法,c语言

现在形成了两个长度为4的数组，继续对这两个数组进行归并：

归并排序,算法,数据结构,算法,c语言

代码实现：

#define MAXSIZE 11
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<iostream>
#include<time.h>
void initar(int *ar,int len)//初始化ar数组，用小于30的int类型数填充
{
	assert(ar != nullptr);
	for(int i = 0;i < len;i++){
		ar[i] = rand() % 30;
	}
}
void showar(int *ar,int len)//打印数组函数
{
	assert(ar != nullptr);
	for(int i = 0;i < len;i++){
		printf("%d ",ar[i]);
	}
	printf("\n--------------------------\n");
}
void merge(int *ar,int low,int middle,int high,int *temp)//归并排序
{
	int i = low;//通过I遍历左半边数组
	int j = middle + 1;//通过j遍历右半边数组
	int k = low;//通过k遍历整个数组
	while(i <= middle && j <= high){//循环通过I和j分别遍历从中间划分开来的两个数组，并分开比较大小
		temp[k++] = ar[i] < ar[j] ? ar[i++] : ar[j++];//如果前者小于后者就将前者直接添加至新数组的后面，依此类推
	}
	while(i <= middle)//如果比较完了，但左半边数组还有剩余的元素，直接将这些元素添加至新数组的后方
	temp[k++] = ar[i++];
	while(j <= high)//同理，比较完了右半边还有剩余的，也直接添加至新数组的后方
	temp[k++] = ar[j++];
	for(i = low;i <= high;i++){//最后将新数组的所有元素赋值给ar数组
		ar[i] = temp[i];
	}
}
void merge_sort(int *ar,int low,int high,int *temp)
{
	if(low >= high){//如果左边界大于右边界，直接返回
		return;
	}
	int middle = low + (high - low) / 2;//相比较（low + high）/ 2；的优化写法，可以防止越界
	merge_sort(ar,low,middle,temp);递归调用，左半部分循环归并
	merge_sort(ar,middle + 1,high,temp);//右半部分循环归并
	merge(ar,low,middle,high,temp);//递归操作
}
void mergesort(int *ar,int len)//最终归并函数
{
	int *temp = (int *)malloc(sizeof(int)*len);//向堆区申请len个int类型大小的空间赋给temp新数组
	assert(temp != nullptr);//断言新数组不为空
	merge_sort(ar,0,len - 1,temp);//递归归并操作
	free(temp);//释放temp的内存空间
    temp = NULL;//将temp置空
}
int main()
{
    srand((unsigned int)time(NULL));
	int ar[MAXSIZE];
	initar(ar,MAXSIZE);
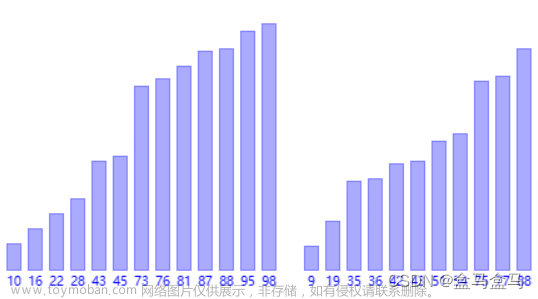
	printf("原始数据为：\n");
	showar(ar,MAXSIZE);
    printf("\n经过归并排序后的数据为：\n");
	mergesort(ar,MAXSIZE);
	showar(ar,MAXSIZE);
	return 0;
}

运行结果：

归并排序,算法,数据结构,算法,c语言