图的拓扑排序-Toy模板网

这篇具有很好参考价值的文章主要介绍了图的拓扑排序。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

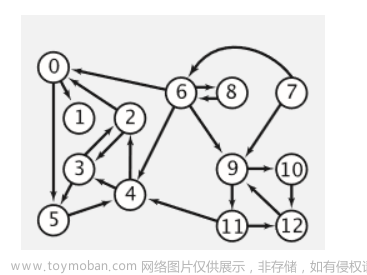
拓扑排序是一个有向无环图（有向图、弧不形成闭环）的所有顶点的线性序列。该线性序列中，图的每个顶点只出现一次，若顶点A到顶点B之间存在有向弧<v1,v2>,则顶点A一定在顶点B前面。

图的拓扑排序,图,数据结构,图论

图的拓扑排序实现很简单，基本操作思想：

1、开始时用一个辅助数组记录各顶点的入度，入度为0的顶点全部入队（先进先出、输入顶点）

2、将入度为0的顶点逐个出队，出队时，将以他们为弧尾的弧的弧头的入度-1，若入度为0，则将弧头入队。重复入队、出队，直到所有顶点出队完。

图的拓扑排序,图,数据结构,图论

图中只有顶点A的入度为0，将顶点A入队；将A出队，同时减少以顶点A为弧尾的弧的弧头（图中为顶点2、顶点4）的入度。发现顶点2的入度为0，将顶点2入队。如此重复入队、出队，直到所有顶点输出完。

图的拓扑排序,图,数据结构,图论

最终的到拓扑排序结果：1、2、4、3、5（不唯一）文章来源地址https://www.toymoban.com/news/detail-540370.html

// 无回路的有向图
// 拓扑排序
void TopologicaSort(ALGraph &graph) {
	int Degree[MAX_VERTEX_NUM];	// 记录各顶点当前的入度
	for (int i = 0; i < graph.ver_num; ++i) {
		Degree[i] = 0;
	}
	for (int i = 0; i < graph.ver_num; ++i) {
		ArcNode* T = graph.adj[i].first;
		while (T) {
			++Degree[T->adjIndex];	// 邻接顶点入度+1
			T = T->Next;
		}
	}
	queue<verType> VERTEX;
	for (int i = 0; i < graph.ver_num; ++i) {
		if (0 == Degree[i]) {
			VERTEX.push(graph.adj[i].vertex);	// 入度为0的顶点入队
			break;
		}
	}
	verType vex;
	int index;
	while (!VERTEX.empty()) {
		vex = VERTEX.front();
		VERTEX.pop();
		cout << vex << " ";
		index = LocateVertex(graph, vex);
		if (index < 0) break;
		ArcNode* T = graph.adj[index].first;
		while (T) {
			--Degree[T->adjIndex];
			if (0 == Degree[T->adjIndex]) VERTEX.push(graph.adj[T->adjIndex].vertex);
			T = T->Next;
		}
	}
	cout << endl;
}

到了这里，关于图的拓扑排序的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！