正态分布的分布函数和概率密度（matplotlib）-Toy模板网

这篇具有很好参考价值的文章主要介绍了正态分布的分布函数和概率密度（matplotlib）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

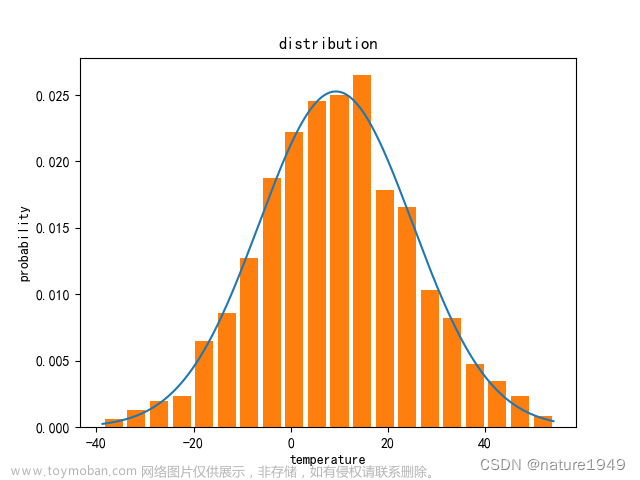
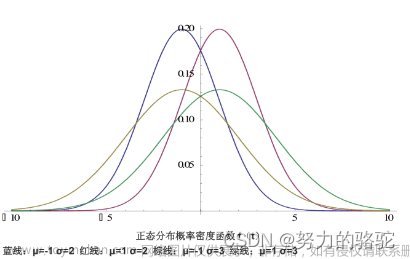
绘制正态分布的分布函数和概率密度曲线

1.正态分布的概率密度函数和分布函数：

正态分布概率密度,概率论,数据可视化,python

2.代码实现：

import sympy
import numpy as np
import matplotlib.pyplot as plt


# -----------构造数据--------------
# u=0 σ=1
x_1, m_1 = [], []
y_1, n_1 = [], []
for i in np.arange(-10, 10, 0.1):
    x_1.append(i)
    y_1.append(np.exp(-(i * i / 2.0))/np.sqrt(2*np.pi))

    x = sympy.symbols('x')
    y = sympy.exp(-(x * x / 2.0))/sympy.sqrt(2*np.pi)
    Y = sympy.integrate(y)
    res = Y.subs(x, i) - Y.subs(x, -float('inf'))
    m_1.append(i)
    n_1.append(res)
# u=0 σ=2
x_2, m_2 = [], []
y_2, n_2 = [], []
for i in np.arange(-10, 10, 0.1):
    x_2.append(i)
    y_2.append(np.exp(-(i * i / (2.0*2*2)))/(np.sqrt(2*np.pi)*2))

    x = sympy.symbols('x')
    y = sympy.exp(-(x * x / (2.0*2*2))) / (sympy.sqrt(2 * np.pi)*2)
    Y = sympy.integrate(y)
    res = Y.subs(x, i) - Y.subs(x, -float('inf'))
    m_2.append(i)
    n_2.append(res)
# u=1 σ=1
x_3, m_3 = [], []
y_3, n_3 = [], []
for i in np.arange(-10, 10, 0.1):
    x_3.append(i)
    y_3.append(np.exp(-((i-1) ** 2 / 2.0)) / np.sqrt(2 * np.pi))

    x = sympy.symbols('x')
    y = sympy.exp(-((x-1) ** 2 / 2.0)) / sympy.sqrt(2 * np.pi)
    Y = sympy.integrate(y)
    res = Y.subs(x, i) - Y.subs(x, -float('inf'))
    m_3.append(i)
    n_3.append(res)

# --------------可视化概率密度函数---------------------------
plt.title("正态分布概率密度")                       # 设置标题
plt.rcParams['font.sans-serif'] = 'KaiTi'        # 设置字体
plt.rcParams['axes.unicode_minus'] = False       # 正常显示负号
plt.plot(x_1, y_1, c='red', label='μ=0 σ=1')     # 添加数据
plt.plot(x_2, y_2, c='green', label='μ=0 σ=2')   # 添加数据
plt.plot(x_3, y_3, c='blue', label='μ=1 σ=1')    # 添加数据
plt.xlabel('x', loc='right')                     # x轴标签
plt.ylabel('y', loc='top')                       # y轴标签
plt.legend(framealpha=1, frameon=True)           # 添加图标
plt.show()                                       # 展示

# --------------可视化分布函数---------------------------------
plt.title("正态分布分布函数")
plt.rcParams['font.sans-serif'] = 'KaiTi'
plt.rcParams['axes.unicode_minus'] = False
plt.plot(m_1, n_1, c='red', label='μ=0 σ=1')
plt.plot(m_2, n_2, c='green', label='μ=0 σ=2')
plt.plot(m_3, n_3, c='blue', label='μ=1 σ=1')
plt.xlabel('x', loc='right')
plt.ylabel('y', loc='top')
plt.legend(framealpha=1, frameon=True)
plt.show()