分支限界法求0-1背包问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了分支限界法求0-1背包问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

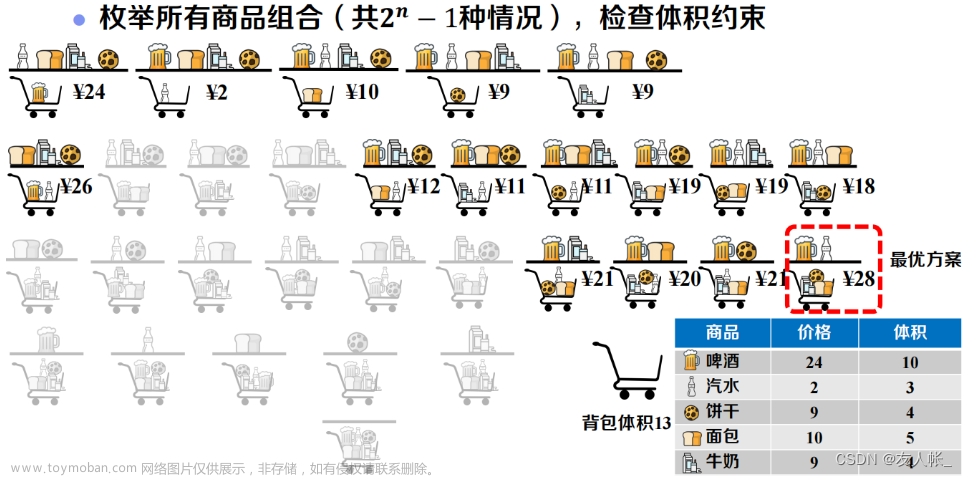
使用分支限界法求解01背包问题，3个物品，重量和价值，背包容量

（1）画出解空间树

（2）Say如何剪枝

（3）求出最优解

假设物品的个数n=3，背包容量W = 30，重量w =（16,15,15），价值v =（45,25,25）

（1）队列式(FIFO)分支限界法：按照队列先进先出（FIFO）原则选取下一个结点为扩展结点。
（2）优先队列式分支限界法：按照优先队列中规定的优先级选取优先级最高的结点成为当前扩展结点。

（1）画出解空间树

迷惑点：解空间树书上给的是一个排列树，把超重的情况也画出来了，其实是无用功，那么如果考虑超重的话，就在D的时候就已经超重了，就不需要画出来，但是书上却把它称之为搜索空间树，所以我们画解空间树应该画哪种呢？

a.队列分支限界法

01背包分支限界法,算法,算法

b.优先队列分支限界法：当前价值高的节点优先

01背包分支限界法,算法,算法

（2）Say如何剪枝

限界函数代码：

void bound(NodeType &e)   //计算分支结点e的上界
{ 
int i=e.i+1;
int sumw=e.w;
double sumv=e.v;
while((sumw+w[i]<=W)&&i<=n)
{
  sumw+=w[i];
  sumv+=v[i];
  i++;
}
if(i<=n)               //余下物品只能部分装入
   e.ub=sumv+(W-sumw)*v[i]/w[i];
else                   //余下物品全部可以装入
   e.ub=sumv; 
}

剪枝：如果超重需要剪枝，如果这个结点对应的上界不比当前最优值更大，则说明相应的子树不含问题的最优解，因此该节点也需要剪枝。

（3）求出最优解

01背包分支限界法,算法,算法