这篇具有很好参考价值的文章主要介绍了R——投入产出表，直接消耗系数矩阵，完全消耗系数矩阵。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。
library(aTSA)
Q=read.csv("D:Q2017.csv")
X=read.csv("D:X2017.csv")
#直接消耗系数A
Q1<-as.matrix(Q)
X_1<-diag(1/X$total)
A<-Q1%*%X_1
#完全消耗系数B
I<-diag(length(X$total))
B<-solve(I-A)-I
write.csv(B,file="D:B2017.csv")数据原始
文章来源地址https://www.toymoban.com/news/detail-543348.html
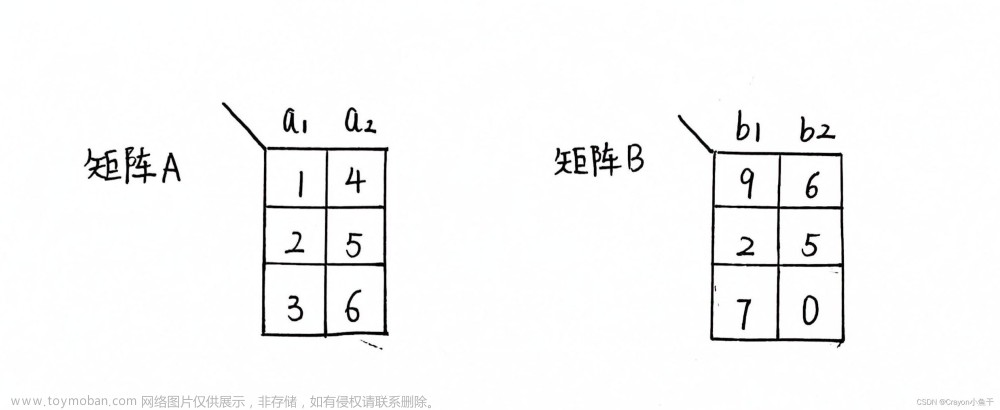
Q2017中间投入表
X2017总投入
文章来源：https://www.toymoban.com/news/detail-543348.html
到了这里，关于R——投入产出表，直接消耗系数矩阵，完全消耗系数矩阵的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！
计算相关系数矩阵，原始数据如下： 计算相关系数矩阵代码如下： 计算结果保存到工作表，打开结果如下：
现要求解系数矩阵由16 阶Hilbert 方程组构成的线性方程组，右端项为 即要求解方程组Ax = b，其中 A=A0,b=b0 分别用高斯-赛德尔方法、最速下降法、共轭梯度法求解如下。 2.1. 高斯-赛德尔方法 2.2. 最速下降法 2.3. 共轭梯度法 在最速下降法中，搜索方向p取的是函数减
创作日志： Pearson或Spearson代表的是两个变量之间的相关性，因此一般输入是两个向量(vector)，那么当我们有多个变量时，怎样计算他们两两之间的相关性系数呢？得到的correlation matrix各元素代表的又是什么意思呢？ 举例： 矩阵A有两个样本：a1 与 a2，矩阵B有两个样本：b1 与
齐次方程组： A x = 0 Ax=0 A x = 0 系数矩阵 A n × n A_{n×n} A n × n 的秩 解的个数 满秩： r ( A ) = n r(A)=n r ( A ) = n 仅有零解 不满秩： r ( A ) = r n r(A)=rn r ( A ) = r n 有无穷多解 注： 齐次线性方程 A x = 0 Ax=0 A x = 0 一定有解. 当 r ( A ) = r n r(A)=rn r ( A ) = r n 时， 基础解系 （线性无关的
对于一个随机变量的分布特征，可以由均值、方差、标准差等进行描述。而对于两个随机变量的情况，有协方差和相关系数来描述两个随机变量的相互关系。 本文主要参考概率论与数理统计的教科书，整理了协方差、样本协方差、协方差矩阵、相关系数的概念解释和代码。
用户精度 (User’s Accuracy): 假设分类结果的某类别的用户精度为 80%，则用户拿到分类结果后，10个像元中有8个是对的，2个是错的； 生产者精度 (Producer’s Accuracy): 假设分类结果的某类别的生产者精度为 80%，那么如果该类别有10个像素的话，则有2个没有分到该类别（丢失了）。
标量（scalar） ：一个单独的数。 向量（vector） ：⼀组有序排列的数。通过次序中的索引，我们可以确定每个单独的数。 矩阵（matrix） ：具有相同特征和纬度的对象的集合。⼀个对象表⽰为矩阵中的⼀⾏，⼀个特征表⽰为矩阵中的⼀列，表现为⼀张⼆维数据表。 张量（ten
给多光谱遥感图像各个波段绘制热力图，首先需要计算波段之间的相关系数矩阵，而计算遥感图像波段相关系数矩阵有不同的方法，常用的我们可以采用遥感图像处理软件计算，比如ENVI软件就可以计算相关系数矩阵，使用工具箱中的Statistics工具即可进行多种统计运算。 我们
类型 符号 LaTeX 二项式系数 ( n k ) binom{n}{k} ( k n ) binom{n}{k} 小型二项式系数 ( n k ) tbinom{n}{k} ( k n ) tbinom{n}{k} 大型二项式系数 ( n k ) dbinom{n}{k} ( k n ) dbinom{n}{k} x y z v begin{matrix}x y \\\\z vend{matrix} x z y v ∣ x y z v ∣ begin{vmatrix}x y \\\\z vend{vmatrix} x z y v ∥
邻接矩阵：很简单，就是两个点有关系就是1，没有关系就是0 可达性矩阵：非常简单，两点之间有路为1，没有路为0 可发行矩阵的计算 ：有n个元素，初始可达性矩阵为A，那么最终的矩阵 B= 完全关联矩阵：描述点与边的关系，如果该点和该边有关系为1，没有关系就为0，非常
