回归预测 | MATLAB实现WOA-DNN鲸鱼算法优化深度神经网络的数据多输入单输出回归预测
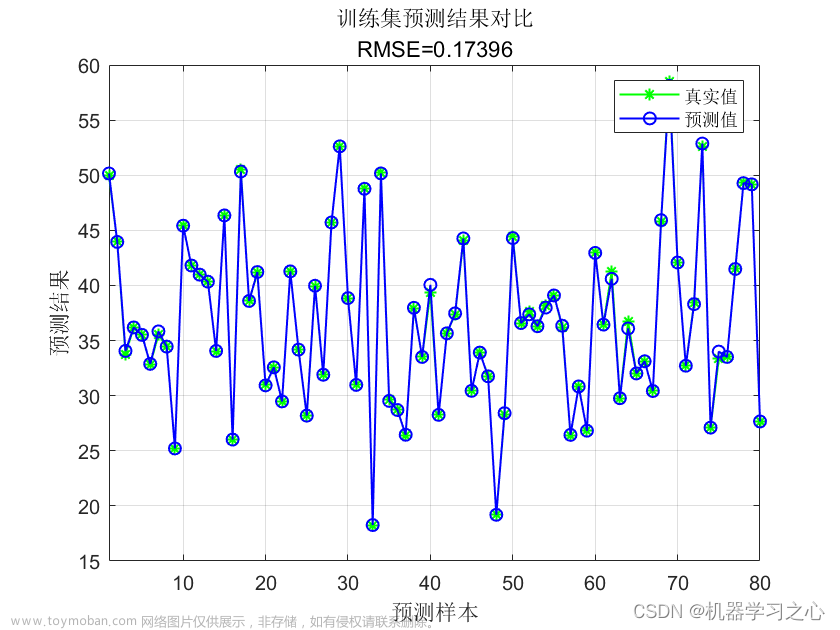
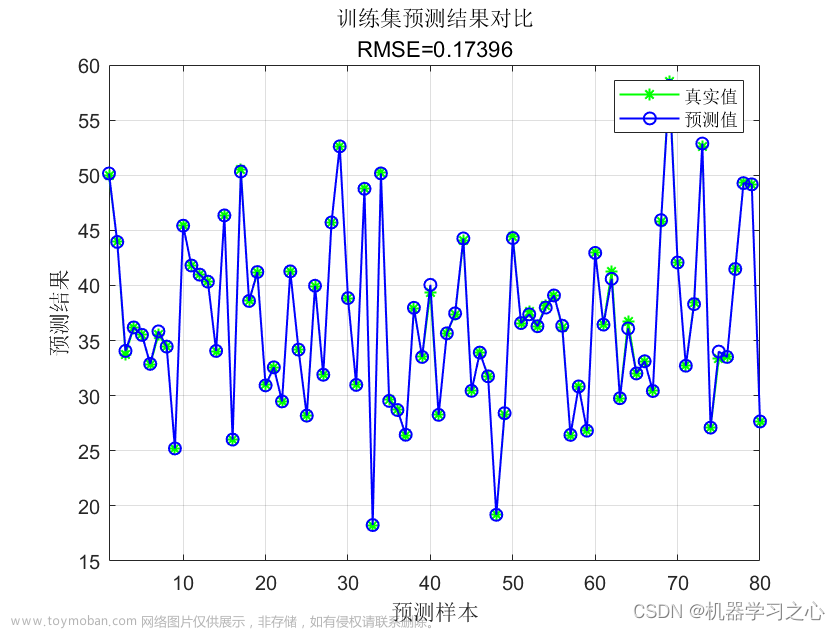
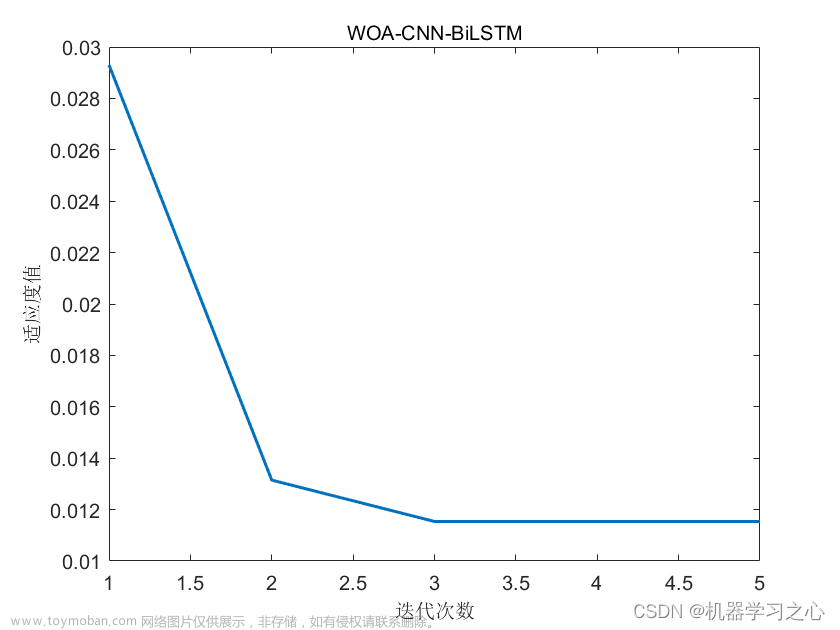
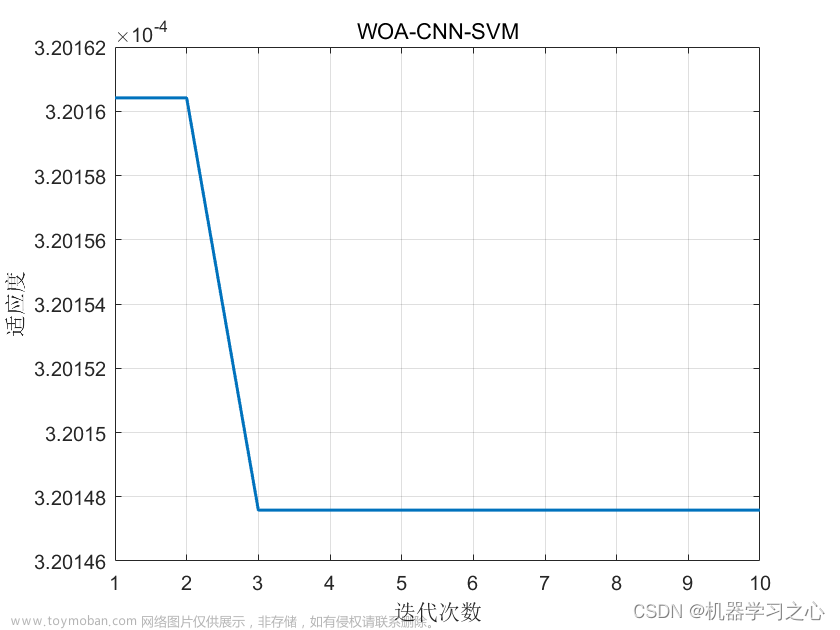
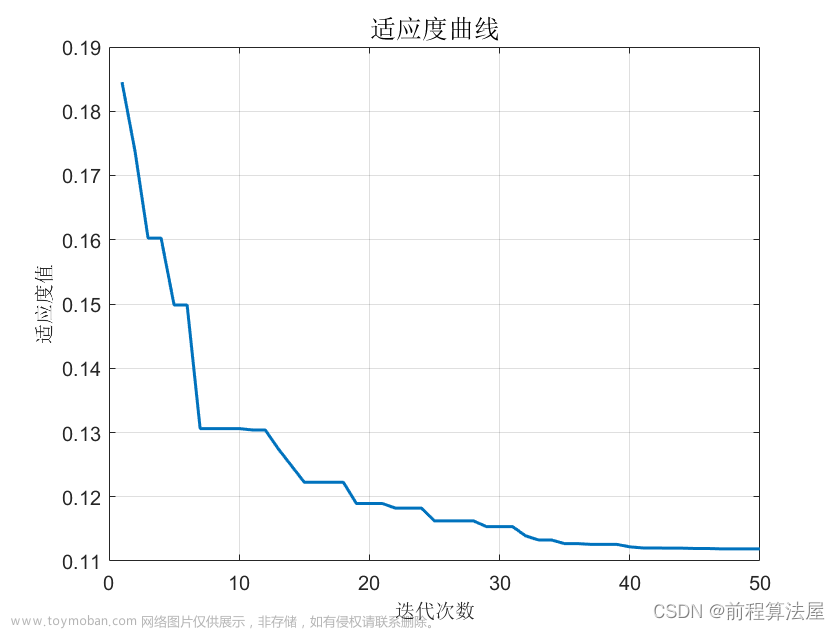
效果一览






基本介绍
回归预测 | MATLAB实现WOA-DNN鲸鱼算法优化深度神经网络的数据多输入单输出回归预测
MATLAB实现WOA-DNN鲸鱼算法优化深度神经网络的数据多输入单输出回归预测(Matlab完整程序和数据)
输入7个特征,输出1个,即多输入单输出;优化参数为学习率,批大小,正则化系数。
运行环境Matlab2018及以上,运行主程序main即可,其余为函数文件无需运行,所有程序放在一个文件夹,data为数据集;
命令窗口输出RMSE、MAE、R2、MAPE。文章来源:https://www.toymoban.com/news/detail-543721.html
程序设计
- 完整程序和数据下载方式1(订阅《DNN深度神经网络》专栏,同时可阅读《DNN深度神经网络》专栏收录的所有内容,数据订阅后私信我获取):MATLAB实现WOA-DNN鲸鱼算法优化深度神经网络的数据多输入单输出回归预测
- 完整程序和数据下载方式2(订阅《智能学习》专栏,同时获取《智能学习》专栏收录程序3份,数据订阅后私信我获取):MATLAB实现WOA-DNN鲸鱼算法优化深度神经网络的数据多输入单输出回归预测
%% 记录最佳参数
Best_pos(1, 2) = round(Best_pos(1, 2));
best_lr = Best_pos(1, 1);
best_hd = Best_pos(1, 2);
best_l2 = Best_pos(1, 3);
%% 建立模型
% ---------------------- 修改模型结构时需对应修改fical.m中的模型结构 --------------------------
layers = [
sequenceInputLayer(f_) % 输入层
fullyConnectedLayer(outdim) % 输出回归层
regressionLayer];
%% 参数设置
% ---------------------- 修改模型参数时需对应修改fical.m中的模型参数 --------------------------
options = trainingOptions('adam', ... % Adam 梯度下降算法
'MaxEpochs', 500, ... % 最大训练次数 500
'InitialLearnRate', best_lr, ... % 初始学习率 best_lr
'LearnRateSchedule', 'piecewise', ... % 学习率下降
'LearnRateDropFactor', 0.5, ... % 学习率下降因子 0.1
'LearnRateDropPeriod', 400, ... % 经过 400 次训练后 学习率为 best_lr * 0.5
'Shuffle', 'every-epoch', ... % 每次训练打乱数据集
'ValidationPatience', Inf, ... % 关闭验证
'L2Regularization', best_l2, ... % 正则化参数
'Plots', 'training-progress', ... % 画出曲线
'Verbose', false);
%% 训练模型
net = trainNetwork(p_train, t_train, layers, options);
%% 仿真验证
t_sim1 = predict(net, p_train);
t_sim2 = predict(net, p_test );
%% 数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);
T_sim1=double(T_sim1);
T_sim2=double(T_sim2);
%% 均方根误差
error1 = sqrt(sum((T_sim1 - T_train).^2) ./ M);
error2 = sqrt(sum((T_sim2 - T_test ).^2) ./ N);
%_________________________________________________________________________%
% The Whale Optimization Algorithm
function [Best_Cost,Best_pos,curve]=WOA(pop,Max_iter,lb,ub,dim,fobj)
% initialize position vector and score for the leader
Best_pos=zeros(1,dim);
Best_Cost=inf; %change this to -inf for maximization problems
%Initialize the positions of search agents
Positions=initialization(pop,dim,ub,lb);
curve=zeros(1,Max_iter);
t=0;% Loop counter
% Main loop
while t<Max_iter
for i=1:size(Positions,1)
% Return back the search agents that go beyond the boundaries of the search space
Flag4ub=Positions(i,:)>ub;
Flag4lb=Positions(i,:)<lb;
Positions(i,:)=(Positions(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
% Calculate objective function for each search agent
fitness=fobj(Positions(i,:));
% Update the leader
if fitness<Best_Cost % Change this to > for maximization problem
Best_Cost=fitness; % Update alpha
Best_pos=Positions(i,:);
end
end
a=2-t*((2)/Max_iter); % a decreases linearly fron 2 to 0 in Eq. (2.3)
% a2 linearly dicreases from -1 to -2 to calculate t in Eq. (3.12)
a2=-1+t*((-1)/Max_iter);
% Update the Position of search agents
for i=1:size(Positions,1)
r1=rand(); % r1 is a random number in [0,1]
r2=rand(); % r2 is a random number in [0,1]
A=2*a*r1-a; % Eq. (2.3) in the paper
C=2*r2; % Eq. (2.4) in the paper
b=1; % parameters in Eq. (2.5)
l=(a2-1)*rand+1; % parameters in Eq. (2.5)
p = rand(); % p in Eq. (2.6)
for j=1:size(Positions,2)
if p<0.5
if abs(A)>=1
rand_leader_index = floor(pop*rand()+1);
X_rand = Positions(rand_leader_index, :);
D_X_rand=abs(C*X_rand(j)-Positions(i,j)); % Eq. (2.7)
Positions(i,j)=X_rand(j)-A*D_X_rand; % Eq. (2.8)
elseif abs(A)<1
D_Leader=abs(C*Best_pos(j)-Positions(i,j)); % Eq. (2.1)
Positions(i,j)=Best_pos(j)-A*D_Leader; % Eq. (2.2)
end
elseif p>=0.5
distance2Leader=abs(Best_pos(j)-Positions(i,j));
% Eq. (2.5)
Positions(i,j)=distance2Leader*exp(b.*l).*cos(l.*2*pi)+Best_pos(j);
end
end
end
t=t+1;
curve(t)=Best_Cost;
[t Best_Cost]
end
参考资料
[1] https://blog.csdn.net/kjm13182345320/article/details/129215161
[2] https://blog.csdn.net/kjm13182345320/article/details/128105718文章来源地址https://www.toymoban.com/news/detail-543721.html
到了这里,关于回归预测 | MATLAB实现WOA-DNN鲸鱼算法优化深度神经网络的数据多输入单输出回归预测的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!