数学建模中所需要使用到的Matlab（从零开始介绍）

注意事项：只有将Matlab的工作目录切换到当前文件夹中，才能运行当前程序。文章来源地址https://www.toymoban.com/news/detail-543783.html

%% 第一节课 层次分析法（AHP）

% 1.分号的使用：每一行的语句最后可以选择性地加上分号，加上分号后不显示运行结果(因此大部分语句加上分号），否则显示运行结果
   a=3;
   b=5
   
% 2.注释的使用：用百分号表示注释，多行注释快捷键为Ctrl+R，取消注释的快捷键为Ctrl+T
% 用连续的两个百分号表示加粗的注释部分

% 3.clear和clc：clear可以清空工作区内的变量，clc可以实现命令行窗口清屏，常连用clear;clc来进行脚本初始化，防止原先内容的干扰
   clear;clc
   
% 4.输入输出函数：
% ①输出函数disp()：类似于C语言中的printf()函数，内部参数可以是一个变量或者常量
%   disp函数可以不用加上分号，因为结果一定会显示出来
% ②输入函数input()：类似于Python中的input函数，参数为输入提示信息
  A=input("请输入A的值：")
  
% 5.向量的表示：
% ①行向量用[]表示，各个元素之间用逗号或者空格来分隔
   a=[1 2 3];a=[1,2,3]
% ②列向量的表示类似，用分号分隔每一行的元素
   a=[1;2;3]
   
% 6.字符串类型：
% ①字符串常量可以用一对单引号或者双引号来表示
% ②字符串合并的两种方法：首先可以使用strcat(str1,str2...)函数，也可以使用[str1,str2...]或者[str1 str2...]的形式
  str=strcat("字符串1","字符串2"); str=['字符串1','字符串2']
% ③num2str()函数：将数字类型转化为字符串
  c=100;num2str(c)
  
% 7.矩阵类型：
% ①表示方法：仍然用[]表示，同行元素之间用逗号或者空格隔开，用分号来分隔列
    E=[1 2;3 4;5 6]
% ②矩阵中指定位置的元素（第m行第n列）：使用 矩阵名（行数，列数） 即可
    E=[1 2;3 4;5 6];E(2,1)
% ③矩阵中某一行或某一列的全部元素：使用矩阵名（行数，：）/ 矩阵名（：，列数），分别得到一个行向量和列向量
    E=[1 2;3 4;5 6];E(2,:)
% ④矩阵中某些行或某些列的全部元素：使用矩阵名（[行1，行2..],:）的形式，输出为一个矩阵
    E=[1 2;3 4;5 6];E([2,3],:)
% ⑤矩阵中的全部元素：使用矩阵名（：）即可，将矩阵中的所有元素逐列排成一个列向量返回
    E=[1 2;3 4;5 6];E(:)
% ⑥可以用end表示矩阵的最后一行的行数

% 8.求和函数sum():(求积函数prod同理，只是运算由加法变成了乘法）
% ①当参数为向量时，无论是行向量还是列向量，都是直接求和
    E=[1 2 3];sum(E)
    E=[1;2;3];sum(E)
% ②当参数为矩阵时，第二个参数为1（默认情况）时为按列求和得到一个行向量，第二个参数为2时为按行求和得到一个列向量
    E=[1 2;3 4;5 6];a=sum(E,1)
    E=[1 2;3 4;5 6];a=sum(E,2)
% ③对整个矩阵进行求和时，可以连续两次调用sum函数

% 9.等差数列的表示方法：生成从a到b（闭区间），公差为d（默认为1，也可以为负数）的一组等差数列的方法：a:d:b
    1:10:100
    
% 10.size函数：语法为size（矩阵名），返回一个两个元素的行向量，分别表示矩阵的行数和列数
    E=[1 2;3 4;5 6];size(E)
%    只需要返回行数可以使用size(矩阵名，1），只需要返回列数可以使用size（矩阵名，2）

% 11.矩阵重复函数repmat():语法为：repmat（矩阵名，行数，列数）作用：将原矩阵视为新矩阵的一个元素，构造指定行数和列数的新矩阵
    E=[1 2;3 4;5 6];repmat(E,2,2)
    
% 12.矩阵的运算：
% ①矩阵的加减法：直接使用‘+’‘-’号即可
    E1=[1 2;3 4;5 6];E2=[1 1;1 1;1 1]
    Temp=E1+E2
% ②矩阵的乘除法：直接使用‘*’‘/’号即可
    E1=[1 2;3 4;5 6];E2=[1 1 1;1 1 1];E3=[1 1;1 1;1 1]
    Temp1=E1*E2
    Temp2=E1/E3
% ③矩阵的逆矩阵：inv（矩阵名）注意：只有方阵才有逆矩阵
     E=[1 2;3 4];E*inv(E)
% ④两个形状完全相同的矩阵的对应元素的乘除法：使用‘.*’和‘.\’即可实现
     E1=[1 1;1 1];E2=[2 2;2 2];E1./E2
% ⑤矩阵与常数相乘(或者相除），使用直接乘法（除法）或者点乘（点除）都可以
     E=[1 1;1 1];E*2
% ⑥矩阵的乘方使用'^'号即可，如果需要每个元素求乘方，则需要使用'.^'
     E=[2 2;2 2];E^3
     
% 13.求矩阵的特征值和特征向量：使用 eig（矩阵名）即可
% ①只计算特征值：用一个变量接收结果，返回矩阵特征值构成的列向量
     E=[1 2;3 4];A=eig(E)
% ②计算特征值和特征向量：用两个变量接收结果，第一个变量得到由特征列向量排列得到的矩阵，第二个变量得到对角阵，对角阵上的元素为特征值
     E=[1 2;3 4];[A,B]=eig(E)
     
% 14.find函数找出非零元素的位置：
% ①对向量使用时，可以找出前k个(默认为所有元素）不为零的元素的位置：find（向量名,k），返回一个行向量
     E=[0 1 0 2 0 3];find(E,3)
% ②对矩阵直接使用时，矩阵中的元素会首先按列排列为一个列向量，再返回各元素在该列向量中的位置
     E=[1 0;3 0;5 0];find(E)
% ③对矩阵使用时如果需要返回行列信息，则使用两个参数接收即可：[row,col]=find（矩阵名，个数）（默认为全部元素），返回两个列向量
     E=[1 0;3 0;5 0];[A,B]=find(E,3)

% 15.矩阵中元素与常数的大小关系判断：使用 == > < ~= 即可以完成每个元素的关系判断，返回一个逻辑矩阵（1代表成立，0代表不成立）
     E=[1 -1;2 -2;3 -3];E>0
     
% 16.判断语句if的使用：语法：if 条件语句（不需要加冒号）执行段...elseif 条件语句 执行段...else 执行段 end
     a=input("请输入一个数字：")
     if a>90
         disp("优")
     elseif a>=60
         disp("合格")
     else
         disp("不及格")
     end
     
% 17.循环语句
% ①while语句：语法：while 条件表达式 循环体... end
    i=1;
    while i<10
        i=i+1
    end
% ②for语句：语法：for 变量名=表达式1：表达式2：表达式3 end |表达式1是初值条件，表达式2为公差（默认为1），表达式3为终止值（过了该值循环终止）
    for i=1:10
        disp(i)
    end
    
% 18.switch语句：语法：switch 变量名 case 常量1 语句序列1；case 常量2 语句序列2；...otherwise 语句序列; end 
%    这些case语句之后不用接break语句
     num=input("")
     switch num
         case 1
             disp("输入为1")
         case 2
             disp("输入为2")
         case 3
             disp("输入为3")
         otherwise
             disp("输入为其他值")
     end

%% 第二节课:TOPSIS方法与熵权法修正

% 1.生成与加载mat文件的语句：
%   生成由Excel产生的mat文件：在工作区新建一个变量，将Excel表格中对应的矩阵复制到变量中，然后将变量另存为mat文件即可
%   加载mat文件：要求mat文件与代码的m文件在同一个文件夹中，使用load mat文件名即可
% 2.逻辑运算：逻辑运算符分别为 &（与） |（或） ~（非）
    a=1;a==1&a==0
    a=1;a==1|a==0
    a=1;a~=0
% 3.幻方矩阵magic（）：语法：magic(n) 返回一个幻方矩阵（要求n不小于三）：一个元素由1排到n平方的方阵，且该方阵每一列的和都相等
    magic(3)
% 4.排序函数sort（）：可以对向量和矩阵使用，效果略有不同
% ①向量排序：sort(向量名，排序方式）：默认采用升序排序，如果要使用降序排序则使用'descend'作为第二个参数即可。
%   可以直接使用，也可以返回两个参数[vector,index]，其中vector是排序后的向量，index是排序之前的索引
    E=[1 2 3 4 5];[V,I]=sort(E,'descend')
% ②矩阵排序：sort（矩阵名，维度）：维度为1时，对每一列升序排序，维度为2时，对每一行升序排序
    E=magic(5);sort(E,2)
% 5.自定义函数：自定义的函数必须要单独放在一个m文件中
% 函数定义方式：function [输出变量] = 函数名（输入变量）...函数体... end  其中输入变量和输出变量都可以有多个
% 使用函数的m文件需要和函数文件在同一个文件夹中，使用时无需额外声明
% 6.zeros（）和ones（）函数：zeros（m,n)可以构造一个m行n列的元素均为0的矩阵，ones(m,n)可以构造一个m行n列的元素均为1的矩阵
    zeros(3,2)
    ones(2,3)
% 7.圆周率的表示：直接用 pi 表示即可
    pi
% 8.常用三角函数sin（）与cos（）：直接使用即可
    x=1:10;
    sin(x)
    cos(x)

%% 第三节课：插值算法

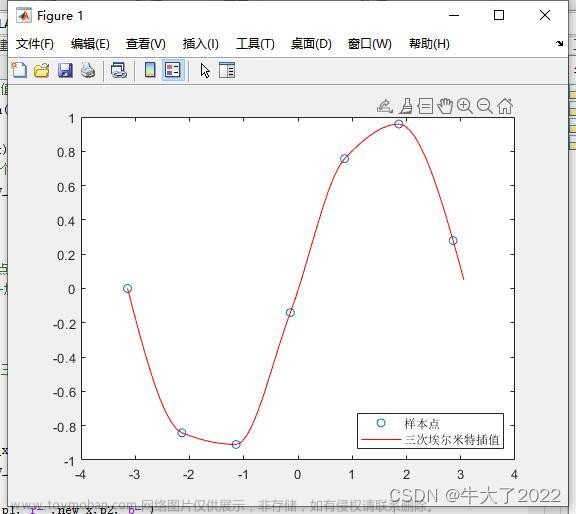
% 1.三次埃尔米特插值函数pchip（）:语法：pchip(x,y,new_x)，其中x,y分别为已知顶点的横纵坐标向量，new_x是插入结点的横坐标向量
    x=-pi:pi;y=sin(x);new_x=-pi:0.1:pi;
    new_y=pchip(x,y,new_x)
    
% 2.作图函数plot（）：
% ①直接使用：plot（x,y,颜色+线方式+点方式）:x和y分别为横坐标向量和纵坐标向量，作出函数图像，可以指定连线方式，节点形式和线的颜色
%   线的形式：-实线 ：点线 -.虚点线 --波折线  点的形式：.圆点 +加号 *星号 xX形 o小圆  颜色：y黄 r红 g绿 b蓝 w白 k黑 m紫 c青
%   如果参数中不注明线的方式，则可以画出散点图
    x=-pi:pi;y=sin(x);
    plot(x,y,'r--x')
% ②可以将多个函数的图像画在同一张图中：将参数分为多组即可
    x1=-pi:pi;y1=sin(x);
    x2=-pi:pi;y2=cos(x);
    plot(x1,y1,'r--x',x2,y2,"b-.+")
% ③关闭所绘制的图像：使用close命令即可
    close;

% 3.三次样条插值函数spline()：语法与pchip()函数的语法完全相同，但是插值的方式属于样条插值，样条插值更加圆滑
     x=-pi:pi;y=sin(x);new_x=-pi:0.1:pi;
     new_y=spline(x,y,new_x)
     
% 4.图例函数legend（）：与plot函数搭配使用，能够标出plot中每组函数数据的名称作为图例，图例的位置选择性可调
%   plot（第一组xy，第二组xy...第n组xy）；legend（名称1，名称2...名称，'Location',位置）
    x=-pi:0.1:pi;
    y1=sin(x)
    y2=cos(x)
    plot(x,y1,x,y2)
    legend("正弦函数","余弦函数",'Location','SouthEast')
    
% 5.figure（）函数的作用：给每一张图像标号，防止新生成的图像覆盖原有的图像
    x=-pi:0.1:pi;
    y1=sin(x);
    y2=cos(x);
    figure(1);
    plot(x,y1,x,y2)
    legend("正弦函数","余弦函数",'Location','SouthEast');
    figure(2)
    plot(x,tan(x))
    
% 6.n元函数插值函数interpn（）：语法：interpn（x1,x2...xn,y,new_x1,new_x2...new_xn,插值方法）
%   其中插值方法的选择最好使用三次样条插值"spline",其余使用方法与之前的插值函数类似
    x=-pi:pi;y=sin(x);new_x=-pi:0.1:pi;
    new_y=interpn(x,y,'spline')
    
% 第四节课：拟合算法

% 1.给坐标轴命名的xlabel()函数和ylabel()函数：与plot函数配合使用，可以在图中标出x轴与y轴的名字
    x=1:10;y=sin(x);
    plot(x,y)
    xlabel("自变量");ylabel("因变量");
    
% 2.hold on命令和grid on命令：hold on命令在使用一次plot函数后，表示下一次作图仍然在该图中;grid on命令可以显示网格线
    x=1:10;y=sin(x);
    plot(x,y)
    hold on;
    grid on;
    plot(x,x)
    
% 3.匿名函数的使用方法：函数名 = @（参数列表）表达式  调用方法：函数名（参数列表）
    z=@(x,y)x^2+y^2;
    z(1,2)
%   一元匿名函数的作图可以使用fplot（）函数：语法：fplot（匿名函数名，[a,b]），其中[a,b]表示作图区间
    z=@(x)x^2+5;
    fplot(z,[-5,5])
    
% 4.曲线拟合工具箱Curve Fitting的使用：可以从APP处进入，也可以使用命令：cftool 进入
    cftool;
%   获取x,y向量（二元函数中还要获取z向量）并选择拟合方式后，即可开始拟合，自动计算出拟合的参数和参茶和、拟合优度等内容
%   有时拟合偏差过大，需要在拟合设置中调整变量的初始点使其能够收敛，成功实现拟合，在拟合成功后可以导出拟合函数图像和拟合代码供自己使用
%   注意：导出拟合函数图像时，选择最高的分辨率，这样得到的图像最为清晰
    load data1.mat;
    cftool;

% 5.随机数和随机矩阵的生成：包括均匀随机分布和正态随机分布
% ①均匀随机分布的整数矩阵生成：randi（[a,b],m,n）：生成一个m*n的矩阵，矩阵中的元素为从a到b的整数
    randi([-10,10],3,4)
% ②均匀随机分布的小数矩阵生成：rand（m,n）：生成一个m*n的矩阵，矩阵中的元素为0到1之间的小数
    rand(2,3)
% ③正态随机分布的随机矩阵的生成：normrad（a,b,m,n）：生成一个元素均值为a，标准差为b，m*n的矩阵
    normrnd(0,1,5,6)
% ④一定范围内的随机数的生成：unifrnd(a,b,m,n)：a和b表示随机数的区间，m和n表示生成矩阵的大小
    unifrnd(-1,1,3,3)
% ⑤一定均值的指数分布的随机数的生成：exprnd(x)：x表示均值的大小
    exprnd(3)
    
% 6.四舍五入函数roundn：语法：round（变量名，位数） 可以在指定位数处进行四舍五入操作（个位用0表示）
    a=3.1415926;roundn(a,-3)

%% 第五节课：相关系数

% 1.常用的统计量函数：min/max()：求最小值/最大值  mink/maxk()：求k个最小元素/最大元素  bounds()：最小元素和最大元素
% mean()：求均值  median()：求中位数  mode()：求众数  std()：求标准差  var()：求方差
% skewness()：求偏度  kurtosis()：求峰度  topkrows():求按排序顺序的前k行
% 以上的统计量函数均默认按照列计算，如果需要按照行计算需要将第二个参数设置为2
Matrix_test=randi([-100,100],5,6);
min(Matrix_test)
max(Matrix_test)
bounds(Matrix_test)
mean(Matrix_test)
median(Matrix_test)
mode(Matrix_test)
std(Matrix_test)
var(Matrix_test)
skewness(Matrix_test)
kurtosis(Matrix_test)

% 2.皮尔逊相关系数的计算函数corrcoef（）的两种用法：
% ①corrcoef(A)：A是一个矩阵，其中每行表示每个样本，每列表示每个指标，返回一个对称矩阵，表示每两个指标之间的皮尔逊相关系数
  A=randi([-5,5],5,6);
  corrcoef(A)
% ②corrcoef(A,B)：A、B为两个向量，返回A和B的相关系数
  A=randi([-5,5],1,10);B=randi([-5,5],1,10);
  corrcoef(A,B)
% 另外，该函数还可以返回P值，用两个参数接收结果即可：语法:[R,P]=corrcoef(矩阵名），其中R为相关系数表，P为P值表
  
% 3.t分布概率密度函数tpdf()与概率分布函数tcdf（）以及t分布的概率分布函数的反函数tinv（）：
% ①概率密度函数：语法：tpdf（横坐标向量，自由度）
  x=-5:0.1:5;
  y=tpdf(x,28);
  plot(x,y)
% ②概率分布函数：语法：tcdf（横坐标，自由度）
  tcdf(3.055,28)
% ③概率分布函数的反函数（用于求t分布的临界值）:语法：tinv(概率值,自由度)
  tinv(0.975,28)
  
% 4.JB（雅克贝拉）检验函数jbtest（）的使用：语法：jbtest（样本值向量，显著性水平）
% 当输出为0时表示满足正态分布，输出为1时表示不满足正态分布
  x=normrnd(0,1,1,100);
  jbtest(x,0.05)
% 也可以有两个输出值，用[h,p]接收，分别表示判断结果和p值

% 5.Q-Q图作图函数qqplot（）：语法：qqplot（样本值向量）
   x=normrnd(0,1,1,1000);
   qqplot(x)
% 6.斯皮尔曼相关系数的计算函数corr（）的两种使用：
% ①corr（矩阵名，'type','Spearman')：计算矩阵各列之间的斯皮尔曼相关系数
  x=randi([-10,10],5,6);
  corr(x,'type','Spearman')
% ②corr(向量1，向量2，'type','Spearman')：计算两个向量之间的斯皮尔曼相关系数（注意：只能是列向量）
  x=randi([-10,10],100,1);y=2*x;
  corr(x,y,'type','Spearman')
% Matlab中所计算出来的斯皮尔曼相关系数实际上是等级的皮尔逊相关系数

% 7.正态分布的概率分布函数normcdf（）：语法：normcdf（概率值）
  normcdf(0.95)
  
%% 第六节课：图论中的最短路径问题

% 1.Matlab无向图图函数graph()与有向图图函数digraph()：
% ①当参数个数为两个时，语法为：graph/digraph（s,t）
%   其中s和t分别为两个点集，其中的元素个数要求相同，可以是从1开始的一系列整数，也可以是用大括号封闭的一个元胞数组（其中元素为字符串）
  s=[1,2,3,4];t=[4,3,2,1];
  G1=graph(s,t);figure(1);plot(G1)
  G2=digraph(s,t);figure(2);plot(G2)
% ②第三个参数为边的权重（默认每条边的权重为1），是一个与点集元素个数相同的数组，画图时标出权重的方式：plot(图名，'Edgelabel',图名.Edges.Weight)
   s=[1,2,3,4];t=[4,3,2,1];w=[1,2,3,4];
   G=graph(s,t,w);plot(G,'Edgelabel',G.Edges.Weight)

% 2.隐藏坐标轴名称的方法（与plot函数搭配使用）：set（gca，'XTick',[],'YTick',[])
  s=[1,2,3,4];t=[2,3,4,1];w=[1,2,3,4];
  G=graph(s,t,w);plot(G,'Edgelabel',G.Edges.Weight)
  set(gca,'XTick',[],'YTick',[]);
  
% 3.求最短路径的函数shortestpath（）：语法：shortestpath(图变量名，起点，终点,['Method',算法])
% 其中的图可以是无向图或者有向图，最后的算法是可选参数，默认采用自动选择的方式，输出两个参数，分别表示最短路径经过的结点和最短路径长度
% 可选的算法有：unweighted：广度优先计算（将所有边的权重均视为1） positive：迪杰斯特拉算法，要求边的权重均为非负数
%               mixed：贝尔曼-福特算法，效率比迪杰斯特拉算法低，但是适用范围更广。
  s=[1,2,3,4];t=[2,3,4,1];w=[1,2,3,4];G=graph(s,t,w);
  [path,length]=shortestpath(G,1,3)

% 4.高亮标出最短路径的方式：使用函数highlight()：语法：highlight（图像名，最长路径名，’EdgeColor',颜色）
  s=[1,2,3,4];t=[2,3,4,1];w=[1,2,3,4];G=graph(s,t,w);
  [path,length]=shortestpath(G,1,3);
  Plot=plot(G,'linewidth',3);highlight(Plot,path,'EdgeColor','r')
  
% 5.求任意两点之间的最短距离的矩阵的函数distances()：语法：distances（图名，['Method',算法]）
  s=[1,2,3,4];t=[2,3,4,1];w=[1,2,3,4];G=graph(s,t,w);
  distances(G)
  
% 6.找出给定距离范围内的所有节点的函数nearest()：语法：nearest（图名，结点，距离，['Method',算法]）
%   返回两个列向量[Nodes,Dists]，分别表示满足条件的结点以及它们所对应的最短距离
   s=[1,2,3,4];t=[2,3,4,1];w=[1,2,3,4];G=graph(s,t,w);
   [Nodes,Dists]=nearest(G,1,5)

% 7.输出警告信息的函数warning():语法：warning（警告提示字符串）
  warning("输入错误，请重新输入！")

% 8.用于退出函数的return语句：在自定义函数的定义体中使用，可以直接退出当前函数
  return

% 9.记录程序运行时间的方法
  tic;  %开始计时
  toc;  %停止计时
  
% 10.修改Matlab数字计算结果的格式为长数字形式（不使用则采用默认的四位小数或科学计数法形式）
  format long g
  
% 11.无穷大数字的表示方法
  inf
  
% 12.求两个整数相除的余数
% mod(被除数,除数)
mod(100,14)

% 13.设置绘图中横轴和纵轴的范围
% axis([x1 x2 y1 y2])：其中x1表示x的下限，x2表示x的上限；y1表示y的下限，y2表示y的上限
x=1:0.01:3;
y=2*x;
plot(x,y)
axis([1 4 2 8]);

% 14.设置程序暂停
% pause(暂停时间)：暂停时间用秒计算
pause(3)

% 15.在图中指定坐标处标注文本
% text(横坐标,纵坐标,文本内容)
text(2,4,"示例");


%% 数学规划问题

% 1.线性规划函数：linprog函数
% [x,fval]=linprog(C,A,B,Aeq,Beq,lb,ub,xo)
% 其中C表示线性目标函数的参数向量（列向量）；A表示不等式约束条件构成的矩阵；B表示不等式约束条件的右边部分构成的向量；
% Aeq和Beq分别表示等式约束条件的矩阵和右边部分构成的向量；lb和ub分别表示决策变量的上下界向量；xo表示迭代求解的初始值（线性规划一般不用给）
% 注意事项：
% ①该函数默认求解的是决策函数的最小值，如果求最大值需要取相反数处理；
% ②如果哪一个约束不存在，可以使用 [] 进行代替
% ③所有不等式约束的不等条件均为小于等于，如果是大于等于则需要左右两边同时取相反数处理
% ④返回值中x表示最优解时x的取值向量，而fval表示最优解的值
% ⑤不是所有的数学规划问题都有最优解，有可能无解或有无穷多个解

% 例题1：
C=[-5,-4,-6]';
A=[1 -1 1; 3 2 4; 3 2 0];
B=[20 42 30]';
lb=[0 0 0]';
[x,fval]=linprog(C,A,B,[],[],lb)

% 例题2：
C=[0.04 0.15 0.1 0.125]';
A=[-0.03 -0.3 0 -0.15;0.14 0 0 0.07];
B=[-32,42]';
Aeq=[0.05 0 0.2 0.1];
Beq=[24];
lb=[0 0 0];
[x,fval]=linprog(C,A,B,Aeq,Beq,lb,[])

% 例题3：
C=[-2 -3 5];
A=[-2 5 -1;1 3 1];
B=[-10 12]';
Aeq=[1 1 1];
Beq=[7];
lb=[0 0 0];
[x,fval]=linprog(C,A,B,Aeq,Beq,lb,[])
fval=-fval


% 2.线性整数规划函数：intlinprog函数
% [x,fval]=linprog(C,intcon,A,B,Aeq,Beq,lb,ub,xo)
% 该函数与线性规划函数仅多了参数intcon，少了参数xo，其中intcon表示哪些决策变量要求取整数
% 可以利用intlinprog函数求解0-1线性规划问题（设置上界和下界即可）

% 例题1：
C=[-5,-4,-6]';
A=[1 -1 1; 3 2 4; 3 2 0];
B=[20 42 30]';
lb=[0 0 0]';
[x,fval]=intlinprog(C,[1 2 3],A,B,[],[],lb)

% 例题2：
C=[-20 -10]';
intcon=[1 2];
A=[5 4;2 5];
B=[24 13];
lb=[0 0]
[x,fval]=intlinprog(C,intcon,A,B,[],[],lb,[])
fval=-fval

% 例题3：
C=[18 23 5]';
intcon=[3];
A=[107 500 0;-107 -500 0;72 121 65;-72 -121 -65];
B=[50000 -500 2250 -2000]';
lb=[0 0 0];
[x,fval]=intlinprog(C,intcon,A,B,[],[],lb,[])

% 例题4：
C=[-3 -2 -1]';
intcon=[3];
A=[1 1 1];
B=[7];
Aeq=[4 2 1];
Beq=[12];
lb=[0 0 -inf];
[x,fval]=intlinprog(C,intcon,A,B,Aeq,Beq,lb,[])

% 3.非线性规划函数求解：fmincon函数
% [x,fval]=fmincon(@func,x0,A,B,Aeq,beq,lb,ub,@nonlfun,option)
% 1.x0表示迭代的初始值。非线性规划问题的初始值非常重要，不可以省略。
% 2.该函数求解出的是局部最优解而不是全局最优解，如果需要求解全局最优解则可以尝试多组初始值选择最优解，或者使用蒙特卡洛模拟再代入初始值
% 3.option选项可以选择求解使用的算法，一般可以忽略，建议所有方法使用一次选择最优的方法。
% 四种可选方法分别为：interior_point（内点法） sqp（序列二次规划法） active-set（有效集法）
% trust-region-reflective（信赖域反射算法）
% option=optimoptions('fmincon','Algorithm',算法名称)
% 4.@fun表示目标函数，需要专门用一个m文件进行存储；@nunlfun表示非线性约束条件，同样需要使用一个单独的m文件进行存储
% 5.非线性不等式约束的右边只能为0

% 例题1：
x0=[0 0];
A=[-2 3];
B=[6];
option=optimoptions('fmincon','Algorithm','sqp');
[x,fval]=fmincon(@fun1,x0,A,B,[],[],[],[],@nonlfun1)

% 4.最大最小化规划问题求解：fminimax函数
% （由于使用次数较少，因此使用过程略）

%% 附加部分：粒子群算法函数：particleswarm
% 注意事项：该算法只能用于求最小值，如果求最大值则需要取相反数
% 使用语法：[自变量最佳取值,最优解,返回标志,结构体]=particleswarm(@目标函数名,变量个数,自变量下界,自变量上界,可选项)
% 返回标志：返回标志为从1-6的六种，分别表示不同的返回情况
% 结构体：结构体中含有迭代次数的信息
% 可选项：可选项中的参数可以实现绘制出局部最优解随迭代次数变化的图像
narvs=2;
x_lb=[-15 -15];
x_ub=[15 15];
% 可选项中分别表示：①绘制迭代过程；②将粒子数设置为50个以提高精确的（默认为10个）；③调用其他函数帮助共同求解以提高精确度
options=optimoptions('particleswarm','PlotFcn','pswplotbestf','SwarmSize',50,'Hybrid',@fmincon);
[x,fval,exitflag,outputstruct]=particleswarm(@fun2,narvs,x_lb,x_ub,options)





%% 第十二节课 预测模型

% 1


% 第十三节课 奇异值分解与图形处理

% 1.矩阵的奇异值分解方法：[U,S,V]=svd(矩阵名)
A=magic(5);
[U,S,V]=svd(A)

% 2.向程序中导入图片文件：imread函数
% imread(图片完整路径名)
% 注意事项：在进行奇异值分解前需要将矩阵的元素类型转化为double型，方法为double(矩阵名)
test_photo=imread("C:\Users\86139\Pictures\Saved Pictures\test.jpg");

% 3.将彩色图片转化为灰色图片的函数：rgb2gray(导入的图片变量名)
test_photo=imread("C:\Users\86139\Pictures\Saved Pictures\test.jpg");
rgb2gray(test_photo)

% 4.提取图片矩阵变量的方法：
% 提取RGB红色、绿色、蓝色元素值构成的矩阵：图片名(:,:,1)、图片名(:,:,2)、图片名(:,:,3)

% 5.Matlab处理视频文件的方法
% ①向程序中导入视频文件：VideoReader(视频完整路径名)
% ②获取视频的总帧数：视频变量名.NumberOfFrames
% ③读出视频指定帧数的图像：read(视频变量名,帧数)
% ④保存处理后的图片：imwrite(图片变量名,图片保存完整路径名)

% 更新13：Matlab三维图形的绘制

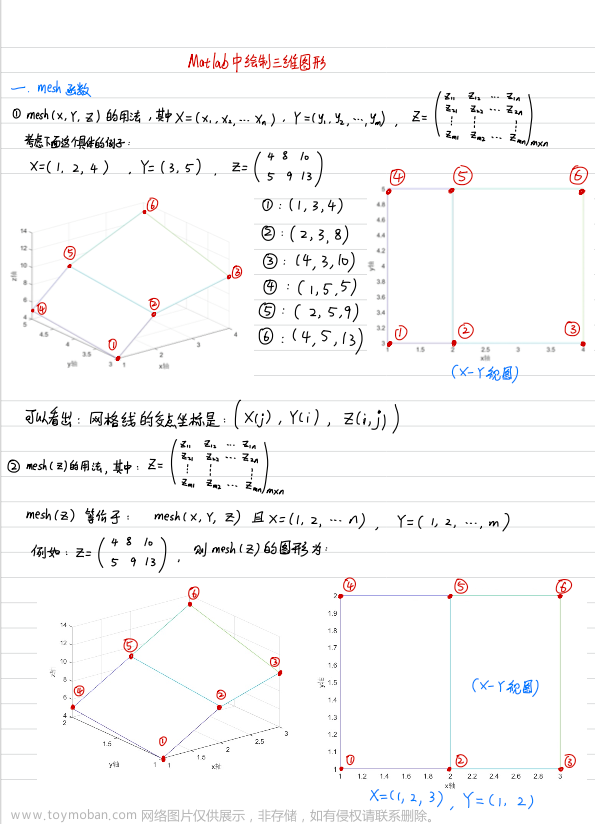
% 1.mesh函数：用于某一区间内三维完整网格图（由网格拼接产生的图）的绘制
% ①mesh（X,Y,Z）：其中X,Y,Z均为m*n的矩阵，则（X(i,j) Y(i,j),Z(i,j)）是网格线的交点、
% 插入颜色栏后可以显示色阶，向量中元素不按照大小顺序排列也可，网格图会发生翻折
  X=[1,2,4;1,2,4];Y=[2,2,2;1,1,1];Z=[4,8,10;5,9,13];
  mesh(X,Y,Z)
% 插入颜色栏后可以显示色阶，向量中元素不按照大小顺序排列也可，网格图会发生翻折
% ②可以用alpha函数设置透明度（0-1），透明度越接近1越不透明，或者直接用hidden off将透明度设置为完全透明
  Z=[4,8,10;5,9,13];
  mesh(Z)
  alpha(0.5);hidden off;

% 2.绘制三维曲面的等高线和底座的函数：meshc函数和meshz函数
% ①meshc函数：在mesh函数的基础上，在xOy平面上绘制等高线图
% meshc(x,y,z)：其中x y z表示的内容与mesh函数相同
[x,y]=meshgrid(-5:0.2,5);
z=x+y;
meshc(x,y,z);
% ②meshz函数：在mesh函数的基础上，在xOy平面上绘制曲面的底座

% 3.绘制带填充的网格图：surf函数
% surf函数的使用方法与mesh函数的使用方法完全相同，但是mesh是进行画线，surf则是直接进行曲面的绘制
% surf函数还有surfc和surfl两个函数，分别可以在xOy上绘制等高线以及加上灯光效果（更加好看一些）

% 4.绘制图像的子图效果：subplot函数
% subplot(行数,列数,位置)

% 5.绘制图形的等高线：contour函数
% contour(x,y,z)

% 6.符号函数的图形绘制（符号函数就是参数方程表示的函数）
% ①plot3函数：类似于plot函数，但是可以绘制出三维空间内的曲线图
x=1:0.01:5;
y=sin(x);
z=cos(x);
plot3(x,y,z);
% 使用close语句可以关闭所绘制的图像
% plot3函数也可以设置曲线的颜色、表现形式等等，设置方式与plot函数相同
% ②Matlab符号运算与相关函数图像绘制（相当于参数方程中的参数）
% 符号的定义方式：syms 符号名
% 符号函数的图像绘制：fplot3(x,y,z,[符号下限,符号上限])
syms t;
x=sin(t);
y=cos(t);
z=2*t;
fplot3(x,y,z,[-10 10]);
% 同样可以使用fmesh、fsurf等方式对符号函数的曲面进行绘制，此处不再赘述

% 7.隐函数的三维图像的绘制方法：fimplicit3
% fimplicit3(函数句柄,绘图区间)
% 函数句柄可以表示为：函数名=@(输入参数) 输出表达式 的形式

% Matlab的符号运算

% 1.符号变量的创建
% syms 符号变量名
% 注释：可以用一个syms语句同时创建多个变量
syms y;
syms a b;

% 2.符号方程的创建
% 符号方程可以理解为就是参数方程，右边部分为符号变量运算表达式的方程就是符号方程
syms a b;
c=a*a+b+a;

% 3.符号变量的简单运算
% 符号变量的运算与一般变量的运算相同

% 4.符号表达式的化简方法：simplify
% 化简语法：simplify(符号表达式)
syms a;
y=(cot(a/2)-tan(a/2))*(1+tan(a)*tan(a/2));
simplify(y)

% 5.因式分解功能：factor函数
% ①factor(常数)：表示对常数进行因式分解
factor(16)
% ②factor(符号表达式)：表示对符号表达式进行因式分解
syms m n;
y=m^3-n^3;
factor(y)

% 6.多项式展开函数和合并函数：expand函数和collect函数
% ①展开语法：expand(待展开符号多项式）
syms m;
y=m*(m*2-3*m*m);
z=expand(y)
% ②合并语法：collect(待合并符号多项式,需要合并的符号)
collect(z,m)

% 7.计算分子和分母的函数：numden函数
% 使用语法：[分子名,分母名]=numden(符号表达式)
[z1,z2]=numden(sym(2.5))
% 此处的sym函数的作用是将其他数据类型转换为符号

% 8.符号函数的求导：diff
% ①一元函数求导语法：diff(符号函数表达式,导数阶数)
syms x;
diff(cos(x),10)
% ②多元函数求导语法：diff(符号函数表达式,求导符号,导数阶数)
syms x y;
diff(x*x*x+y*y*y,y,3)
% 如果需要先对某个自变量求偏导数，再对另一个自变量求偏导数，则可以使用以下语法
% 语法：diff(符号函数表达式,第一个求导的符号,第二个求导的符号....)
diff(x*x*x+y*y*y,x,y)
% 注意事项：如果diff函数的作用对象不是符号函数表达式而是一个矩阵，那么其作用就是求差分

% 9.符号函数的积分计算
% ①不定积分的计算：int(符号函数表达式,被积分变量)
syms x;
y=x*x;
int(y,x)
% ②定积分的计算：int(符号函数表达式,被积分变量,积分下限,积分上限)
syms x;
y=x*x;
int(y,x,0,2)
% 注意：不是所有的符号函数都可以计算积分，对于一些符号函数只能计算数值积分（积分的近似值）
% 计算数值积分的语法：integral(符号函数表达式,被积分变量,积分下限,积分上限)

% 10.单变量和多变量方程、方程组求解：solve函数
% ①单变量方程求解语法：answer=solve(符号函数方程,待求解符号)
syms x;
answer=solve(sin(x)==1,x)
% 注意事项：符号函数方程的等式要用两个等号进行表示
% 对于周期函数，如果需要求解出所有解，那么需要对该函数使用附加参数
% ②多变量方程求解语法：与单变量方程求解相同，只是用其他变量来表示该变量
% ③方程组求解语法：answer=solve(多个方程构成的向量,待求解符号构成的向量)
syms x y;
answer=solve([x==2*y+1,y==2],[x,y]);
answer.x
answer.y

% 11.二维符号函数图像的绘制：fplot函数
% 使用语法：fplot(符号函数表达式,符号区间)
syms x;
fplot(sin(x),[-3,3])

% 12.指定解在指定区间内的方程：vpasolve函数
% 使用语法：vpasolve(符号方程表达式,求解变量,求解区间)
syms x;
vpasolve(sin(x)==1,x,[0,2])


% Matlab求解微分方程的解析解（也就是函数表达式）：dsolve函数
% 使用语法：dsolve(方程1,方程2...,初始条件,待求解自变量)
% 在微分方程中，用D表示一阶微分，用D2表示二阶微分，以此类推
% 初始条件可以省略
dsolve('y-Dy=2*x','x')

% 由于有些微分方程不存在解析解，因此只能退而求其次求出数值解：solver函数

到了这里，关于数学建模中所需要使用到的Matlab（从零开始介绍）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！