Gitee上开源的数据结构与算法代码库:数据结构与算法Gitee代码库
1. 概述
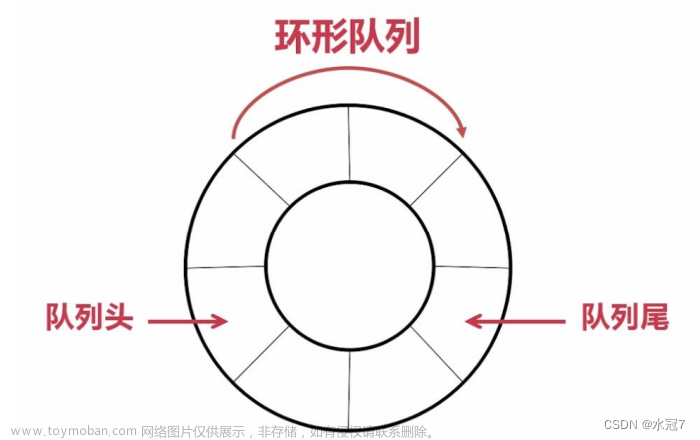
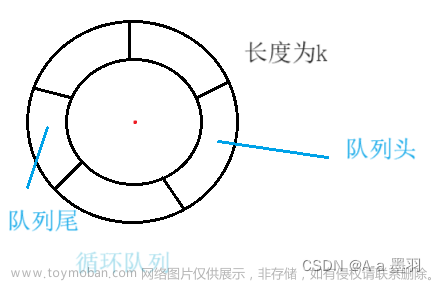
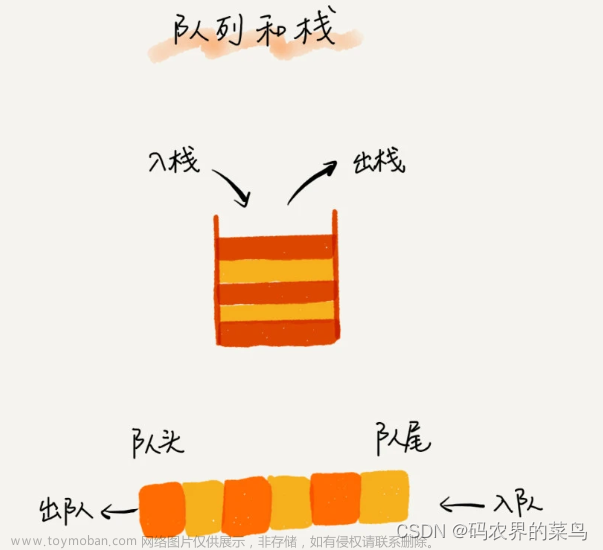
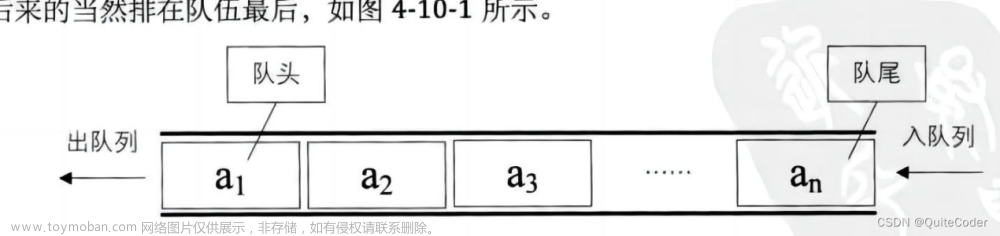
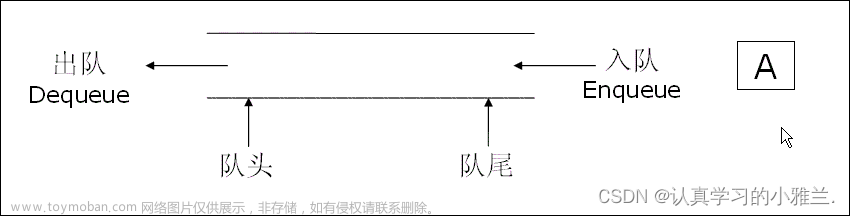
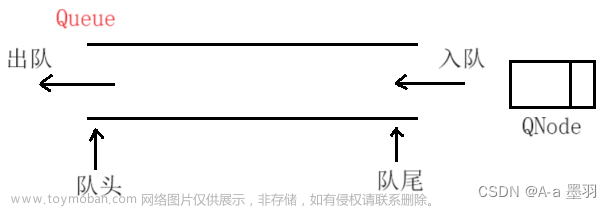
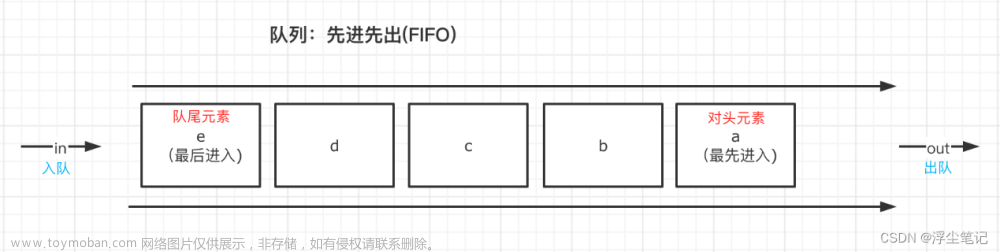
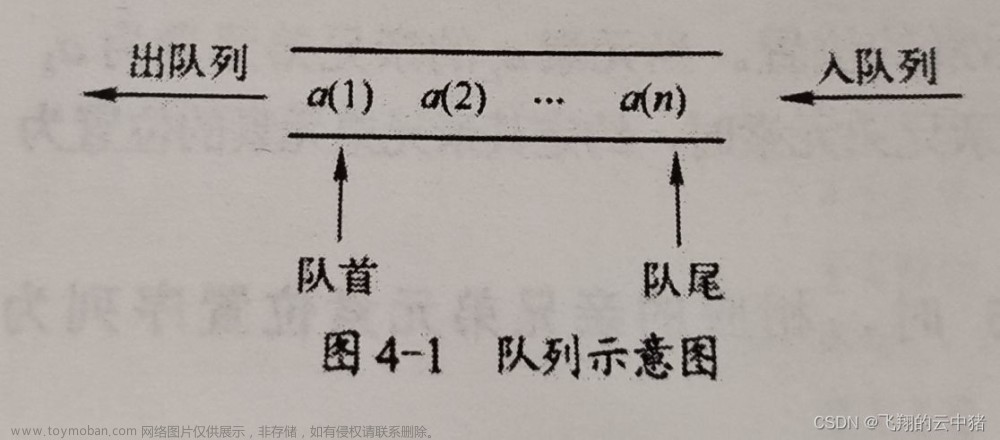
双端队列、队列、栈对比
| 定义 | 特点 | |
|---|---|---|
| 队列 | 一端删除(头)另一端添加(尾) | First In First Out |
| 栈 | 一端删除和添加(顶) | Last In First Out |
| 双端队列 | 两端都可以删除、添加 | |
| 优先级队列 | 优先级高者先出队 | |
| 延时队列 | 根据延时时间确定优先级 | |
| 并发非阻塞队列 | 队列空或满时不阻塞 | |
| 并发阻塞队列 | 队列空时删除阻塞、队列满时添加阻塞 |
注1:
- Java 中 LinkedList 即为典型双端队列实现,不过它同时实现了 Queue 接口,也提供了栈的 push pop 等方法
注2:
不同语言,操作双端队列的方法命名有所不同,参见下表
操作 Java JavaScript C++ leetCode 641 尾部插入 offerLast push push_back insertLast 头部插入 offerFirst unshift push_front insertFront 尾部移除 pollLast pop pop_back deleteLast 头部移除 pollFirst shift pop_front deleteFront 尾部获取 peekLast at(-1) back getRear 头部获取 peekFirst at(0) front getFront 吐槽一下 leetCode 命名比较 low文章来源:https://www.toymoban.com/news/detail-546972.html
常见的单词还有 enqueue 入队、dequeue 出队文章来源地址https://www.toymoban.com/news/detail-546972.html
2. 代码实现
a. 接口定义
/**
* 双端队列接口
* @param <E> 队列中元素类型
*/
public interface Deque<E> {
boolean offerFirst(E e);
boolean offerLast(E e);
E pollFirst();
E pollLast();
E peekFirst();
E peekLast();
boolean isEmpty();
boolean isFull();
}
b. 基于双向环形链表实现
public class LinkedListDeque<E> implements Deque<E>, Iterable<E> {
int capacity;
int size;
Node<E> sentinel = new Node<E>(null, null, null);
static class Node<E>{
Node<E> prev;
E value;
Node<E> next;
public Node(Node<E> prev, E value, Node<E> next) {
this.prev = prev;
this.value = value;
this.next = next;
}
}
public LinkedListDeque(int capacity) {
this.capacity = capacity;
sentinel.next = sentinel;
sentinel.prev = sentinel;
}
@Override
public boolean offerFirst(E e) {
if (isFull()){
return false;
}
Node<E> prev = sentinel;
Node<E> next = sentinel.next;
Node<E> added = new Node<>(prev, e, next);
prev.next = added;
next.prev = added;
size++;
return true;
}
@Override
public boolean offerLast(E e) {
if (isFull()){
return false;
}
Node<E> prev = sentinel.prev;
Node<E> next = sentinel;
Node<E> added = new Node<>(prev, e, next);
prev.next = added;
next.prev = added;
size++;
return true;
}
@Override
public E pollFirst() {
if (isEmpty()){
return null;
}
Node<E> a = sentinel;
Node<E> removed = sentinel.next;
Node<E> b = removed.next;
a.next = b;
b.prev = a;
size--;
return removed.value;
}
@Override
public E pollLast() {
if (isEmpty()){
return null;
}
Node<E> b = sentinel;
Node<E> removed = sentinel.prev;
Node<E> a = removed.prev;
a.next = b;
b.prev = a;
size--;
return removed.value;
}
@Override
public E peekFirst() {
if (isEmpty()){
return null;
}
return sentinel.next.value;
}
@Override
public E peekLast() {
if (isEmpty()){
return null;
}
return sentinel.prev.value;
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public boolean isFull() {
return size == capacity;
}
@Override
public Iterator<E> iterator() {
return new Iterator<E>() {
Node<E> p = sentinel.next;
@Override
public boolean hasNext() {
return p != sentinel;
}
@Override
public E next() {
E value = p.value;
p = p.next;
return value;
}
};
}
}
c. 基于双向环形链表实现
/**
* 基于循环数组实现 1
* 特点:
* - tail 停下来的位置不存储,会浪费一个位置
*/
public class ArrayDeque<E> implements Deque<E>, Iterable<E> {
/*
h - head
t - tail
offerLast() 先添加到tail的位置,tail++
offerFirst() head--, 添加到head的位置
pollFirst() 先获取要移除的值,head++
pollLast() 先tail-1,再获取值
head == tail 空
head ~ tail == 数组长度-1 满
*/
E[] array;
int head;
int tail;
@SuppressWarnings("all")
public ArrayDeque(int capacity) {
array = (E[]) new Object[capacity + 1];
}
/**
* 指针 + 1 越界换算
* @param i
* @param length
* @return
*/
static int inc(int i, int length){
if (i + 1 >= length){
return 0;
}
return i + 1;
}
/**
* 指针 - 1 越界换算
* @param i
* @param length
* @return
*/
static int dec(int i, int length){
if (i - 1 < 0){
return length - 1;
}
return i - 1;
}
@Override
public boolean offerFirst(E e) {
if (isFull()){
return false;
}
head = dec(this.head, array.length);
array[head] = e;
return true;
}
@Override
public boolean offerLast(E e) {
if (isFull()){
return false;
}
array[tail] = e;
tail = inc(tail, array.length);
return true;
}
@Override
public E pollFirst() {
if (isEmpty()){
return null;
}
E value = array[head];
array[head] = null; // help GC
head = inc(head, array.length);
return value;
}
@Override
public E pollLast() {
if (isEmpty()){
return null;
}
tail = dec(tail, array.length);
E value = array[tail];
array[tail] = null; // help GC
return value;
}
@Override
public E peekFirst() {
if (isEmpty()){
return null;
}
return array[head];
}
@Override
public E peekLast() {
if (isEmpty()){
return null;
}
return array[dec(tail, array.length)];
}
@Override
public boolean isEmpty() {
return head == tail;
}
@Override
public boolean isFull() {
if (tail > head){
return tail - head == array.length - 1;
} else if (tail < head){
return head - tail == 1;
} else {
return false;
}
}
@Override
public Iterator<E> iterator() {
return new Iterator<E>() {
int p = head;
@Override
public boolean hasNext() {
return p != tail;
}
@Override
public E next() {
E e = array[p];
p = inc(p, array.length);
return e;
}
};
}
}
到了这里,关于数据结构与算法-双端队列的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!