更多国赛数学建模资料思路，关注文末！
1 优劣解距离法（TOPSIS）简介
1.1 概念
TOPSIS 法是一种常用的组内综合评价方法，能充分利用原始数据的信息，其结果能精确地反映各评价方案之间的差距。基本过程为基于归一化后的原始数据矩阵，采用余弦法找出有限方案中的最优方案和最劣方案，然后分别计算各评价对象与最优方案和最劣方案间的距离，获得各评价对象与最优方案的相对接近程度，以此作为评价优劣的依据。该方法对数据分布及样本含量没有严格限制，数据计算简单易行
1.2 适用范围
评价对象得分，且各个指标值已知。
1.3 模型基本步骤
1.21 将原始数据矩阵正向化。也就是将那些极小型指标，中间型指标，区间型指标对应的数据全部化成极大型指标，方便统一计算和处理。
1.22 将正向化后的矩阵标准化。也就是通过标准化消除量纲的影响。
1.23 计算每个方案各自与最优解和最劣解的距离
1.24 根据最优解与最劣解计算得分并排序
2 案例介绍及操作
为了客观地评价各风景地点的性价比，根据风景、人文、拥挤程度、票价等因素对各风景地点进行评估。
风景和人文越高越好，这样的指标称为极大型指标（效益型指标）
拥挤程度和票价越少越好，这样的指标称为极小型指标（成本型指标）
2.1 原始数据同趋势化（一般选择指标正向化）
将极小型指标拥挤程度和票价正向化后得：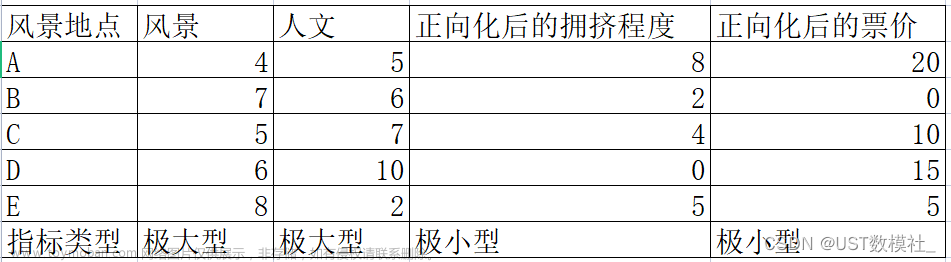
2.2 构建标准化矩阵
对该元素除以所在列的平方和再开根号：
经过标准化后得到：
2.3 计算各评价指标与最优及最劣向量之间的差距
定义第i个评价对象与最大值的距离：
定义第i个评价对象与最小值的距离：
指标权重可以使用熵权法或者层次分析法等方法确认。
D+和D-值的实际意义：评价对象与最优或最劣解的距离，值越大说明距离越远，研究对象D+值越大，说明与最优解距离越远；D-值越大，说明与最劣解距离越远。最理解的研究对象是D+值越小同时D-值越大。
对于上述数据，最大值【0.58，0.68，0.77，0.73】,最小值【0.29，0.14，0，0】,得到如下数据：
2.4 评价对象与最优方案的接近程度
D-值相对越大，则说明该研究对象距离最劣解越远，则研究对象越好；C值越大， 表明评价对象越优
文章来源：https://www.toymoban.com/news/detail-551840.html
由上表可知，景点 A 的综合评价最高，说明综合评估风景、人文、拥挤程度、票价后，景点 A 的性价比较高，距离负理想解相对远，距离正理想解相对近。其次是D、E、C、B。文章来源地址https://www.toymoban.com/news/detail-551840.html
到了这里，关于2023数学建模国赛常用算法-Topsis优劣解距离法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
