问题描述
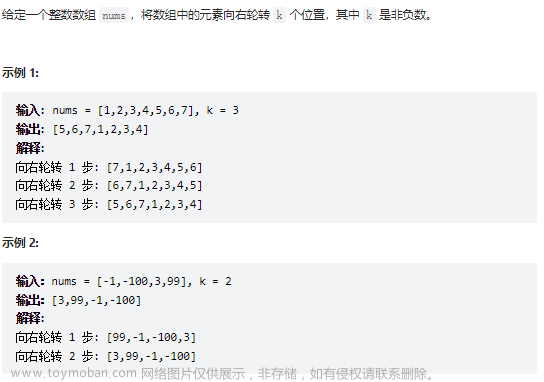
一个下标从 0 开始的数组的 交替和 定义为 偶数 下标处元素之 和 减去 奇数 下标处元素之 和 。 比方说，数组 [4,2,5,3] 的交替和为 (4 + 5) - (2 + 3) = 4 。
给你一个数组 nums ，请你返回 nums 中任意子序列的 最大交替和 （子序列的下标 重新 从 0 开始编号）。 一个数组的 子序列 是从原数组中删除一些元素后（也可能一个也不删除）剩余元素不改变顺序组成的数组。比方说，[2,7,4] 是 [4,2,3,7,2,1,4] 的一个子序列（加粗元素），但是 [2,4,2] 不是。
示例 1
输入：nums = [4,2,5,3]
输出：7
解释：最优子序列为 [4,2,5] ，交替和为 (4 + 5) - 2 = 7 。
示例2
输入：nums = [5,6,7,8]
输出：8
解释：最优子序列为 [8] ，交替和为 8 。
示例3
输入：nums = [6,2,1,2,4,5]
输出：10
解释：最优子序列为 [6,1,5] ，交替和为 (6 + 5) - 1 = 10 。
提示
- 1 <= nums.length <= 105
- 1 <= nums[i] <= 105
思路分析
-
首先， 定义数组 dp0 和 dp1，长度都为 n，并将它们初始化为全零数组。dp0[i] 表示从 nums[0] 到 nums[i] 的子数组中，以 nums[i] 结尾的交替和的最大值；dp1[i] 表示从 nums[0] 到 nums[i] 的子数组中，以 nums[i] 结尾的交替和末尾为正数的最大值。
-
然后，我们开始迭代遍历数组 nums，从索引 1 开始。在每次迭代中，我们根据以下公式更新 dp0 和 dp1 的值：
dp0[i] = max(dp0[i - 1], dp1[i - 1] - nums[i])
dp1[i] = max(dp1[i - 1], dp0[i - 1] + nums[i])
-
对于 dp0[i]，我们有两个选择：要么不选择当前元素 nums[i]，即交替和不变；要么将前一个交替和末尾的正数减去当前元素 nums[i]，以得到更大的交替和。所以，dp0[i] 的值可以通过比较 dp0[i-1] 和 dp1[i-1] - nums[i] 的大小来确定，取其中较大的值作为 dp0[i] 的结果。
-
对于 dp1[i]，同样有两个选择：要么不选择当前元素 nums[i]，即交替和末尾为正数的最大值不变；要么将前一个交替和末尾的负数加上当前元素 nums[i]，以得到更大的交替和。所以，dp1[i] 的值可以通过比较 dp1[i-1] 和 dp0[i-1] + nums[i] 的大小来确定，取其中较大的值作为 dp1[i] 的结果。
-
通过不断更新 dp0 和 dp1 数组的值，我们就可以得到从 nums[0] 到 nums[i] 的子数组中，以 nums[i] 结尾的交替和的最大值和交替和末尾为正数的最大值。
-
最后， 返回 dp0[n - 1] 和 dp1[n - 1] 中的较大值，即为所求的交替元素和的最大值。
代码分析
代码实现了一个计算交替元素和的最大值的函数
maxAlternatingSum。
class Solution(object):
def maxAlternatingSum(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
首先，这是一个名为 Solution 的类定义，它实现了一个方法 maxAlternatingSum。该方法接受一个参数 nums，它是一个整数列表，并且返回一个整数作为结果。
n = len(nums)
dp0 = [0] * n
dp1 = [0] * n
接下来，通过获取数组 nums 的长度 n，创建了两个与 nums 相同长度的全零数组 dp0 和 dp1，用于存储中间计算的结果。
dp1[0] = nums[0] # 初始化
将 dp1 的首元素设置为 nums 的首元素，作为初始值。
for i in range(1, n):
dp0[i] = max(dp0[i - 1], dp1[i - 1] - nums[i])
dp1[i] = max(dp1[i - 1], dp0[i - 1] + nums[i])
然后，使用一个循环从索引 1 开始遍历数组 nums，对每个位置 i 进行动态规划计算。根据之前解释的公式，更新 dp0[i] 和 dp1[i] 的值。
return max(dp0[n - 1], dp1[n - 1])
最后，返回 dp0 和 dp1 中的最大值作为结果。
代码的核心思想是使用动态规划来求解交替元素和的最大值。通过迭代计算并更新
dp0和dp1数组中的值，最终得到结果。
完整代码
class Solution(object):
def maxAlternatingSum(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
# 创建Solution类，定义maxAlternatingSum方法，该方法接受整数列表nums作为参数，返回一个整数作为结果
n = len(nums)
# 获取整数列表nums的长度，即列表中元素的数量
dp0 = [0] * n
dp1 = [0] * n
# 创建两个初始长度为n的全零列表dp0和dp1，用于记录中间计算结果
dp1[0] = nums[0]
# 将dp1列表的第一个元素设置为nums列表的第一个元素，作为初始化值
for i in range(1, n):
# 循环从索引1开始遍历整数列表nums
dp0[i] = max(dp0[i - 1], dp1[i - 1] - nums[i])
# 在位置i不选择当前元素时，最大交替和为前一个位置不选择元素的最大交替和dp0[i-1]和dp1[i-1]减去当前元素nums[i]的较大值
dp1[i] = max(dp1[i - 1], dp0[i - 1] + nums[i])
# 在位置i选择当前元素时，最大交替和为前一个位置选择元素的最大交替和dp1[i-1]和dp0[i-1]加上当前元素nums[i]的较大值
return max(dp0[n - 1], dp1[n - 1])
# 返回dp0和dp1列表中最后一个元素的较大值作为结果，即表示在最后一个位置不选择当前元素和选择当前元素两种情况下的最大交替和
运行示例代码
示例1
nums = [4, 2, 5, 3]
solution = Solution()
result = solution.maxAlternatingSum(nums)
print(result)
示例2
nums = [5,6,7,8]
solution = Solution()
result = solution.maxAlternatingSum(nums)
print(result)
示例3
nums = [6,2,1,2,4,5]
solution = Solution()
result = solution.maxAlternatingSum(nums)
print(result)
文章来源：https://www.toymoban.com/news/detail-552000.html
完结
文章来源地址https://www.toymoban.com/news/detail-552000.html
到了这里，关于【力扣算法05】之 _1911_ 最大子序列交替和- python的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
