【洛谷】P1576 最小花费（最短路---＞最长路（通过改边权变定义)）-Toy模板网

这篇具有很好参考价值的文章主要介绍了【洛谷】P1576 最小花费（最短路---＞最长路（通过改边权变定义)）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

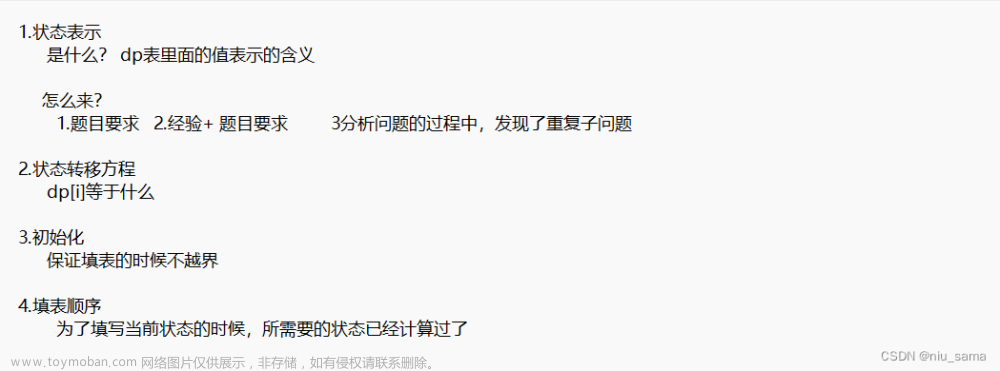
分析+变动+ACcode

明确定位最短路，其实就是模板加上稍微改动。

变动位置：

1：把权变成汇率（<=1.0），即经过了这条边，前就要乘以这这边权，即乘以汇率，拿肯定汇率越高最后到终点的钱多（一个道理终点钱指定，拿汇率越高，最开始的钱就可以拿的越少）。我们需要在松弛操作时找尽可能长的边，同时把运算符“<”重载成“>”，保证找到的路径最长.

那就把最短路--->求最长路

dis[a]=1.0;//代表汇率

e[++cnt].dis=1.0-d/100.0;//变成汇率

(当然这可以直接是dis=d/1.00),那就还是求最短路，就到终点权值相乘的最小值（这题独特在我们之前的权值都是加的，这题是乘的）（if(dis[j]<dis[t]*e[i].dis)）

2：dis[t]*e[i].dis是乘不是加

if(dis[j]<dis[t]*e[i].dis) { //注意这里是发现更大的dis时更新！！！
				dis[j]=dis[t]*e[i].dis;
				q.push((node){dis[j],j});
			}

3：那么，刚开始初始化就要为0

void init() { //初始化
	for(int i=1; i<=n; i++)
		dis[i]=0;   //注意不要设置成正无穷！！！
}

ACcode:

#include <bits/stdc++.h>
using namespace std;
struct edge {
	int to,nxt;
	double dis;
} e[200010];
struct node {//重载 
	double dis;
	int pos;
	bool operator <(const node &x)const {
		return x.dis>dis;  //注意重载成大于！！！，就是优先队列用less
	}
};

double head[4010],dis[4010];
bool vis[200010];
int n,m,s,cnt,a,b;

void addedge(int u,int v,int d) { //建边
	e[++cnt].dis=1.0-d/100.0;//变成汇率 
	e[cnt].to=v;
	e[cnt].nxt=head[u];
	head[u]=cnt;
}
priority_queue<node>q;
void init() { //初始化
	for(int i=1; i<=n; i++)
		dis[i]=0;   //注意不要设置成正无穷！！！
}
void dijkstra() {  //优先队列优化的dijkstra
	dis[a]=1.0;//代表汇率
	q.push((node) {1.0,a});
	while(!q.empty()) {
		int t =q.top().pos;
		q.pop();
		if(vis[t])continue;
		vis[t]=1;
		for(int i=head[t]; i; i=e[i].nxt) {
			int j=e[i].to;
			if(dis[j]<dis[t]*e[i].dis) { //注意这里是发现更大的dis时更新！！！
				dis[j]=dis[t]*e[i].dis;
				q.push((node){dis[j],j});
			}
		}
	}
}
int main() {
	scanf("%d%d",&n,&m);
	init();
	for(int i=1; i<=m; i++) {
		int u,v,d;
		scanf("%d%d%d",&u,&v,&d);
		addedge(u,v,d);
		addedge(v,u,d);  //注意建边2次！！！
	}
	scanf("%d%d",&a,&b);
	dijkstra();
	printf("%.8lf",100.0/dis[b]);  //注意是100/dis[b]
	return 0;
}

over~文章来源地址https://www.toymoban.com/news/detail-553001.html

到了这里，关于【洛谷】P1576 最小花费（最短路---＞最长路（通过改边权变定义)）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！