综合评价与决策方法-Toy模板网

这篇具有很好参考价值的文章主要介绍了综合评价与决策方法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

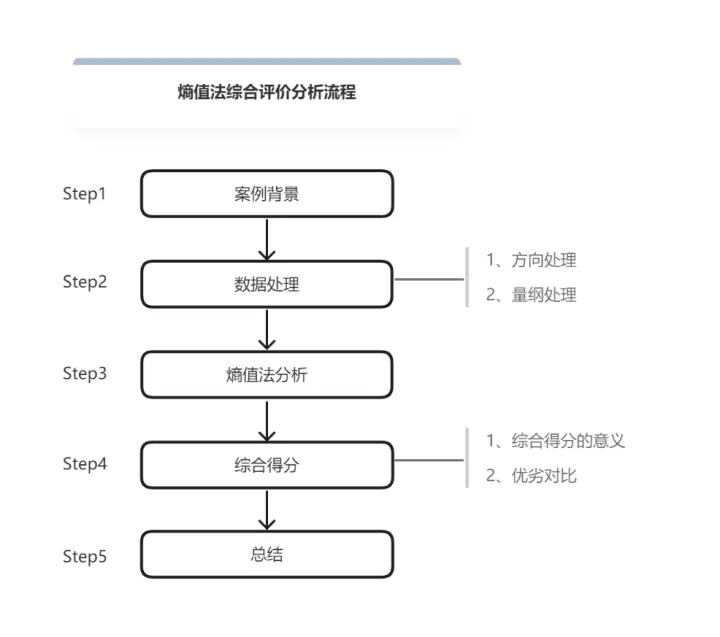
1、理想解法：有效的多指标评价方法；

2、模糊综合评判法：多指标or say多目标决策问题，解决模糊性和人的经验性；

3、数据包络分析：比较不同决策的相对有效用，多指标输入多指标输出系统；

4、灰色关联度分析：样本规律性和数量要求不高，一定程度排除决策者主管任意性，客观

5、主成分分析法：变量降维，变量解释（如果可以的话）

6、秩和比综合评价法：频数较多的评价系统，政策影响因素等级排序等相关主题

一、理想解法TOPSIS

1、原理思想

2、TOPSIS法的算法步骤

3、示例

理想解法总过程MATLAB方程：

二、模糊综合评价法

1、一级模糊综合评价在人事考核中的应用

2、多层次模糊综合评判在人事中的应用

二级模糊综合评判为MATLAB方程如下：

三、数据包络分析

1、相对有效评价问题

2、数据包络分析的编辑模型

3、编辑模型的求解——LINGO方程

4、案例2（含LINGO方程）

四、灰色关联分析法

1、灰色关联分析法具体步骤如下：

五、主成分分析法

MATLAB程序如下

六、秩和比综合评价法

1、原理

2、步骤

3、应用实例

MATLAB方程如下

七、案例分析

MATLAB程序如下：层次分析法算权重+TOPSIS

lingo程序运行结果说明：

个人学习笔记，学习教材《数学建模算法与应用》第2版综合评价章

一、理想解法

1、原理思想

设多属性决策方案集为，衡量方案优劣的属性变量为x1,x2,...,xn，这时方案集中的每个方案di(i=1,...,m)的n个属性值构成的向量是[ai1,...,ain]，它作为维空间中的一个点，能唯一地表征方案di。

正理想解是方案及D中不存在的一个最好的解，它的每个属性值都是决策矩阵中该属性的最优值；同理负理想解是虚拟的最差的解，属性值是最差值。

所以，看某个方案的优劣，就是在n维空间中将方案与正理想解和负理想解的距离进行比较，TOPSIS法中使用的是欧几里得距离，方案di与正理想解C*越近，负理想解C0越远，就说明它最优。可以据此排定方案集D中各备选方案的优先级。

要同时看正理想解C*和负理想解C0距离，是因为有时会出现两个备选方案di与正理想解的距离相同，为了区分两个方案的优劣，故引入两个方案与负理想解之间的距离，与正理想解的距离相同的方案di离负理想解较远者为优。

2、TOPSIS法的算法步骤

综合决策方法,算法

3、示例

第一步：数据预处理即属性值的规范化

属性值的类型：效益型、成本型和区间型。效益型越大越好，成本型越小越好，区间属性是某个区间最佳。

属性值规范化的三个作用：属性值有多种类型，三种属性放在同一个表中不便于直接从数值上判断方案的优劣。所以预处理后，任意属性下性能越优的方案属性值就越大；非量纲化，属性间的不可公度性不同属性量纲不同。排除量纲的影响就是非量纲化；归一化，属性值中不同指标的属性值差别很大，将数据归一化[0,1]。

常用的属性值规范化方法：

（1）线性变换

综合决策方法,算法

（2）标准0-1变换

综合决策方法,算法

（3）区间性属性值的变换

综合决策方法,算法

MATLAB公式：

clc,clear
x2 = @(qujian,lb,ub,x)(1-(qujian(1)-x)./(qujian(1)-lb)).*(x>=lb&x<qujian(1))+...
    (x>=qujian(1)&x<=qujian(2))+(1-(x-qujian(2))./(ub-qujian(2))).*...
    (x>qujian(2)&x<=ub); %定义变换的匿名函数，该语句太长，使用了两个续行符
qujian=[5,6];lb=2;ub=12; %最优区间，无法容忍下界和上界，【输入值】
x2data=[5 6 7 10 2]'; %x2属性值，【输入值】
y2 = x2(qujian,lb,ub,x2data); %调用匿名函数，进行数据交换，【输出值】

（4）向量规范化

综合决策方法,算法

（5）标准化处理

综合决策方法,算法

MATLAB程序如下：

x = [0.1 5 5000 4.7
     0.2 6 6000 5.6
     0.4 7 7000 6.7
     0.9 10 10000 2.3
     1.2 2 400 1.8]; %【输入矩阵】
y = zscore(x) %【输出】

综合决策方法,算法

第二步：权向量处理属性值

设权向量为w = [0.2, 0.3, 0.4, 0.1]，得加权得向量规范化属性矩阵表14.5。

综合决策方法,算法

第三步：求正理想解和负理想解

找计算得的最大值和最小值，但是最后一个预取毕业率要注意，不是越大越好而是越小越好。

综合决策方法,算法

第四步：计算样本（方案）与正理想解和负理想解的距离及综合指标值

各方案到正理想解的距离，负理想解的距离

综合决策方法,算法

第五步：根据指标值排序

理想解法总过程MATLAB方程：

clc,clear
a = [0.1 5 5000 4.7
    0.2 6 6000 5.6
    0.4 7 7000 6.7
    0.9 10 10000 2.3
    1.2 2 400 1.8]; % 原始数据【输入】
[m,n]=size(a);
m,n
x2 = @(qujian,lb,ub,x)(1-(qujian(1)-x)./(qujian(1)-lb)).*(x>=lb&x<qujian(1))+...
    (x>=qujian(1)&x<=qujian(2))+(1-(x-qujian(2))./(ub-qujian(2))).*...
    (x>qujian(2)&x<=ub); % 定义区间型属性值的变换，该语句太长，使用了两个续行符
qujian=[5,6];lb=2;ub=12; % 区间型属性值的最优区间、无法容忍下界和上界，【输入值】
a(:,2) = x2(qujian,lb,ub,a(:,2)); % 对区间型属性2进行区间型变换【更改区间属性2】
for j = 1:n
    b(:,j) = a(:,j)/norm(a(:,j)); % 向量规范化
end
w = [0.2 0.3 0.4 0.1]; % 各属性值的权重值【输入值】
c = b.*repmat(w,m,1); % 求加权矩阵
Cstar = max(c); % 求正理想解
Cstar(4) = min(c(:,4)) % 属性4为成本型的，所以越小越好【更改成本型属性4】
c0 = min(c); % q求负理想解
c0(4) = max(c(:,4)) % 属性4为成本型的，所以越大越好【更改成本型属性4】
for i = 1:m
    Sstar(i) = norm(c(i,:)-Cstar); % 求导正理想解的距离
    S0(i) = norm(c(i,:)-c0); % 求到负理想解的距离
end
Sstar,S0 % 显示到真理想解的距离及到负理想解的距离
f = S0./(Sstar+S0)
[sf,ind2sub] = sort(f,'descend') % 求排序结果

输出的m,n是行，列；Cstar是正理想解，c0是负理想解；Sstar到正理想解的距离，S0到负理想解的距离；f是排序指标值，sf是对指标值排序，ind2sub是对方案的排序；

二、模糊综合评价法

此方法常用于人事考核，适用情况特征如下

事件评定本身存在大量模糊性概念，这种模糊性和不确定性不是由于事件发生的条件难以控制导致的，而是由于事件本身概念不明确而引起的。这就是评定指标难以量化。如人事考核评价过程中，考核者容易受经验、人际关系等主观因素影响，对人才综合素质评价往往带有一定模糊性和经验性。

一级模糊综合评判与多级模糊综合评判主要区别如下图，一级指标和二级指标，详情请看下面2.1和2.2，重点理解例子。

综合决策方法,算法

1、一级模糊综合评价在人事考核中的应用

在指标个数较少的情况下，运用一级模糊综合评价，而在问题较复杂，指标较多的情况下，运用多层次模糊综合评价，以提高精度。

综合决策方法,算法

2、多层次模糊综合评判在人事中的应用

如果问题很复杂，指标很多的话，运用以及模糊评判没有办法有效完成任务，主要原因有两个：其一是因素过多，权数分配难以确定；其二是，即使确定了权分配，为了满足了归一化条件，每个归一化的值都会非常小，对于这种系统，可以采用多层次模糊综合评判。此处例子为二级模糊综合评判，现实中的多层次模糊综合评判可以以此类推。

综合决策方法,算法

根据最大隶属度原则，评定优或良etc

二级模糊综合评判为MATLAB方程如下：

clc,clear
% 方法一：将文件里的数字输入；方法二：定义a
a = load('mhdata.txt'); % 把表中的原始数据保持在纯文本文件mhdata.txt【输入】
% a=[0.8 0.15 0.05 0 0
% 0.2 0.6 0.1 0.1 0
% 0.5 0.4 0.1 0 0
% 0.1 0.3 0.5 0.05 0.05
% 0.3 0.5 0.1 0.05 0
% 0.2 0.2 0.4 0.1 0.1
% 0.4 0.4 0.1 0.1 0
% 0.1 0.3 0.3 0.2 0.1
% 0.3 0.2 0.2 0.2 0.1
% 0.1 0.3 0.5 0.1 0
% 0.2 0.3 0.3 0.1 0.1
% 0.2 0.3 0.35 0.15 0
% 0.1 0.3 0.4 0.1 0.1
% 0.1 0.4 0.3 0.1 0.1
% 0.3 0.4 0.2 0.1 0
% 0.1 0.4 0.3 0.1 0.1
% 0.2 0.3 0.4 0.1 0
% 0.4 0.3 0.2 0.1 0];
w = [0.4 0.3 0.2 0.1]; % 权重值【输入权重】
w1 = [0.2 0.3 0.3 0.2];
w2 = [0.3 0.2 0.1 0.2 0.2];
w3 = [0.1 0.2 0.3 0.2 0.2];
w4 = [0.3 0.2 0.2 0.3];
b(1,:) = w1*a([1:4],:); % 一级指标中的二级指标行【输入】
b(2,:) = w2*a([5:9],:); 
b(3,:) = w3*a([10:14],:);
b(4,:) = w4*a([15:end],:);
c = w*b % 【输出】

三、数据包络分析

评价多个决策单元（Decision Making Units,DMU）相对有效性的数据包络分析方法（Data Envelopment Analysis,DEA)。

是一种处理多目标决策的好方法。应用于数学规划模型计算比较决策单元之间的相对效率，对评价对象作出评价。

数据包络分析方法DEA特别适用于评价具有多输入和多输出指标系统。体现为：

（1）DEA以决策单位各输入/输出的权重为变量，从最有利于决策单元的角度进行评价，从而避免了各指标在优先意义下的权重。

（2）假定每个输入都关联到一个或多个输出，且两者确实有一定联系，使用DEA方法则不用确定这种关系的显示表达式。

DEA最突出的有点在于权重的客观性，不是根据评价者的主观认定，而是决策单元的实际数据求得的最优权重。

DEA是相对效率概率为基础，以凸分析和线性规划为工具的评价方法。DEA对社会经济系统多投入和多输出相对有效性评价，是独居优势的。

1、相对有效评价问题

输入与输出产出比的问题。例子理解。

综合决策方法,算法

2、数据包络分析的模型

DMU是决策单元。

综合决策方法,算法

14.16中目标函数，当前输出权重*输出值最大；约束条件1，指的是所有决策单元的输入权重*输入 > 输出权重*输出；约束条件2，指的是当前输入权重*输入值为1，这样目标函数就可以是输出权重*输出。

3、模型的求解——LINGO方程

求解，需要求解若干个线性规划问题，这点可以利用Lingo软件完成。

此方程主要通过14.6的式子组成。如下：综合决策方法,算法

model:
sets:
!dum,inw,outw,是集合名称;
!t是输入权重*输入，s是输出权重*输出;
dmu/1..6/:s,t,p;           !决策单元（或评价对象），p为单位坐标向量，s，t为中间变量，决策单元有6个分量【输入值】;
inw/1..2/:omega;           !输入指标权重，2为输入权重个数【输入值】;
outw/1..2/:mu;             !输出指标权重，【输入值】;

!inv,outv中的（inv,dum）表示双下标来着，x,y都为双下标的量;
inv(inw,dmu):x;            !输入变量，Xj=(x1j,x2j,x3j,...,xmj);
outv(outw,dmu):y;
endsets

data:
ctr = ?;                                   !实时输入数据，对第n个单元做评价时，就输入n。下面为输入和输出指标值;
x = 89.39 86.25 108.13 106.38 62.40 47.19  !【输入和输出】;
    64.3 99 99.6 96 96.2 79.9;
y = 25.2 28.2 29.4 26.4 27.2 25.2
    223 287 317 291 295 222;
enddata

max = @ sum(dmu(i):p(i)*t(i));             ! 当前决策单元输出权重*输出的最大值;
!确定当前决策单元是哪一个;
p(ctr) = 1; 
@ for(dmu(i)|i#ne#ctr:p(i) = 0);           ! i!=ctr时，p=0;
!定义s和t;
@ for(dmu(j):s(j) = @ sum(inw(i):omega(i)*x(i,j)); ! s = 输入权重*输入;
@for(dmu(j):t(j) = @ sum(outw(i):mu(i)*y(i,j)));   ! t = 输出权重*输出;
!14.16式子;
@for(dmu(j):s(j)>t(j)));                   ! 14.16式1：输入权重*输入>输出权重*输出;
@ sum(dmu(i):p(i)*s(i))=1;                 ! 14.16式2：当前决策单元的s = 1;
end

综合决策方法,算法

4、案例2（含LINGO方程）

综合决策方法,算法

lingo程序如下，与上面相似，就是集合和数据有差异：

model:
sets:
dmu/1..10/:s,t,p;         ! 决策单元，p为单位坐标向量，s,t为中间变量;
inw/1..3/:omega;          ! 输入权重;
outw/1..2/:mu;            ! 输出权重;
inv(inw,dmu):x;           ! 输入变量;
outv(outw,dmu):y;         ! 输出变量；
endsets

data:
ctr = ?;                  ! 实时输入数据，对第n个单元做评价时，就输入n;
x =14.4,16.9,15.53,15.4,14.17,13.33,12.83,13,13.4,14
   0.65,0.72,0.72,0.76,0.76,0.69,0.61,0.63,0.75,0.84
   31 .3,32.2,31 .87,32.23,32.4,30.77,29.23,28.2,28.8,29.1;
y =3621,3943,4086.67,4904.67,6311 .67,8173.33,10236,12094.33,13603.33,1484 1
   0,0.09,0.07,0.13,0.37,0.59,0.51,0.44,0.58,1;
enddata

max = @ sum(dmu(i):p(i)*t(i));             ! 当前决策单元输出权重*输出的最大值;
!确定当前决策单元是哪一个;
p(ctr) = 1; 
@ for(dmu(i)|i#ne#ctr:p(i) = 0);           ! i!=ctr时，p=0;
!定义s和t;
@ for(dmu(j):s(j) = @ sum(inw(i):omega(i)*x(i,j)); ! s = 输入权重*输入;
@for(dmu(j):t(j) = @ sum(outw(i):mu(i)*y(i,j)));   ! t = 输出权重*输出;
!14.16式子;
@for(dmu(j):s(j)>t(j)));                   ! 14.16式1：输入权重*输入>输出权重*输出;
@ sum(dmu(i):p(i)*s(i))=1;                 ! 14.16式2：当前决策单元的s = 1;
end

综合决策方法,算法

四、灰色关联分析法

有点类似理想解法，但是不完全一样，这里的参考数列（正理想解）由于数据处理的原因，数值全为1，整体的操作也比理想解法简单很多。

但似乎也是一种很好用的方法，优点描述如下：

将灰色关联分析法应用于供应商选择过程中，可以针对大量不确定性因素和相互关系，将定量和定性有机结合起来，是复杂的决策问题，变得简单清晰，方便计算，一定程度上排除决策者主观性，使结果客观，有一定参考性。

1、灰色关联分析法具体步骤如下：

综合决策方法,算法

（此处对上述指标的规范化处理为归一化，截取MATLAB代码如下

for i = [1 5:9] % 效益型指标标准化
a(i,:) = (a(i,:)-min(a(i,:)))/(max(a(i,:))-min(a(i,:)));
end
for i = 2:4 % 成本型指标标准化
a(i,:) = (max(a(i,:))-a(i,:))/(max(a(i,:))-min(a(i,:)));
end）

综合决策方法,算法

将灰色关联分析法应用于供应商选择过程中，可以针对大量不确定性因素和相互关系，将定量和定性有机结合起来，是复杂的决策问题，变得简单清晰，方便计算，一定程度上排除决策者主观性，使结果客观，有一定参考性。

MATLAB程序如下：

输出情况为：由于标准化的方法（方法为归一化），使参考值cankao全为1（每个指标最大值为1）；灰色关联度系数xishu；关联度guanliandu（乘以权重后）；gsort排序后的guanliandu，ind为排序后的供应商i。

clc,clear
a = [0.83 0.90 0.99 0.92 0.87 0.95
326 295 340 287 310 303
21 38 25 19 27 10
3.2 2.4 2.2 2.0 0.9 1.7
0.20 0.25 0.12 0.33 0.20 0.09
0.15 0.20 0.14 0.09 0.15 0.17
250 180 300 200 150 175
0.23 0.15 0.27 0.30 0.18 0.26
0.87 0.95 0.99 0.89 0.82 0.94];
for i = [1 5:9] % 效益型指标标准化
    a(i,:) = (a(i,:)-min(a(i,:)))/(max(a(i,:))-min(a(i,:)));
end
for i = 2:4 % 成本型指标标准化
    a(i,:) = (max(a(i,:))-a(i,:))/(max(a(i,:))-min(a(i,:)));
end
[m,n]=size(a);
cankao = max(a')' % 求参考序列的取值
t = repmat(cankao,[1,n])-a; % 求参考序列与每一个序列的差
mmin = min(min(t)); % 计算最小差
mmax = max(max(t)); % 计算最大差
rho = 0.5; % 分辨系数【输入】
xishu = (mmin+rho*mmax)./(t+rho*mmax) % 计算灰色关联系数
guanliandu = mean(xishu) % 取等权重，计算关联度，也可以乘以w【权重w输入】
[gsort,ind] = sort(guanliandu,'descend') % 对关联度从大到小排序

五、主成分分析法

综合决策方法,算法

综合决策方法,算法基于主成分分析法的步骤如下：

（1）对原始数据进行标准化处理

综合决策方法,算法

gj = zscore(gj) % 数据标准化

（2）计算相关系数矩阵R

综合决策方法,算法

r = corrcoef(gj) % 计算相关系数矩阵

（3）计算特征值和特征向量

综合决策方法,算法

% 下面利用相关系数矩阵进行主成分分析，【输出：x的列为r的特征线向量，即主成分的系数】

[x,y,z] = pcacov(r) % y为r的特征值，【输出：z为各个主成分的贡献率】

f = repmat(sign(sum(x)),size(x,1),1); % 构造与x同维数的元素为+-1的矩阵

x = x.*f; % 修改特征向量的正负号，每个特征向量乘以所有分量和的符号函数值；虽然但是实际没什么变化

（4）选择p(p<=5)个主成分，计算综合评价值

综合决策方法,算法

这里的特征根是输出的y，贡献率是z，累计贡献率是将前面的贡献率相加；

num = 3; % num为最后选取的主成分的个数【输入】

df = gj*x(:,[1:num]); % 计算各个(选择的num个数）主成分的得分

tf = df*z(1:num)/100; % 计算各年度的评价综合得分，以贡献率为的权重*num个主成分

综合决策方法,算法

这里的特征向量为输出的x，按列看！；

综合决策方法,算法

[stf,ind] = sort(tf,'descend'); % 把得分按照从高到低的次序排列

stf = stf',ind = ind' % stf是算得的综合评价值，ind是对应的原始数据的序列

MATLAB程序如下

clc,clear
gj = load('mhdata.txt');  % 把原始数据保存在纯文本文件中
% gj =[0.71 0.49 0.41 0.51 0.46
% 0.40 0.49 0.44 0.57 0.50
% 0.55 0.56 0.48 0.53 0.49
% 0.62 0.93 0.38 0.53 0.47
% 0.45 0.42 0.41 0.54 0.47
% 0.36 0.37 0.46 0.54 0.48
% 0.55 0.68 0.42 0.54 0.46
% 0.62 0.90 0.38 0.56 0.46
% 0.61 0.99 0.33 0.57 0.43
% 0.71 0.93 0.35 0.66 0.44
% 0.59 0.69 0.36 0.57 0.48
% 0.41 0.47 0.40 0.54 0.48
% 0.26 0.29 0.43 0.57 0.48
% 0.14 0.16 0.43 0.55 0.47
% 0.12 0.13 0.45 0.59 0.54
% 0.22 0.25 0.44 0.58 0.52]
gj = zscore(gj)           % 数据标准化
r = corrcoef(gj)          % 计算相关系数矩阵
% 下面利用相关系数矩阵进行主成分分析，【输出：x的列为r的特征线向量，即主成分的系数】
[x,y,z] = pcacov(r)         % y为r的特征值，【输出：z为各个主成分的贡献率】
f = repmat(sign(sum(x)),size(x,1),1);     % 构造与x同维数的元素为+-1的矩阵
x = x.*f;                 % 修改特征向量的正负号，每个特征向量乘以所有分量和的符号函数值；虽然但是实际没什么变化
num = 3;                  % num为最后选取的主成分的个数【输入】
df = gj*x(:,[1:num]);     % 计算各个(选择的num个数）主成分的得分
tf = df*z(1:num)/100;     % 计算各年度的评价综合得分，以贡献率为的权重*num个主成分
[stf,ind] = sort(tf,'descend');           % 把得分按照从高到低的次序排列
stf = stf',ind = ind'     % stf是值，ind是原始数据的序列

六、秩和比综合评价法

在医疗领域的多指标综合评价、统计预测预报、统计质量控制等方面应用广泛。秩和比是行或列秩次的平均值，是一个非参数统计量，具有0~1连续变量的特征。

1、原理

秩和比综合评价法基本原理是一个n行m列矩阵中，通过秩转换，获得无量纲统计量RSR；在此基础上，运用参数统计分析的方法与概念，研究RSR的分布；以RSR对评价对象的优劣直接排序或分档排序，从而对评价对象作出综合评价。

2、步骤

综合决策方法,算法

（1）编秩。将n个评价对象的m个评价指标排列成n*m的原始表。

综合决策方法,算法

w = aw(end,:); % 提取权重向量，最后一行为权重

a = aw([1:end-1],:); % 提取指标数据

a(:,[2,6]) = -a(:,[2,6]); % 把成本型指标转换成效益型指标，2，6列为成本型【输入】

（2）计算秩和比

综合决策方法,算法

ra = tiedrank(a) % 对每个指标值分别编秩，即对a的每一列分别编秩

[n,m] = size(ra); % 计算矩阵sa的维数

RSR = mean(ra,2)/n % 计算秩和比,mean(ra,2)每行平均值的列向量

W = repmat(w,[n,1]); % 将w拓展为[n，1]维

WRSR = sum(ra.*W,2)/n % 计算加权秩和比，sum(ra.*W,2)计算行的和

综合决策方法,算法

（3）计算概率单位

综合决策方法,算法

本次实例中各组频数都是1（因为每一年只出现了一次）；累计频数就是把之前的加起来；累计频率见公式；Probit由正态分布来：

[sWRSR,ind] = sort(WRSR); % 对加权秩和比排序

p = [1:n]/n; % 计算累计频率

p(end) = 1-1/(4*n) % 修正最后一个累计频率，最后一个累积频率按1-1(4n)估计，这个下面详讲

Probit = norminv(p,0,1)+5 % 计算标准正态分布的p分位数+5

（4）计算直线回归方程

综合决策方法,算法

X = [ones(n,1),Probit']; % 构造一元线性回归分析的数据矩阵

[ab,abint,r,rint,stats] = regress(sWRSR,X) % 一元线性回归分析

WRSRfit = ab(1)+ab(2)*Probit % 计算WRSR的估计值

综合决策方法,算法

（ 5）分档排序。按照回归方法推算的对应RSR(WRSR)估计值对评价对象进行分档排序。

3、应用实例

综合决策方法,算法

综合决策方法,算法（MATLAB的未排序输出14.19：）

综合决策方法,算法

MATLAB排序的Probit和WRSRfit输出：

综合决策方法,算法

MATLAB方程如下

clc,clear
%aw = load('mhdata.txt'); % 导入x1,...x6的数据和权重数据【输入】
aw = [75.2 3.5 38.2 370.1 101.5 10.0  % 数据和权重数据输入，权重数据在最后一行
76.1 3.3 36.7 369.6 101.0 10.3
80.4 2.7 30.5 309.7 84.8 10.0
77.8 2.7 36.3 370.1 101.4 10.2
75.9 2.3 38.9 369.4 101.2 9.61
74.3 2.4 36.7 335.3 91.9 9.2
74.6 2.2 37.5 356.2 97.6 9.3
72.1 1.8 40.3 401.7 101.1 10.0
72.8 1.9 37.1 372.8 102.1 10.0
72.1 1.5 33.2 358.1 97.8 10.4
0.093 0.418 0.132 0.100 0.098 0.159];
w = aw(end,:);           % 提取权重向量，最后一行为权重
a = aw([1:end-1],:);     % 提取指标数据
a(:,[2,6]) = -a(:,[2,6]);% 把成本型指标转换成效益型指标，2，6列为成本型【输入】
ra = tiedrank(a)         % 对每个指标值分别编秩，即对a的每一列分别编秩
[n,m] = size(ra);        % 计算矩阵sa的维数
RSR = mean(ra,2)/n       % 计算秩和比,mean(ra,2)每行平均值的列向量
W = repmat(w,[n,1]);     % 将w拓展为[n，1]维
WRSR = sum(ra.*W,2)/n    % 计算加权秩和比，sum(ra.*W,2)计算行的和
[sWRSR,ind] = sort(WRSR);% 对加权秩和比排序
p = [1:n]/n;             % 计算累计频率
p(end) = 1-1/(4*n)       % 修正最后一个累计频率，最后一个累积频率按1-1(4n)估计，不知道为啥
Probit = norminv(p,0,1)+5      % 计算标准正态分布的p分位数+5
X = [ones(n,1),Probit'];       % 构造一元线性回归分析的数据矩阵
[ab,abint,r,rint,stats] = regress(sWRSR,X)     % 一元线性回归分析
WRSRfit = ab(1)+ab(2)*Probit   % 计算WRSR的估计值
y = [1983:1992]';        % 创建的xls的序列【输入】
xlswrite('ex147.xls',[y(ind),ra(ind,:),sWRSR],1)    % 数据写入表单"Sheet1"中
xlswrite('ex147.xls',[y(ind),ones(n,1),[1:n]',p',Probit',WRSRfit',[n:-1:1]'],2)
% 数据写入表单"Sheet2"中

最后的xls表如下：

综合决策方法,算法

七、案例分析

《数学建模算法与应用》第2版 14.7.1的问题

MATLAB程序如下：层次分析法算权重+TOPSIS

clc,clear
a = load('mhdata.txt');  % 导入原始数据，并且把A,B,C,D分别替换成相应的数值
b = zscore(a); % 数据标准化
E = [1 4 2 8 2;1/4 1 1/2 2 1/2;1/2 2 1 4 1;1/8 1/2 1/4 1 1/4;1/2 2 1 4 1];
[vec,val] = eigs(E,1) % 求模最大的特征值及对应的特征向量
w = vec/sum(vec) % 求归一化特征向量，即权重
w = repmat(w',16,1) % 扩充为与数据矩阵相同的维度
c = b.*w % 计算加权属性
cstar = max(c) % 求正理想解
c0 = min(c) % 求负理想解
for i = 1:16
    sstar(i) = norm(c(i,:)-cstar);  % 求到正理想解的距离
    s0(i) = norm(c(i,:)-c0); % 求到负理想解的距离
end
f = s0./(sstar+s0);
xlswrite('book3.xls',[sstar',s0',f']) % 把计算结果写到Excel文件中，便于将来制表
[sc,ind] = sort(f,'descend')  % 求排序结果

lingo程序运行结果说明：

综合决策方法,算法

学习对象：

《数学建模算法与应用》第2版

http://t.csdn.cn/H3wSD MATLAB中mean的应用

http://t.csdn.cn/jfWpr MATLAB中repmat的应用

http://t.csdn.cn/B3U4d Lingo入门

【快速学懂Lingo软件及其编程方法】 https://www.bilibili.com/video/BV1bt411m7qD/?share_source=copy_web&vd_source=98fbab4e0ff3ef4e18cd477db479634d

【【数模常用软件Lingo教程】O奖讲解数模规划问题利器Lingo一小时速成】 https://www.bilibili.com/video/BV17T4y1K7sL/?p=2&share_source=copy_web&vd_source=98fbab4e0ff3ef4e18cd477db479634d文章来源地址https://www.toymoban.com/news/detail-555191.html

到了这里，关于综合评价与决策方法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！