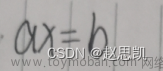将矩阵化为行最简矩阵,此时主元个数就是矩阵的秩。
例如:
矩阵
[
1
2
−
1
3
0
0
1
5
0
0
0
0
]
\begin{bmatrix} 1 & 2 & -1 & 3 \\ 0 & 0 & 1 & 5 \\ 0 & 0 & 0 & 0 \end{bmatrix}
⎣
⎡100200−110350⎦
⎤,第一行加上第二行,可得行最简矩阵形式,即
[
1
2
0
8
0
0
1
5
0
0
0
0
]
\begin{bmatrix} 1 & 2 & 0 & 8 \\ 0 & 0 & 1 & 5 \\ 0 & 0 & 0 & 0 \end{bmatrix}
⎣
⎡100200010850⎦
⎤。
此时主元(每行中最左边的第一个非零元)数为2,所以该矩阵秩为2。文章来源地址https://www.toymoban.com/news/detail-556365.html
文章来源:https://www.toymoban.com/news/detail-556365.html
到了这里,关于矩阵的秩怎么求的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!