Maple输入矩阵和向量

9月前作者：小林up 分类：Toy博客阅读(65) 违法举报

这篇具有很好参考价值的文章主要介绍了Maple输入矩阵和向量。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

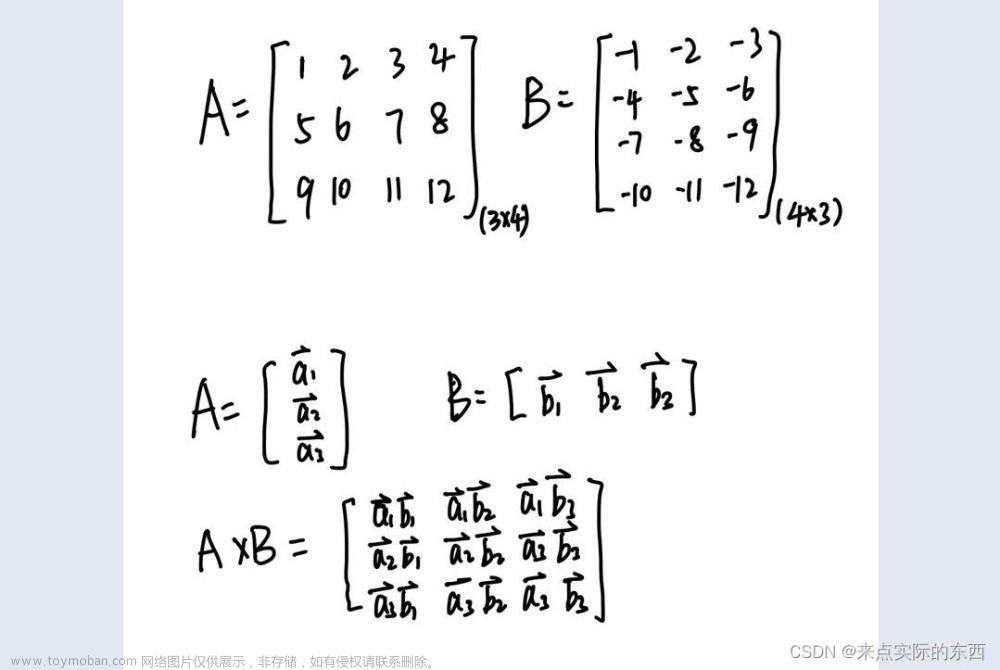
记录Maple输入矩阵的两种方式

方法1 使用LinearAlgebra报中的Matrix函数

使用LinearAlgebra报中的Matrix函数，需要使用两个中括号，有点像Python numpy的二维array。注意调用之前需要加上with(LinearAlgebra)。

with(LinearAlgebra);
A := Matrix([[0, 1, 0, -1, 5, 6], [0, 2, 0, 0, 0, -14], [2, -1, 2, -4, 0, 1], [-2, 1, -2, 2, 10, 25]]);

maple输入矩阵,Maple,矩阵,Maple

方法2 直接输入

这是我常使用的方法，感觉更加直观，比较像matlab，用分号分开每一行。

A1:=<0,1,0,-1,5,6;0,2,0,0,0,-14;2,-1,2,-4,0,1;-2,1,-2,2,10,25>;

maple输入矩阵,Maple,矩阵,Maple

可以看到两者相减是一致的，说明写的方式都是可以的。
maple输入矩阵,Maple,矩阵,Maple
Maple官方的文档附上，用逗号是列向量，用竖线是行向量。

maple输入矩阵,Maple,矩阵,Maple
更详细的，要注意行向量和列向量：

maple输入矩阵,Maple,矩阵,Maple 文章来源地址https://www.toymoban.com/news/detail-556660.html

到了这里，关于Maple输入矩阵和向量的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：

领支付宝红包赞助服务器费用

R语言矩阵、向量操作（矩阵乘法，向量内积、外积(叉乘)，矩阵转置，矩阵的逆）

创建两个四维矩阵 A 与 B，A 按列填充，B 按行填充：创建两个 n 维向量 x 和 y ：使用 t(矩阵、向量名) 即可：输出如下：使用 %*% 符号即可：输出如下：在R语言中，两个矩阵、向量的内积并不只是简单的 * 号就完事了，而是有以下两种求法：或者其结果如下： (注意区分

2024年02月12日
浏览(32)
线性代数的学习和整理6：如何表示向量/矩阵？矩阵就是向量组，矩阵的本质是什么？

目录 0 参考的知识点和目录 1 向量 1.1 向量的概念 1.2 向量如何表示 1.3 向量/矩阵的优秀表示方法：即向量空间内的有向线段 2 矩阵 2.1 矩阵就是多个列向量的集合/合并（而不是 +），矩阵就是多个列向量的一种简化书写方式？ 2.2 矩阵的加法 =等价于= 向量的加法 2.3 矩阵

2024年02月07日
浏览(52)
matlab强制转换向量或矩阵为行向量，列向量

有时候需要将向量或矩阵转为行向量，方便输出或操作，可以不用判断，利用(😃，所有元素“：”来自动获取拉平的值（注意matlab是按列优先取值）。免于判断烦恼。 a = a_row = a2 = a2_row = A1 = A1_row = A1b = A1_row = 另外提一嘴，我主要遇到的是将向量或矩阵，输出到图形中，而

2024年02月16日
浏览(45)
转置矩阵、对称矩阵、反对称矩阵以及向量的反对称矩阵

假设矩阵 A 如下表示：则其转置矩阵表示为：若矩阵 B 与其转置矩阵相等，则称矩阵 B 为对称矩阵，如：若矩阵 C 与其转置矩阵取负后相等，则称矩阵 C 为反对称矩阵，其对角线元素的值为0，如：分别定义两个向量如下：对两个向量进行叉乘得到：则向量的反对称矩阵为

2024年02月11日
浏览(60)
Cesium中常用的一些数学计算（矩阵、向量）用法——向量

刚好本人最近在研究数字孪生模拟相关的专题，涉及到三维空间中跟线代相关的计算，顺便重温了一下现代，在使用的过程中遇到的一些总结和实用技巧在下头阐述，相信这篇文章能够给短时间接触这些API的人一些启发。不同人看向量存在着差异。物理专业学生的视角，向量

2024年02月10日
浏览(36)
【考研数学】线形代数第三章——向量 | 3）向量秩的性质、向量空间、过渡矩阵

紧接前文学习完向量组秩的基本概念后，继续往后学习向量的内容。性质 1（三秩相等） —— 设 A = ( β 1 , β 2 , … , β n ) = ( α 1 , α 2 , … , α n ) T pmb{A=(beta_1,beta_2,dots,beta_n)=(alpha_1,alpha_2,dots,alpha_n)^T} A = ( β 1 , β 2 , … , β n ) = ( α 1 , α 2 , … , α n )

2024年02月11日
浏览(42)
线性代数矩阵乘法中的行向量和列向量

在矩阵中有两个概念，行向量与列向量，这是从两个不同的角度看待矩阵的组成。这篇文章将从行向量和列向量两个角度来分解矩阵的乘法。假设有两个矩阵 A 和 B 一般矩阵的乘法分解简单的理解就是A矩阵的第一行与B矩阵的第一列逐元素相乘，就是结果矩阵的左上角

2024年02月11日
浏览(45)
第四章，向量组，2-矩阵等价与向量组等价的关系

玩转线性代数(23)线性组合与线性表示的应用的笔记，相关证明以及例子见原文设有 A m ∗ n B n ∗ l = C m ∗ l A_{m*n}B_{n*l}=C_{m*l} A m ∗ n B n ∗ l = C m ∗ l ，那么A、B矩阵的行、列向量组与C的行、列向量组之间有什么关系呢？先看C的行向量组， C = A B C=AB C = A B ，根据初

2024年02月04日
浏览(43)
③matlab向量和矩阵

目录手动输入数组创建等间距向量数组创建函数手动输入数组 1.背景单个称为标量的数值实际上是一个 1×1 数组，也即它包含 1 行 1 列。任务创建一个名为 x 并且值为 4 的变量。 2.您可以使用方括号创建包含多个元素的数组。任务创建一个名为 x 的数组，其

2024年02月10日
浏览(41)
根据向量求旋转矩阵

最近在进行项目的时候需要将两个面进行旋转统一到一个面，但matlab中并没有一个合适的库函数去做这件事，于是自己开发，但网上很多对罗德里格公式的推导并不是很清晰，各关系式之间的逻辑关系之间的阐述有断层，也没有配相关的代码解析。在开始推导之前，可以先带

2024年02月07日
浏览(30)