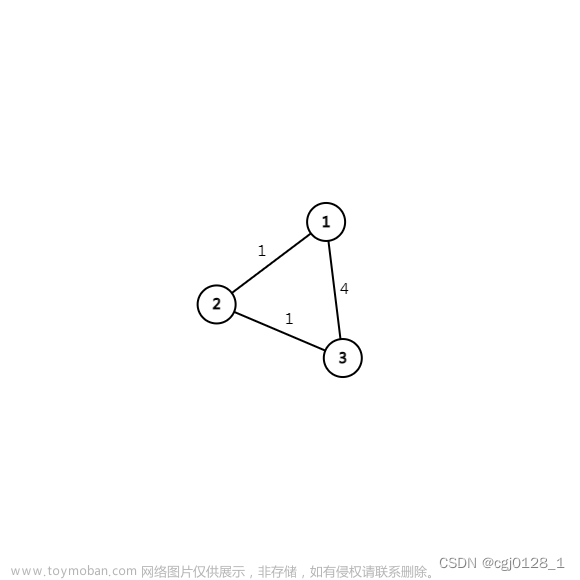
迪杰斯特拉
1.迪杰斯特拉算法: 迪杰斯特拉算法是单源最短路径问题的求解方法。单源最短路径就在给出一个固定网络,指定一个原点s,一个目标点e,求这两个点之间的最短路径。迪杰斯特拉算法用于查找图中某个顶点到其它所有顶点的最短路径,该算法既适用于无向加权图,也适用于有向加权图。
使用迪杰斯特拉算法查找最短路径时,必须保证图中所有边的权值为非负数,否则查找过程很容易出错。
2.基本原理: 从起始点出发,重复寻找当前距离起始点最近的且未访问过的结点,然后利用该结点更新距离数组,直到访问过全部结点为止,最终的距离数组即为起始点到其余个点的最短路径距离。
3.最短路径的寻找
理论依据: 由于距离数组是不断更新的,所以最终目标点索引所对应的值一定是起始点到目标点的最短路径距离。所以最后一次更新这个值的结点一定是最短路径上目标点上的一个结点(否则就会被更短的再次更新,就不可能是最后一次更新)。由于 上一个节点一定是最短路径上的结点,所以根据最优化原理,上一个结点索引所对应的值一定是起始点到该点的最短距离(否则就会出现更优路径,这条路径就不可能是最短路径)。
所以,以此反推回去,一直到起始点就可得到最短路径。
弗洛伊德
基本思想: 弗洛伊德算法定义了两个二维矩阵
1.矩阵D记录顶点间的最小路径
2.矩阵P记录顶点间最小路径中的中转点
它通过三重循环,k为中转点,v为起点,w为终点,循环比较D[v][w]和D[v][k]+D[k][w]最小值,如果D[v][k]+D[k][w]为更小值,则把D[v][k]+D[k][w]覆盖保存在D[v][w]中。
结构定义:
typedef struct struct_graph
{
char vexs[MAXN];
int vexnum;//顶点数
int edgnum;//边数
int matirx[MAXN][MAXN];//邻接矩阵
}Graph;
基本原理: 选取某个节点k作为i到j需要经过的中间节点,通过比较d(i,k)+d(k,j)和现有d(i,j)的大小,将较小值更新为路径长度,对k节点的选取进行遍历,以得到在经过所有节点时i到j的最短路径长度,通过不断加入中间点的方式更新最短路径。弗洛伊德的思想是基于动态规划。
特点: 边的权值正值负值均可,但是不可处理有负权环的情况。
弗洛伊德算法:
//(弗洛伊德算法的核心部分)
//k为中间点
for(k=0;k<G.vexnum;k++)
{
for(v=0;v<G.vexnum;v++)
{
for(w=0;w<G.vexnum;w++)
{
if(D[v][w]>(D[v][k]+D[k][w])
{
D[v][w]=D[v][k]+D[k][w];//更新最小路径
P[v][w]=P[v][k];//更新最小路径中间顶点
}
}
}
}
Bellman-Ford
1.算法介绍
Bellman-Ford算法可以解决负权图且可以判断有无负权回路(迭代超过V-1次,就说明存在负权回路)的单源最短路径问题。
优点: 可以解决有负权边的单源最短路径问题,而且可以用来判断是否有负权回路。
2.思路分析:文章来源:https://www.toymoban.com/news/detail-558202.html
1. 初始化源点s到各个点v的路径dis[v] = ∞,dis[s] = 0。
2. 进行n - 1次遍历,每次遍历对所有边进行松弛操作,满足则将权值更新。
松弛操作:以a为起点,b为终点,ab边长度为w为例。dis[a]代表源点s到a点的路径长度,dis[b]代表源点s到b点的路 径长度。如果满足下面的式子则将dis[b]更新为dis[a] + w。
dis[b] > dis[a] + w
3. 遍历都结束后,若再进行一次遍历,还能得到s到某些节点更短的路径的话,则说明存在负环路。
SPFA
1.算法思想:
队列优化,去掉一些无用的松弛操作,用队列来维护松弛造作的点。继承了Bellman-Ford算法的思想,但时间复杂度相对来说提高了很多。与BFS的算法有一些类似,利用了STL队列。
2.算法分析:文章来源地址https://www.toymoban.com/news/detail-558202.html
1.用dis数组记录点到有向图的任意一点距离,初始化起点距离为0,其余点均为INF,起点入队。
2.判断该点是否存在。(为存在就入队,标记)
3.队首出队,并将该点标记为没有访问过,方便下次入队。
4.遍历以对首为起点的有向边(t,i),如果dis[i]>dis[t]+w(t,i),则更新dis[i]。
5.如果i不在队列中,则入队标记,一直到循环结束。
到了这里,关于最短路径的求解方法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!