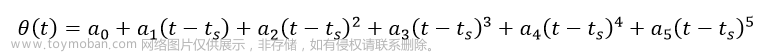运动学分类
正运动学:已知机器人各关节的变量,计算出末端执行器的位置和姿态。
逆运动学:求解一组关节变量,使机器人末端放置在特定位置并且具有期望的姿态。
运动学方法
利用矩阵建立刚体的位置和姿态,并利用矩阵建立物体的平移和旋转运动表示,研究不同构性机器人(直角坐标、球型、圆柱坐标型)的正逆运动学,最后用D-H法推导各构型机器人正逆运动学方程。
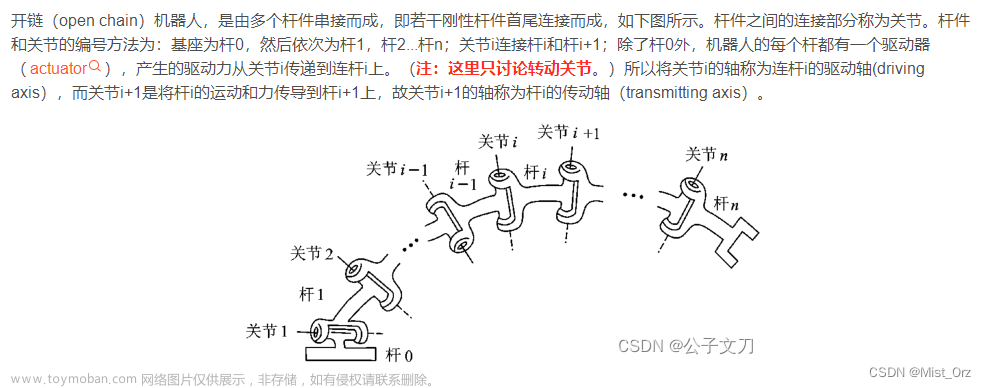
机器人机构
由于工业机器人是开环的机构,需要在机器人末端添加摄像机装置或其他辅助手段使机器人构成闭环系统。
空间向量的表示

刚体的表示

变换的表示
平移变换表示


绕轴旋转变换矩阵表示
绕x轴

绕y轴

绕z轴

复合变换表示
经过多次平移或旋转变化后,每次变换后都依次左乘齐次变换矩阵。
相对于旋转坐标系变换
经过多次平移或旋转变化后,每次变换后都依次右乘齐次变换矩阵。
变换矩阵求逆
3X3旋转矩阵的逆等于旋转矩阵的转置,这样的矩阵成为酉矩阵
4X4的其次变换矩阵求逆可分两步进行,旋转部分3X3仍为酉矩阵,直接转置处理,矩阵位置部分是向量p与向量n,o,a的点积的负值。
机器人正逆运动学推导
分别分析机器人的位置和姿态的正逆运动学,再将其结合在一起形成方案。
位置的正逆运动学
笛卡尔坐标系
笛卡尔坐标系只能沿着x,y,z三个坐标轴进行平移运动,机器人手定位通过分别沿s三个轴的平移组成。
正运动学是简单地平移矩阵,逆运动学只需设置期望位置等于P。
圆柱坐标系
圆柱坐标系包含有两个线性平移以及一个旋转运动,其顺序是:沿着x轴移动r,绕z轴转α度,再沿z轴移动l,变换都是相对于参考坐标轴,依次左乘变换矩阵得
球坐标系
球坐标系包含有一个线性平移和两个旋转运动,其顺序是:沿着z轴移动r,绕y轴转β,再绕z轴转γ,依次左乘变换矩阵得
姿态的正逆运动学
在不改变位置的前提下,适当旋转坐标系使其达到期望姿态
三种常见构型:
a.滚动、俯仰、偏航角(RPY)
b.欧拉角
c.链式关节
滚动、俯仰、偏航角(RPY)
表示RPY姿态变换矩阵
假设RPY所得最终姿态用向量n,o,a表示,则逆运动学解为


欧拉角
表示欧拉角转换矩阵为
假设欧拉角所得最终姿态用向量n,o,a表示,则逆运动学解为
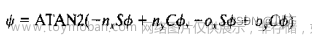

位姿正逆运动学方程
表示机器人最终位姿的矩阵是位置矩阵和姿态矩阵的组合,该矩阵取决于所用的坐标系
假设机器人运动由直角坐标和RPY组合而成,该矩阵为
假设机器人运动由求坐标定位、欧拉角定姿态,这里位置由球坐标决定,姿态由球坐标和欧拉角决定,该矩阵为
机器人正运动学D-H表示法

从参考坐标自开始,将其转换到机器人基座,然后到第一个关节、第二个关节,直至末端执行器。

为简化矩阵A的计算,可制作一张关节和连杆参数的表格,其中每个连杆和关节数值均可从机器人原理图确定,并将参数代入A矩阵。此表格成为D-H参数表。
机器人逆运动学求解
将RHS矩阵依次左乘各关节变换矩阵的逆进行解耦运算,得到所有关节的反解公式,必须根据机器人构型,做好数学处理得到逆解公式,最后仅需为计算机编程计算最终解。文章来源:https://www.toymoban.com/news/detail-558715.html
D-H表示法的缺陷
D-H表示法仅适用于每个关节有两个自由度的机器人情况。文章来源地址https://www.toymoban.com/news/detail-558715.html
到了这里,关于机器人位置运动学的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!