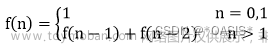递归相关知识2-Toy模板网

这篇具有很好参考价值的文章主要介绍了递归相关知识2。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

递归相关知识2

多路递归--斐波那契额数列

import java.util.Arrays;

//递归求斐波那契第n项
public class feibonaqie {
    public static int fibonacci(int n){
        int []cache=new int[n+1];
        Arrays.fill(cache,-1);
        cache[0]=0;
        cache[1]=1;//[0,1,-1,-1,-1,-1]
        return f(n,cache);
    }

    public static int f(int n,int[]cache){
     /*   if(n==0){
            return 0;
        }
        if(n==1){
            return 1;
        }*/
        if(cache[n]!=-1){
            return cache[n];
        }
        int x=f(n-1,cache);
        int y=f(n-2,cache);
        cache[n]=x+y;
        return cache[n];
    }

    /*public static void main(String[] args) {
        int f=f(8);
        System.out.println(f);
    }*/
}

汉诺塔问题

import java.util.LinkedList;

public class hannuota {
    static LinkedList<Integer> a=new LinkedList<>();//三根柱子
    static LinkedList<Integer> b=new LinkedList<>();
    static LinkedList<Integer> c=new LinkedList<>();

    //3 2 1

    static void init(int n){
        for(int i=n;i>=1;i--){
            a.addLast(i);
        }
    }
     /*
     Params:n-圆席个数
a-源
b-信
c-目
      */

    static void move(int n,LinkedList<Integer> a,LinkedList<Integer> b,
                     LinkedList<Integer> c){
        if(n==0){
            return;
        }
       move(n-1,a,c,b);
        c.addLast(a.removeLast());//中间
        print();
        move(n-1,b,a,c);
    }
    public static void main(String[]args){
        init(3);
      /*  System.out.println(a);
        System.out.println(b);
        System.out.println(c);
        b.addLast(a.removeLast());*/
        print();
        move(3,a,b,c);
    }




    private static void print() {
        System.out.println("----------------------");
        System.out.println(a);
        System.out.println(b);
        System.out.println(c);
    }
}

爆栈问题

//递归求和n+n-1+...+1
public class baozhan {
    //f(n)=f(n-2)+n;


    public static long sum(long n){
     if(n==1){
         return 1;
     }
     return sum(n-1)+n;
    }

    public static void main(String[] args) {
       /* System.out.println(sum(15000));*///爆栈
    }
}

杨辉三角

第一种,时间复杂度最高,空间复杂度最高

public class yanghuisanjiao {

    private static int element(int i,int j){
        if(j==0||i==j){
            return 1;
        }
        return element(i-1,j-1)+element(i-1,j);
    }
 private static void printSpace(int n,int i){
        int num=(n-1-i)*2;
     for (int j = 0; j < num; j++) {
         System.out.print(" ");
     }
 }
    public static void print(int n){
        for (int i = 0; i < n; i++) {
            printSpace(n,i);
            for (int j = 0; j <= i; j++) {
                System.out.printf("%-4d",element(i,j));
            }
            System.out.println();
        }
    }
    public static void main(String[] args) {
      /*  System.out.println(element(4,2));*/
        print(5);
    }
}

第二种--时间复杂度降低,空间复杂度提升

public class yanghuisanjiao1 {
/*
优化1·使用二组数组记忆法
Params:triangle-二维数组
i-行坐标
j-列坐标
Returns:该坐标元素值
 */
    private static int element1(int[][]triangle,int i,int j){
        if(triangle[i][j]>0){
            return triangle[i][j];
        }
        if(j==0||i==j){
            triangle[i][j]=1;
            return 1;
        }
        triangle[i][j]=element1(triangle,i-1,j-1)+element1(triangle,i-1,j);
        return triangle[i][j];
    }
 private static void printSpace(int n,int i){
        int num=(n-1-i)*2;
     for (int j = 0; j < num; j++) {
         System.out.print(" ");
     }
 }
    public static void print(int n){
        int[][]triangle=new int[n][];
        for (int i = 0; i < n; i++) {//行
            triangle[i]=new int[i+1];
         /*   printSpace(n,i);*/
            for (int j = 0; j <= i; j++) {
                System.out.printf("%-4d",element1(triangle,i,j));
            }
            System.out.println();
        }
    }
    public static void main(String[] args) {
      /*  System.out.println(element(4,2));*/
        print(5);
    }
}

时间复杂度,空间复杂度同时提升

public class yanghuisanjiao2 {
/*
优化2·使用二组数组记忆法
Params:triangle-二维数组
i-行坐标
j-列坐标
Returns:该坐标元素值
 */


    //动态规划--注意：还可以透过每一行的前一项计算半下一项，不必借助上一行，这与杨辉三角的另一个特性有关，
 /*   private static int element1(int[][]triangle,int i,int j){
        if(triangle[i][j]>0){
            return triangle[i][j];
        }
        if(j==0||i==j){
            triangle[i][j]=1;
            return 1;
        }
        triangle[i][j]=element1(triangle,i-1,j-1)+element1(triangle,i-1,j);
        return triangle[i][j];
    }
 private static void printSpace(int n,int i){
        int num=(n-1-i)*2;
     for (int j = 0; j < num; j++) {
         System.out.print(" ");
     }
 }*/
    public static void print2(int n){
       int[]row=new int[n];
        for (int i = 0; i < n; i++) {//行
      /*      triangle[i]=new int[i+1];*/
         /*   printSpace(n,i);*/
            createRow(row,i);
            for (int j = 0; j <= i; j++) {
                System.out.printf("%-4d",row[j]);
            }
            System.out.println();
        }
    }
    private static void createRow(int[]row,int i){
        if(i==0){
            row[0]=1;
            return;
        }
        for (int j = i; j >0 ; j--) {
            row[j]=row[j]+row[j-1];
        }
    }

    public static void main(String[] args) {
      /*  System.out.println(element(4,2));*/
        print2(5);
    }
}

数据结构素数实现

class FuShu{
    int real; //实部real、虚部image；
    int image;
    FuShu(int real, int image) { //构造方法：赋初值；
        this.real = real;
        this.image = image;
    }

    FuShu add(FuShu s1) { // 加法运算 FuShu add(FuShu s1)；
        FuShu tmp = new FuShu(real + s1.real, image + s1.image);
        return tmp;
    }
}

public class xubu {
    public static void main(String[] args) { //两个复数相加，输出结果
        FuShu s1 = new FuShu(1, 2);
        FuShu s2 = new FuShu(2, 3);
        FuShu s3 = s2.add(s1);
        System.out.println(s3.real + " + " + s3.image + "i");
    }

}

文章来源地址https://www.toymoban.com/news/detail-560595.html

到了这里，关于递归相关知识2的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！