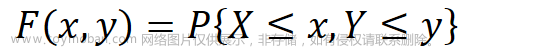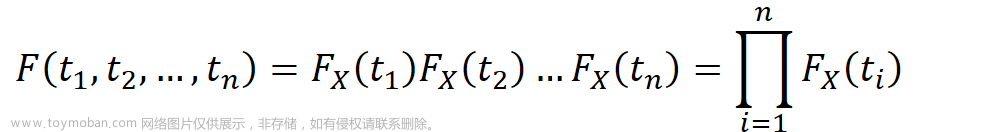目录
1 问题：
2 结论
3 实验1
4 实验2
5 实验3
6 实验4
5 各种规律总结
5.1 1
5.2 2
5.3 3
5.4 4
6 超几何分布，二项分布，泊松分布，三者用EXCEL模拟
6.1 简单的扩展到泊松分布
6.2 比较整体的动态过程，增加实验次数时
1 问题：
- 从一个简单模型说开去
- 比如，有10个球，其中有x个A，y个B，其中x+y=10
- 现在要知道连抽4次其中有2次为A的概率（放回）, 这个是二项分布
- 现在要知道连抽4次其中有2次为A的概率（不放回），这个是超几何分布
- 这两者计算结果一样吗？大概率会不一样
- 但是不一样的点在哪儿？
2 结论
- 在这个试验里
- 由于A球的概率p 永远== A球数/ 总样本数 == 超几何分布的M/N
- 所以二项分布的期望 E(X)=np == E(X)=n*M/P
- 这个我觉得是特例，能给我们什么思考呢？
- 虽然期望相同
- 但是取不同的k值，即要求抽出A球的个数不同时
- 放回--对应的二项分布，和不放回对应的--超几何分布，概率是不一样的，概率分布函数差异可能还很大。
- 方差也不同
- 超几何分布，当N越大，也就是M/N越小的时候，越趋向于二项分布，因为不放回对总体样本量的影响变得很小了。
- 但是事实上当N越大，M也很大，也就是M/N越大的时候，超几何分布也趋向于二项分布！
- 其实是要求 样本n/N 很小，k也相对N很小时，超几何分布趋向于二项分布
- 所以，需要注意，小样本数量的时候，二项分布和超几何分布的概率差异很大！！
- 但是当N变大，同时M/N越小，二项分布和超几何分布的pdf图形就很重合了！
3 实验1
- 比如，有10个球，其中有2个A，8个B，其中x+y=10
- 抽奖4次，然后需要求连抽2次都是A求的概率
- 现在要知道连抽4次其中有2次为A的概率（放回），见图中二项分布的计算
- 现在要知道连抽4次其中有2次为A的概率（不放回），见图中超几何分布的计算
4 实验2
- 比如，有10个球，其中有4个A，6个B，其中x+y=10
- 抽奖2次，然后需要求连抽2次都是A求的概率
- 现在要知道连抽2次其中有2次为A的概率（放回），见图中二项分布的计算
- 现在要知道连抽2次其中有2次为A的概率（不放回），见图中超几何分布的计算
5 实验3
- 比如，有30个球，其中有5个A，25个B，其中x+y=30
- 抽奖10次，然后需要求连抽5次都是A求的概率
- 现在要知道连抽10次其中有5次为A的概率（放回），见图中二项分布的计算
- 现在要知道连抽10次其中有5次为A的概率（不放回），见图中超几何分布的计算
6 实验4
- 比如，有100个球，其中有5个A，95个B，其中x+y=30
- 其实是要求 样本n/N 很小，k也相对N很小时，超几何分布趋向于二项分布
- 极大扩大了N，其实是为了让 M/N 变小很多
- 抽奖10次，然后需要求连抽5次都是A求的概率
- 现在要知道连抽10次其中有5次为A的概率（放回），见图中二项分布的计算
- 现在要知道连抽10次其中有5次为A的概率（不放回），见图中超几何分布的计算
极大扩大了N，但同时让M也变大
N=100,M=95, m/n很大，图形也是基本重合的
其实是为了让 M/N 变小很多
5 各种规律总结
5.1 1
5.2 2
5.3 3
5.4 4
6 超几何分布，二项分布，泊松分布，三者用EXCEL模拟
6.1 简单的扩展到泊松分布
1 M，N都趋向∞时，超几何分布趋向二项分布
2 n足够大，np固定，二项分布概率收敛于泊松分布，
近似成立的前提要求n足够大，而p足够小，np不是很小
3 他们的期望都是一样的，概率分布pdf不同
4 其中超几何分布3个参数，二项分布2个参数，泊松分布1个参数
M/N 趋向于P，而np=λ
画图注意
为了看出明显差别，只取前5个数据做曲线比较即可
文章来源地址https://www.toymoban.com/news/detail-560882.html
6.2 比较整体的动态过程，增加实验次数时
- 把数据总量S扩展到30条，
- 手动修改实验次数可以发现动态规律
- 那就是二项分布的PDF图形在趋向于 泊松分布
文章来源：https://www.toymoban.com/news/detail-560882.html
到了这里，关于概率论的学习和整理15： 超几何分布，二项分布，泊松分布是如何趋近收敛的?的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
