简单知识导入:
DES算法是属于对称密码算法中的分组加算法。
分组加密和流密码加密是相对应的。
流密码是逐字节进行加密,即一个字节一个字节进行加密
分组加密算法也叫块加密,将明文分成固定字节块,对每个字节块分别进行加密,最后拼接在一起得到密文
密钥长64位,56位参与运算,其余8位为校验位。(8,16,24,32,40,48,56,64) 可以看出是8的倍数
当n个64位明文数据块都经过DES加密处理后,所得到的n个64位密文数据块串在一起就是密文。
具体过程:
采用
F
e
i
s
t
e
l
算法
:
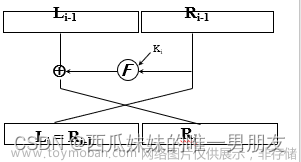
采用Feistel算法:
采用Feistel算法:
L
i
=
R
i
−
1
L_i = R_{i-1}
Li=Ri−1
R
i
=
L
i
−
1
⊕
f
(
R
i
−
1
,
K
i
)
R_i = L_{i-1} \oplus f(R_{i-1}, K_i)
Ri=Li−1⊕f(Ri−1,Ki)

首先对 64 b i t s 的明文进行初始 I P 置换,得到打乱顺序的 64 b i t s 的数据 接着对它对半分,得到 32 b i t s 的 L 0 和 R 0 自此开始进入 F e i s t e l 算法,知道 R 就很容易知道 L , 所以要解决就得从 R 入手, 已知 R i = L i − 1 ⊕ f ( R i − 1 , K i ) , f ( ) 即使图中的 F 轮函数,进行完【 4. P 置换】后即可得到 f ( R i − 1 , K i ) 接着将其与 L i − 1 进行异或即可得到 R i , 自此第一轮运算结束, 经过 16 轮相同的运算得到 L 16 和 R 16 , 拼接在一起后进行最后的逆初始置换即可得到最终的密文 首先对64bits的明文进行初始IP置换,得到打乱顺序的64bits的数据\\接着对它对半分,得到32bits的L_{0}和R_{0}\\自此开始进入Feistel算法,知道R就很容易知道L,所以要解决就得从R入手,\\ 已知R_i = L_{i-1} \oplus f(R_{i-1}, K_i),\\f()即使图中的F轮函数,进行完【4.P置换】后即可得到f(R_{i-1}, K_i)\\ 接着将其与L_{i-1}进行异或即可得到R_{i},自此第一轮运算结束,\\经过16轮相同的运算得到L_{16}和R_{16},\\拼接在一起后进行最后的逆初始置换即可得到最终的密文 首先对64bits的明文进行初始IP置换,得到打乱顺序的64bits的数据接着对它对半分,得到32bits的L0和R0自此开始进入Feistel算法,知道R就很容易知道L,所以要解决就得从R入手,已知Ri=Li−1⊕f(Ri−1,Ki),f()即使图中的F轮函数,进行完【4.P置换】后即可得到f(Ri−1,Ki)接着将其与Li−1进行异或即可得到Ri,自此第一轮运算结束,经过16轮相同的运算得到L16和R16,拼接在一起后进行最后的逆初始置换即可得到最终的密文
下面我们对照图中一个一个来讲解
IP置换( 64 − > 64 64->64 64−>64)
按照一定的规则,将原来的
64
比特的二进制数进行重新排序,
这里的规则即指初始置换表(最后的
I
P
逆置换和此处置换过程一模一样,仅表不同),
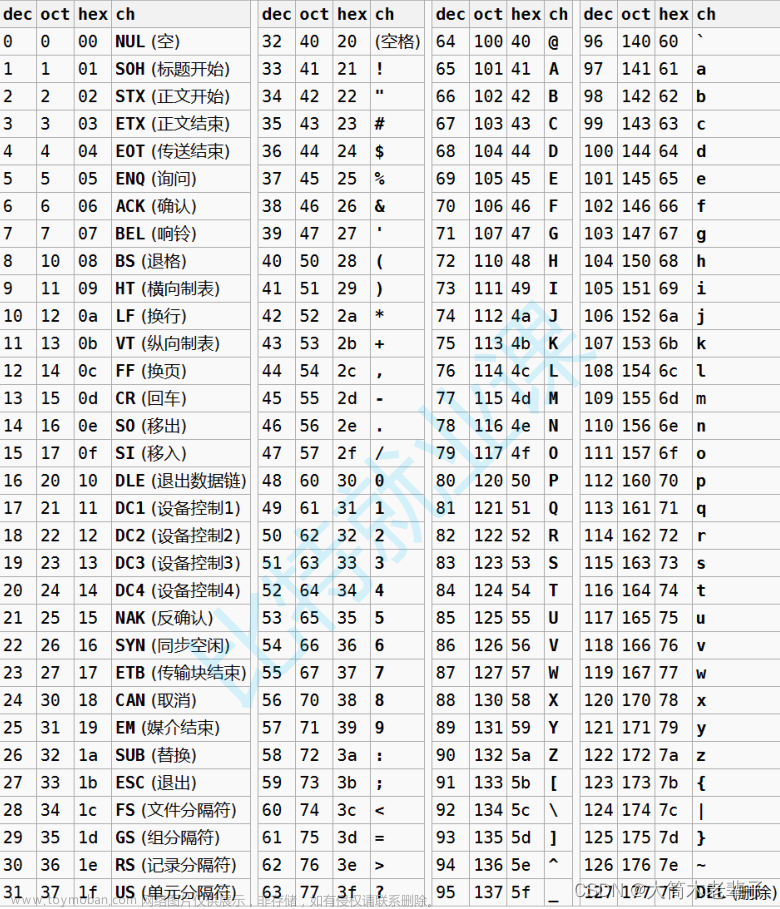
对照下面的表,将二进制明文的第
58
位放到第一位,
第
50
位放到第二位,以此类推,最终得到重新排序的数据。自此,
I
P
置换完成。
按照一定的规则,将原来的64比特的二进制数进行重新排序,\\这里的规则即指初始置换表(最后的IP逆置换和此处置换过程一模一样,仅表不同),\\ 对照下面的表,将二进制明文的第58位放到第一位,\\第50位放到第二位,以此类推,最终得到重新排序的数据。自此,IP置换完成。
按照一定的规则,将原来的64比特的二进制数进行重新排序,这里的规则即指初始置换表(最后的IP逆置换和此处置换过程一模一样,仅表不同),对照下面的表,将二进制明文的第58位放到第一位,第50位放到第二位,以此类推,最终得到重新排序的数据。自此,IP置换完成。
轮函数–E扩展置换( 32 − > 48 32->48 32−>48)
我觉得这里对照下面的图看是能看懂的,先将
32
b
i
t
s
的
R
分成
8
组,每组
4
b
i
t
s
,
每组最前和最后各加
1
b
i
t
s
,
不是随便加,按图中所给的表进行扩展
我觉得这里对照下面的图看是能看懂的,先将32bits的R分成8组,每组4bits,\\每组最前和最后各加1bits,不是随便加,按图中所给的表进行扩展
我觉得这里对照下面的图看是能看懂的,先将32bits的R分成8组,每组4bits,每组最前和最后各加1bits,不是随便加,按图中所给的表进行扩展
不好理解的话举个例子:①中是
32
b
i
t
s
的数据,按照置换表进行置换后得到③④
(此过程和最开始的
I
P
置换的原理和过程是一样的)
扩展后得到
48
b
i
t
s
不好理解的话举个例子:①中是32bits的数据,按照置换表进行置换后得到③④\\(此过程和最开始的IP置换的原理和过程是一样的)\\扩展后得到48bits
不好理解的话举个例子:①中是32bits的数据,按照置换表进行置换后得到③④(此过程和最开始的IP置换的原理和过程是一样的)扩展后得到48bits
轮函数–与子密钥异或( 48 − > 48 48->48 48−>48)
上一步得到的拓展流与子密钥异或 , 子密钥均为 48 b i t s ( 为什么是 48 b i t s ,文章最后来讲 ) 上一步得到的拓展流与子密钥异或,子密钥均为48bits\\(为什么是48bits,文章最后来讲) 上一步得到的拓展流与子密钥异或,子密钥均为48bits(为什么是48bits,文章最后来讲)
轮函数–S盒压缩处理( 48 − > 32 48->32 48−>32)
首先先将
48
b
i
t
s
输入等分为
8
块,每块
6
b
i
t
s
,
压缩后得到
4
位的输出,最终得到
32
b
i
t
s
输出,那如何进行压缩呢?(请移步下图的举例)
首先先将48bits输入等分为8块,每块6bits,\\压缩后得到4位的输出,最终得到32bits输出,那如何进行压缩呢?(请移步下图的举例)
首先先将48bits输入等分为8块,每块6bits,压缩后得到4位的输出,最终得到32bits输出,那如何进行压缩呢?(请移步下图的举例)

举个例子:
例如前
6
位
111111
,取头尾两个结合得到二进制
11
,转为
10
进制
3
,将其作为行数
中间四位数据组合得到二进制
1111
,转为
10
进制
15
,将其作为列数,
到
S
盒中相应的行列中去找,得到
13
,
13
转成的二进制数
1101
即为最终结果
自此,
6
b
i
t
s
−
>
4
b
i
t
s
,
48
b
i
t
s
−
>
32
b
i
t
s
举个例子:\\例如前6位111111,取头尾两个结合得到二进制11,转为10进制3,将其作为行数\\中间四位数据组合得到二进制1111,转为10进制15,将其作为列数,\\到S盒中相应的行列中去找,得到13,13转成的二进制数1101即为最终结果\\自此,6bits->4bits,48bits->32bits
举个例子:例如前6位111111,取头尾两个结合得到二进制11,转为10进制3,将其作为行数中间四位数据组合得到二进制1111,转为10进制15,将其作为列数,到S盒中相应的行列中去找,得到13,13转成的二进制数1101即为最终结果自此,6bits−>4bits,48bits−>32bits
注意:行列都是从0开始,故等下代码阶段在S盒中找数,行列不需减一

轮函数–P盒置换
S
盒所得结果再经过
P
盒置换(与初始
I
P
置换过程相同)。
至此,一次轮函数操作完毕
S盒所得结果再经过P盒置换(与初始IP置换过程相同)。\\至此,一次轮函数操作完毕
S盒所得结果再经过P盒置换(与初始IP置换过程相同)。至此,一次轮函数操作完毕
异或
一次轮函数加密后的数据与 L i − 1 进行异或即可得到 R i ( R i = L i − 1 ⊕ f ( R i − 1 , K i ) ) 自此,一轮迭代完成 一次轮函数加密后的数据与L_{i-1}进行异或即可得到R_{i}(R_i = L_{i-1} \oplus f(R_{i-1}, K_i))\\自此,一轮迭代完成 一次轮函数加密后的数据与Li−1进行异或即可得到Ri(Ri=Li−1⊕f(Ri−1,Ki))自此,一轮迭代完成
IP逆置换
进行 16 轮相同的运算,得到 L 16 , R 16 后将其进行拼接得到 64 b i t s 的数据, 将该 64 b i t s 的数据进行 I P 逆置换后即可得到最终密文 进行16轮相同的运算,得到L_{16},R_{16}后将其进行拼接得到64bits的数据,\\将该64bits的数据进行IP逆置换后即可得到最终密文 进行16轮相同的运算,得到L16,R16后将其进行拼接得到64bits的数据,将该64bits的数据进行IP逆置换后即可得到最终密文
注意:以上所有置换表都是已知的,固定的,给定的,不可改的(但如果有人拿此出题进行修改就不好说了)
接下来讲讲密钥生成
密钥生成
64
b
i
t
s
密钥(种子密钥),首先通过
P
C
−
1
表的置换得到
56
b
i
t
s
数据
(里面无
8
的倍数,故该表的主要作用是去除校验码)
平分分别得到
28
b
i
t
s
的
C
0
,
D
0
根据移位次数表将
C
,
D
进行左移
第一次:将
C
0
,
D
0
左移
1
位得到
C
1
,
D
1
将
C
1
,
D
1
进行拼接再通过
P
C
−
2
表置换得到第一轮子密钥
K
1
第二次:将
C
1
,
D
1
左移
1
位得到
C
2
,
D
2
将
C
2
,
D
2
进行拼接再通过
P
C
−
2
表置换得到第一轮子密钥
K
2
第三次:将
C
2
,
D
2
左移
2
位得到
C
3
,
D
3
将
C
3
,
D
3
进行拼接再通过
P
C
−
2
表置换得到第一轮子密钥
K
3
以此类推,最终生成
16
轮子密钥
64bits密钥(种子密钥),首先通过PC-1表的置换得到56bits数据\\(里面无8的倍数,故该表的主要作用是去除校验码)\\平分分别得到28bits的C_{0},D_{0}\\根据移位次数表将C,D进行左移\\ 第一次:将C_{0},D_{0}左移1位得到C_{1},D_{1}\\ \hspace{4em}将C_{1},D_{1}进行拼接再通过PC-2表置换得到第一轮子密钥K_{1}\\ 第二次:将C_{1},D_{1}左移1位得到C_{2},D_{2}\\ \hspace{4em}将C_{2},D_{2}进行拼接再通过PC-2表置换得到第一轮子密钥K_{2} \\ 第三次:将C_{2},D_{2}左移2位得到C_{3},D_{3}\\ \hspace{4em}将C_{3},D_{3}进行拼接再通过PC-2表置换得到第一轮子密钥K_{3}\\ 以此类推,最终生成16轮子密钥
64bits密钥(种子密钥),首先通过PC−1表的置换得到56bits数据(里面无8的倍数,故该表的主要作用是去除校验码)平分分别得到28bits的C0,D0根据移位次数表将C,D进行左移第一次:将C0,D0左移1位得到C1,D1将C1,D1进行拼接再通过PC−2表置换得到第一轮子密钥K1第二次:将C1,D1左移1位得到C2,D2将C2,D2进行拼接再通过PC−2表置换得到第一轮子密钥K2第三次:将C2,D2左移2位得到C3,D3将C3,D3进行拼接再通过PC−2表置换得到第一轮子密钥K3以此类推,最终生成16轮子密钥
注:经过PC-2,得到48位子密钥(56 --> 48)(9,18,22,25,35,38,43,54 not in PC-2)

代码部分
# 本脚本名: __table.py
# 明文M 的初始置换 IP
IP = [58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6,
64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7] # 将明文中的第58位换到第一位
# 逆初始置换 IP^-1
IP_INV = [40, 8, 48, 16, 56, 24, 64, 32,
39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25]
# 右子密钥扩展表 32->48位
E = [32, 1, 2, 3, 4, 5,
4, 5, 6, 7, 8, 9,
8, 9, 10, 11, 12, 13,
12, 13, 14, 15, 16, 17,
16, 17, 18, 19, 20, 21,
20, 21, 22, 23, 24, 25,
24, 25, 26, 27, 28, 29,
28, 29, 30, 31, 32, 1]
# 轮结构中的F函数中的置换P
P = [16, 7, 20, 21,
29, 12, 28, 17,
1, 15, 23, 26,
5, 18, 31, 10,
2, 8, 24, 14,
32, 27, 3, 9,
19, 13, 30, 6,
22, 11, 4, 25]
# 压缩置换: 64位母密钥->56位母密钥
PC_1 = [57, 49, 41, 33, 25, 17, 9,
1, 58, 50, 42, 34, 26, 18,
10, 2, 59, 51, 43, 35, 27,
19, 11, 3, 60, 52, 44, 36,
63, 55, 47, 39, 31, 23, 15,
7, 62, 54, 46, 38, 30, 22,
14, 6, 61, 53, 45, 37, 29,
21, 13, 5, 28, 20, 12, 4]
# 压缩置换: 56位左右密钥->48位子密钥
PC_2 = [14, 17, 11, 24, 1, 5,
3, 28, 15, 6, 21, 10,
23, 19, 12, 4, 26, 8,
16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55,
30, 40, 51, 45, 33, 48,
44, 49, 39, 56, 34, 53,
46, 42, 50, 36, 29, 32]
# 左右子密钥的循环移位表
ROTATE = [1, 1, 2, 2, 2, 2, 2, 2,
1, 2, 2, 2, 2, 2, 2, 1]
# 8 个 S 盒
SBOX = [
[14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7,
0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8,
4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0,
15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13],
[15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10,
3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5,
0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15,
13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9],
[10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8,
13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1,
13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7,
1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12],
[7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15,
13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9,
10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4,
3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14],
[2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9,
14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6,
4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14,
11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3],
[12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11,
10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8,
9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6,
4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13],
[4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1,
13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6,
1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2,
6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12],
[13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7,
1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2,
7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8,
2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11]]
# 本脚本名: __util.py
from __table import *
import time
def permutate(bitstr, table):
""" 通用置换运算
@table: 置换盒
"""
res = ""
for i in table:
res += bitstr[i-1] # 下标从0开始,故减一
return res
def leftShift(key, num):
""" 子密钥LR: 左循环移位
@key: 待移位的子密钥
@num: 列表左移位位数
"""
return key[num:] + key[0:num]
def XOR(str1, str2):
""" 两比特串进行异或 """
res = ""
for i in range(0, len(str1)):
xor = int(str1[i]) ^ int(str2[i])
res += str(xor)
return res
def Sbox(binstr):
""" S盒置换: 48位->32位 """
box = 0 # S盒的索引
res = ""
for i in range(0, len(binstr), 6):
tmp = binstr[i:i+6]
row = int(tmp[0] + tmp[5], 2) # 头尾数据结合成的2进制数据转化为10进制作为行数
col = int(tmp[1:5], 2) # 中间4位数据结合成的2进制数据转换为10进制作为列数
num = bin(SBOX[box][16*row+col])[2:].zfill(4) # 0是包含在里面的,所以不需要row-1,都是从0开始的。然后将在s盒中查到的数值转化为4位的2进制数
# zfill(4) 不足4位左侧填充0以补全4位
# 这样将48位分成8 * 6 ,然后6->4,最后得到8 * 4 = 32比特的数据
res += num
box += 1
return res
def createSubKey(key64):
""" 64位母密钥->16轮的48位子密钥列表
@key64: 输入的64位加密密钥
@return: 16轮子密钥列表
"""
subkey = []
key56 = permutate(key64, PC_1) # 64位密钥压缩置换,64bits变58bits(将校验位去除)
C28b, D28b = key56[0:28], key56[28:] # 56位密钥左右平分
for i in range(16):
C28b = leftShift(C28b, ROTATE[i]) # 左循环移位
D28b = leftShift(D28b, ROTATE[i]) # 左循环移位
subkey.append(permutate(C28b + D28b, PC_2)) # 得到一轮子密钥,加到子密钥subkey列表中去
return subkey
def turnFunction(R32b, subkey):
""" 轮结构中的F函数
@R32b: F函数输入参数 32位的右明文
@subkey: F函数输入参数 48位子密钥
"""
R48b = permutate(R32b, E) # E盒扩展: 右明文32位->48位
# E扩展置换,将32位输入扩展为48位输出(要与48比特的密钥进行运算(密钥中58位参与运算,但如何到48比特,密钥生成过程中会讲,如今已知的是K1到K16都是48比特的子密钥))
R48b = XOR(R48b, subkey) # 两异或: 扩展流与子密钥异或 R_(i-1) ^ K_i
R32b = Sbox(R48b) # S盒压缩: 压缩48位->32位
Fout = permutate(R32b, P) # P盒置换
return Fout # 至此,一次轮函数操作完毕
def hexToBit(hexstr):
""" 十六进制字符串->二进制比特流(每字符4位) """
binstr = ""
for i in hexstr:
binstr += bin(int(i,16))[2:].zfill(4)
return binstr
def bitToHex(bitstr):
""" 二进制比特流->十六进制字符串 """
hexstr = ""
for i in range(0, len(bitstr), 4):
hexstr += hex(int(bitstr[i:i+4], 2))[2:].upper()
return hexstr
def takeTime(func):
""" 装饰器: 计算函数运行耗时"""
def decorated(*args):
startime = time.time()
func(*args)
endtime = time.time()
taketime = round((endtime - startime)*10**6)
print(f"\n->运算耗时: {taketime} 微秒")
return func(*args)
return decorated
# 本脚本名: des.py
from __util import *
class DES():
""" DES 加解密 """
def __init__(self, scrkey):
self.scrkey = hexToBit(scrkey) # 初始化密钥 16进制字符->比特流 ,也叫种子密钥
def feistel(self, in64bit, flag):
""" Feistel 网络结构算法
@in64bit: 输入64位比特流
@flag: 正向算法/反向算法,正向为1,反向为0
单字符由8比特表示
"""
bit64 = permutate(in64bit, IP) # 初置换IP重排明文
L32b, R32b = bit64[0:32], bit64[32:] # 64位明文左右平分
subkey = createSubKey(self.scrkey) # 生成所有的子密钥
if flag == 0: subkey = subkey[::-1] # 解密用的逆子密钥
for i in range(16):
Fout = turnFunction(R32b, subkey[i])
L32b, R32b = R32b, XOR(L32b, Fout)
out64bit = permutate(R32b + L32b, IP_INV) # 左右交换 逆初始置换
return out64bit
@takeTime
def encrypt(self, messag):
""" DES加密
@messag: 16进制明文字符串
@return: 16进制密文字符串
"""
mesbit = hexToBit(messag)
cipbit = self.feistel(mesbit, 1)
cipher = bitToHex(cipbit)
return cipher
@takeTime
def decrypt(self, cipher):
""" DES 解密
@cipher: 16进制密文字符串
"""
cipher = hexToBit(cipher)
mesbit = self.feistel(cipher, 0)
messag = bitToHex(mesbit)
return messag
if __name__ == '__main__':
scrkey = "133457799BBCDFF1"
messag = "0123456789ABCDEF"
cipher = "85E813540F0AB405"
crypto = DES(scrkey)
print("16进制密文:", crypto.encrypt(messag))
print("16进制明文:", crypto.decrypt(cipher))
参考
https://www.bilibili.com/video/BV1KQ4y127AT/?spm_id_from=333.880.my_history.page.click&vd_source=0bd1680dd495123dd54d157e522a2e86
代码来源:
https://blog.csdn.net/Alpherkin/article/details/121198150?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522168929564016800211547104%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=168929564016800211547104&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2allfirst_rank_ecpm_v1~rank_v31_ecpm-7-121198150-null-null.142v88control_2,239v2insert_chatgpt&utm_term=feistel%E5%8A%A0%E8%A7%A3%E5%AF%86%E7%AE%97%E6%B3%95&spm=1018.2226.3001.4187
持续更新中…
[NCTF-2019-Crypto]Reverse
(于2023-09-10记录)
题目描述:
task.py
import os
import pyDes
flag = "NCTF{******************************************}"
key = os.urandom(8)
d = pyDes.des(key)
cipher = d.encrypt(flag.encode())
with open('cipher', 'wb') as f:
f.write(cipher)
# Leak: d.Kn[10] == [0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1]
cipher.txt
汮S賳!Ⅳ?Z_l,?漋& hDa莸&5匼?oZ€|U€骸%#}巴
记录佬的分析:
大致流程图:
leak中泄露出的Kn[10]应该是11组子密钥K11,逆一下从C11 D11得到K11的PC_2过程(即图中的PERMUTED CHOICE 2过程)就可得到C11 D11
不过C11 D11是56位,K11是48位,所以得爆一下另外8位
再沿着此流程顺下去(Ci,Di经过16次LEFT SHIFTS后会复原),就可以恢复出所有子密钥。
exp:文章来源地址https://www.toymoban.com/news/detail-560953.html
from base64 import b64decode
from itertools import product
from DES import * # https://github.com/soreatu/Cryptography/blob/master/DES.py
guess_8bit = list(product(range(2), repeat=8))
not_in_PC2 = [9,18,22,25,35,38,43,54]
def re_PC2(sbkey):
# 48-bit -> 56-bit
res = [0]*56
for i in range(len(sbkey)):
res[PC_2_table[i]-1] = sbkey[i]
return res # ok
def guess_CiDi10(sbkey, t):
res = re_PC2(sbkey)
for i in range(8):
res[not_in_PC2[i]-1] = guess_8bit[t][i]
return res # ok
def guess_allsbkey(roundkey, r, t):
sbkey = [[]]*16
sbkey[r] = roundkey
CiDi = guess_CiDi10(roundkey, t)
Ci, Di = CiDi[:28], CiDi[28:]
for i in range(r+1,r+16):
Ci, Di = LR(Ci, Di, i%16)
sbkey[i%16] = PC_2(Ci+Di)
return sbkey # ok
def long_des_enc(c, k):
assert len(c) % 8 == 0
res = b''
for i in range(0,len(c),8):
res += DES_enc(c[i:i+8], k)
return res
def try_des(cipher, roundkey):
for t in range(256):
allkey = guess_allsbkey(roundkey, 10, t)
plain = long_des_enc(cipher, allkey[::-1])
if plain.startswith(b'NCTF'):
print(plain)
if __name__ == "__main__":
cipher = b64decode(b'm0pT2YYUIaL0pjdaX2wsxwedViYAaBkZA0Rh3bUmNYVclBlvWoB8VYC6oSUjfbDN')
sbkey10 = [0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1]
try_des(cipher, sbkey10)
# b'NCTF{1t_7urn3d_0u7_7h47_u_2_g00d_@_r3v3rs3_1snt}'
[NepCTF-2023-Crypto]simple_des
(于2023-09-10记录)
题目描述:
from operator import add
from typing import List
from functools import reduce
from gmpy2 import *
from Crypto.Util.number import *
_IP = [57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7,
56, 48, 40, 32, 24, 16, 8, 0,
58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6
]
def IP(plain: List[int]) -> List[int]:
return [plain[x] for x in _IP]
__pc1 = [56, 48, 40, 32, 24, 16, 8,
0, 57, 49, 41, 33, 25, 17,
9, 1, 58, 50, 42, 34, 26,
18, 10, 2, 59, 51, 43, 35,
62, 54, 46, 38, 30, 22, 14,
6, 61, 53, 45, 37, 29, 21,
13, 5, 60, 52, 44, 36, 28,
20, 12, 4, 27, 19, 11, 3
]
__pc2 = [
13, 16, 10, 23, 0, 4,
2, 27, 14, 5, 20, 9,
22, 18, 11, 3, 25, 7,
15, 6, 26, 19, 12, 1,
40, 51, 30, 36, 46, 54,
29, 39, 50, 44, 32, 47,
43, 48, 38, 55, 33, 52,
45, 41, 49, 35, 28, 31
]
ROTATIONS = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1]
def PC_1(key: List[int]) -> List[int]:
return [key[x] for x in __pc1]
def PC_2(key: List[int]) -> List[int]:
return [key[x] for x in __pc2]
def get_sub_key(key: List[int]) -> List[List[int]]:
key = PC_1(key)
L, R = key[:28], key[28:]
sub_keys = []
for i in range(16):
for j in range(ROTATIONS[i]):
L.append(L.pop(0))
R.append(R.pop(0))
combined = L + R
sub_key = PC_2(combined)
sub_keys.append(sub_key)
print('LL=',L[:19])
print('Rr=',R)
return sub_keys
__ep = [31, 0, 1, 2, 3, 4,
3, 4, 5, 6, 7, 8,
7, 8, 9, 10, 11, 12,
11, 12, 13, 14, 15, 16,
15, 16, 17, 18, 19, 20,
19, 20, 21, 22, 23, 24,
23, 24, 25, 26, 27, 28,
27, 28, 29, 30, 31, 0
] # 咦,看出来此表不同之处吗
__p = [15, 6, 19, 20, 28, 11, 27, 16,
0, 14, 22, 25, 4, 17, 30, 9,
1, 7, 23, 13, 31, 26, 2, 8,
18, 12, 29, 5, 21, 10, 3, 24
]
def EP(data: List[int]) -> List[int]:
return [data[x] for x in __ep]
def P(data: List[int]) -> List[int]:
return [data[x] for x in __p]
__s_box = [
[
[14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7],
[ 0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8],
[ 4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0],
[15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13]
],
[
[15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10],
[ 3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5],
[ 0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15],
[13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9]
],
[
[10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8],
[13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1],
[13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7],
[ 1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12]
],
[
[ 7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15],
[13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9],
[10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4],
[ 3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14]
],
[
[ 2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9],
[14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6],
[ 4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14],
[11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3]
],
[
[12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11],
[10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8],
[ 9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6],
[ 4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13]
],
[
[ 4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1],
[13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6],
[ 1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2],
[ 6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12]
],
[
[13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7],
[ 1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2],
[ 7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8],
[ 2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11]
]
]
def S_box(data: List[int]) -> List[int]:
output = []
for i in range(0, 48, 6):
row = data[i] * 2 + data[i + 5]
col = reduce(add, [data[i + j] * (2 ** (4 - j)) for j in range(1, 5)])
output += [int(x) for x in format(__s_box[i // 6][row][col], '04b')]
return output
def encrypt(plain: List[int], sub_keys: List[List[int]]) -> List[int]:
plain = IP(plain)
L, R = plain[:32], plain[32:]
for i in range(16):
prev_L = L # L0
L = R # L1 = R0
expanded_R = EP(R)
xor_result = [a ^ b for a, b in zip(expanded_R, sub_keys[i])]
substituted = S_box(xor_result)
permuted = P(substituted)
R = [a ^ b for a, b in zip(permuted, prev_L)] # R1
cipher = R + L
cipher = [cipher[x] for x in [39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25,
32, 0, 40, 8, 48, 16, 56, 24]]
return cipher
def bitxor(plain1: List[int], plain2: List[List[int]]) -> List[int]:
return [int(i) for i in bin(int(''.join(str(i) for i in plain1),2)^int(''.join(str(i) for i in plain2),2))[2:].zfill(64)]
#key的字母表为abcdefghijklmnopqrstuvwsyz
from secret import flag, key
t=[]
z=[[0]*64]
# z = [[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
key = reduce(add, [list(map(int, bin(key_byte)[2:].zfill(8))) for key_byte in key]) # 转为2进制列表,列表中每个1,0为int型
for i in range(0,3):
pt = reduce(add, [list(map(int, bin(flag_byte)[2:].zfill(8))) for flag_byte in flag[ 8*i:8*(i+1) ]])
ct = encrypt(pt, get_sub_key(bitxor(z[i],key)))
z.append(pt)
t += ct
print(t)
'''
i=0情况下的LL,Rr
LL= [0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
Rr= [0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0]
t=[0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0]
'''
题目实现了一个经典的DES加密算法,除了第一组,后面两组加密时都会密钥都会先和前一组的明文异或。题目给出了第一组加密时的最后一轮轮密钥(L部分少了9bits,可以爆破)
from base64 import b64decode
from itertools import product
from DES import * # https://github.com/soreatu/Cryptography/blob/master/DES.py
from typing import List
guess_8bit = list(product(range(2), repeat=8))
not_in_PC2 = [9,18,22,25,35,38,43,54]
def re_PC2(sbkey):
# 48-bit -> 56-bit
res = [0]*56
for i in range(len(sbkey)):
res[PC_2_table[i]-1] = sbkey[i]
return res # ok
def guess_CiDi10(sbkey, t):
res = re_PC2(sbkey)
for i in range(8):
res[not_in_PC2[i]-1] = guess_8bit[t][i]
return res # ok
def guess_allsbkey(roundkey, r, t):
sbkey = [[]]*16
sbkey[r] = roundkey
CiDi = guess_CiDi10(roundkey, t)
Ci, Di = CiDi[:28], CiDi[28:]
for i in range(r+1,r+16):
Ci, Di = LR(Ci, Di, i%16)
sbkey[i%16] = PC_2(Ci+Di)
if i%16 == 0:
combined = Ci+Di
return combined,sbkey # ok
def long_des_enc(c, k):
assert len(c) % 8 == 0
res = b''
for i in range(0,len(c),8):
res += DES_enc(c[i:i+8], k)
return res
def try_des(cipher, roundkey):
for t in range(256):
combined,allkey = guess_allsbkey(roundkey, 15, t)
plain = long_des_enc(cipher, allkey[::-1])
if plain.startswith(b'Nep'):
print(combined,plain)
exit()
def PC_2(key: List[int]) -> List[int]:
return [key[x] for x in __pc2]
__pc2 = [
13, 16, 10, 23, 0, 4,
2, 27, 14, 5, 20, 9,
22, 18, 11, 3, 25, 7,
15, 6, 26, 19, 12, 1,
40, 51, 30, 36, 46, 54,
29, 39, 50, 44, 32, 47,
43, 48, 38, 55, 33, 52,
45, 41, 49, 35, 28, 31
]
from Crypto.Util.number import *
tt=[0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0]
t = tt[:64]
t = ''.join(str(i) for i in t)
t= int(t,2)
t = long_to_bytes(t)
LL= [0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
Rr= [0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0]
from tqdm import *
for i in range(2**9-1,2**7,-1):
tmp = list(bin(i)[2:].rjust(9,'0'))
L = LL + [ int(u) for u in tmp]
R = Rr
combined = L+R
sub_key = PC_2(combined)
try_des(t, sub_key)
# [0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0] b'NepCTF{N'
得到第一组明文:NepCTF{N,顺便输出了第一组加密过程中的第一轮轮密钥combined
然后拿着第一组的明文NepCTF{N,做一个密钥生成那里的 PC_1置换,再左右两边各自向左循环移位一下,再异或第一轮轮密钥combined,并不是key,不过也可以看成是一个不变的的特征,相当于key的一个小变换,处理得当可以直接用它而不需要用key(这里可以好好理解一下,表置换和移位并不会影响数据本身,故后面再来异或并不会改变结果),就可以解密出第二组密文,以此类推得到第三组明文,全部拼接得到最终flag
from DES import *
from Crypto.Util.number import *
def long_des_enc(c, k):
assert len(c) % 8 == 0
res = b''
for i in range(0,len(c),8):
res += DES_enc(c[i:i+8], k)
return res
def attack(p, c):
combined = [0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0,
1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0]
p = bin(p)[2:].rjust(64, '0')
p = [int(i) for i in p]
# 对明文 PC_1 置换
P = PC_1(p)
# 对明文左右两部分进行第一轮的循环移位
Ci, Di = LR(P[:28], P[28:], 0)
P = Ci + Di
CiDi = []
for i in range(56):
CiDi.append(P[i] ^ combined[i]) # 变换后的p与变换后的key异或,很妙(不需要直接用key)
# 生成所有轮密钥
Ci, Di = CiDi[:28], CiDi[28:]
sbkey = [[]] * 16
sbkey[0] = PC_2(Ci + Di)
r = 1
for i in range(r, r + 16):
Ci, Di = LR(Ci, Di, i % 16)
sbkey[i % 16] = PC_2(Ci + Di)
# 解密密文
c = ''.join(str(i) for i in c)
c = int(c, 2)
c = long_to_bytes(c)
return long_des_enc(c, sbkey[::-1])
tt = [0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0,
1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0,
1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0,
0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1,
0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0,
1, 0]
flag = b"NepCTF{N"
for i in range(2):
t = tt[64 * i + 64:64 * i + 128]
p = flag[i * 8:i * 8 + 8]
flag += attack(bytes_to_long(p), t)
print(flag)
# b'NepCTF{Nep_d0wn_ddddd1s}'
第一次接触这种题,耐心看吧,看懂了真的很有成就感。但看不看得懂是一回事,做不做不出又是一回事,希望下次遇到这种题能别像如今这样无从下手了。
官方wp太复杂了,不想看
题目分析来源:
https://blog.soreatu.com/posts/intended-solution-to-crypto-problems-in-nctf-2019/#reverse909pt-2solvers
https://jayxv.github.io/2023/08/14/2023%20NepCTF/
[极客大挑战-2023] Simple3DES
(于2023-12-15记录)
题目描述:
from Crypto.Cipher import DES3
from Crypto.Util.number import *
import os
import random
import string
import hashlib
xor = lambda a,b: bytes([a[i % len(a)] ^ b[i % len(b)] for i in range(max(len(a), len(b)))])
pad = lambda msg,padlen: msg+chr((padlen-(len(msg)%padlen))).encode()*(padlen-(len(msg)%padlen))
flag = os.environ.get("FLAG", "SYC{Al3XEI_FAKE_FLAG}").encode()
sec = os.urandom(8)
banner = '|'*70
DEBUG = False
def proof_of_work():
if DEBUG:
return True
proof = ''.join([random.choice(string.ascii_letters+string.digits) for _ in range(20)])
digest = hashlib.sha256(proof.encode()).hexdigest()
print("sha256(XXXX+%s) == %s" % (proof[4:], digest))
x = input("Give me XXXX: ")
if len(x)!=4 or hashlib.sha256((x+proof[4:]).encode()).hexdigest() != digest:
return False
print("Right!")
return True
def enc(msg,key):
try:
key = long_to_bytes(key)
msg = xor(long_to_bytes(msg),sec)
des = DES3.new(key,DES3.MODE_ECB)
ct = xor(des.encrypt(pad(msg,8)),sec)
return bytes_to_long(ct)
except Exception as e:
print(e)
return Exception
def service():
cnt = 0
if not proof_of_work():
exit()
print(banner)
print('Simple DES Encryption Service')
print(banner)
while cnt<2:
print('1. Encrypt\n2. Get encrypted flag.')
choice = int(input('> '))
if choice == 1:
print('Input msg:')
msg = int(input('> ').strip())
print('Input key:')
key = int(input('> ').strip())
print(enc(msg,key))
elif choice == 2:
print('Input key:')
key = int(input('> ').strip())
print(enc(bytes_to_long(flag),key))
else:
exit()
cnt+=1
print(banner)
print('Bye!')
exit()
try:
service()
except Exception:
print("Something goes wrong...\n")
print(banner+'\n')
exit()
题目分析:
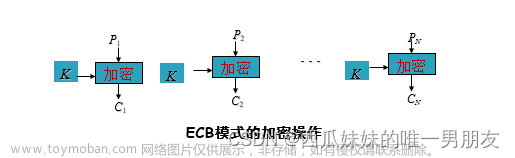
3DES加密流程如下
3DES也是三重DES,是为了增加DES的强度,将DES重复3次所得到的一种加密算法。
由于DES密钥长度实质上是56bit,因此三重DES的密钥长度就是3*56=168 bit
题目中
输入1,我们自己确定明文和密钥并得到明文加密后的密文
输入2,我们自己确定密钥并得到flag加密后的密文
两层循环,那就是1,2都输一遍喽
加密代码:
def enc(msg,key):
try:
key = long_to_bytes(key)
msg = xor(long_to_bytes(msg),sec)
des = DES3.new(key,DES3.MODE_ECB)
ct = xor(des.encrypt(pad(msg,8)),sec)
return bytes_to_long(ct)
except Exception as e:
print(e)
return Exception
可以看出过程是:
明文和sec异或
异或后的数据进行填充,然后进行3DES加密
加密后的数据再与sec异或
其中sec我们不知道,不过注意sec为8bit
而后面明文会进行长度为8的填充
pad:
pad = lambda msg,padlen: msg+chr((padlen-(len(msg)%padlen))).encode()*(padlen-(len(msg)%padlen))
我们都知道DES为块加密,64位为一组进行加密,正好8字节
所以这里我们密文输入8的整数倍,那么可以知道最后8个为0
这样的话我们key知道,明文填充后最后8字节知道,那么可以通过加密函数得到明文填充后密文,又ct = sec ^ 明文填充后密文,其中ct知道,这样sec也就出来了
sec求出之后,flag也就差不多出了(后面很简单,应该知道怎么求,我就不说了)
如果密文直接输入空,那么3DES加密的数据就是padding(sec,8),后面流程其实也差不多
看到一个非预期解,这里记录一下:弱密钥
就是说,在DES中,存在一些密钥,被处理后会使得16轮轮密钥完全相等,这种便称为弱密钥
这种的话,加密一次看起来很正常,不过再加密一次便能重新得到明文,反之亦然
四个弱密钥:
\x01\x01\x01\x01\x01\x01\x01\x01
\xFE\xFE\xFE\xFE\xFE\xFE\xFE\xFE
\xE0\xE0\xE0\xE0\xF1\xF1\xF1\xF1
\x1F\x1F\x1F\x1F\x0E\x0E\x0E\x0E
由于DES密钥长度实质上是56bit,因此三重DES的密钥长度就是3*56=168 bit
故我们可以构造如下密钥:
key = b'\x01\x01\x01\x01\x01\x01\x01\x01' + b'\xFE\xFE\xFE\xFE\xFE\xFE\xFE\xFE' + b'\x01\x01\x01\x01\x01\x01\x01\x01'
第一次输入2,输入上面的key,得到flag的加密值
第二次输入1,输入上面的key,再输入flag的加密值,得到flag加密两次得到原值
想了解更多des的秘密,看这里
想了解des中的弱密钥,看这里
[moectf-2023] feistel
题目描述:
from Crypto.Util.number import *
def f(m, key):
m = m ^ (m >> 4)
m = m ^ (m << 5)
m = m ^ (m >> 8)
m ^= key
m = (m * 1145 + 14) % 2**64
m = (m * 1919 + 810) % 2**64
m = (m * key) % 2**64
return m
def dec(c,key):
key = bytes_to_long(key)
left = bytes_to_long(c[:8])
right = bytes_to_long(c[8:])
m_right = f(right,key) ^ left
m_left = f(m_right,key) ^ right
return long_to_bytes(m_left) + long_to_bytes(m_right)
def ecb_dec(c, key):
clen = len(c)
m = b""
for i in range(clen // 16):
m += dec(c[i * 16 : i * 16 + 16], key)
return m
c = b'\x0b\xa7\xc6J\xf6\x80T\xc6\xfbq\xaa\xd8\xcc\x95\xad[\x1e\'W5\xce\x92Y\xd3\xa0\x1fL\xe8\xe1"^\xad'
key = b"wulidego"
flag = ecb_dec(c,key)
print(flag)
题目分析:
feistel加密结构,加解密过程一样,就是轮密钥相反
而这里每轮密钥都是wulidego,所以说这个加解密是完全一样的
exp:
from Crypto.Util.number import *
round = 2
def f(m, key):
m = m ^ (m >> 4)
m = m ^ (m << 5)
m = m ^ (m >> 8)
m ^= key
m = (m * 1145 + 14) % 2**64
m = (m * 1919 + 810) % 2**64
m = (m * key) % 2**64
return m
def enc(m, key, round):
key = bytes_to_long(key)
left = bytes_to_long(m[:8])
right = bytes_to_long(m[8:])
for i in range(round):
left, right = right, f(right, key) ^ left
left, right = right, left
return long_to_bytes(left).rjust(8, b"\x00") + long_to_bytes(right).rjust(8, b"\x00")
def padding(m):
mlen = len(m)
pad = 16 - mlen % 16
return m + pad * bytes([pad])
def ecb_enc(m, key):
m = padding(m)
mlen = len(m)
c = b""
for i in range(mlen // 16):
c += enc(m[i * 16 : i * 16 + 16], key, round) # round = 2
return c
def ecb_dec(m, key):
m = padding(m)
mlen = len(m)
c = b""
for i in range(mlen // 16):
c += enc(m[i * 16 : i * 16 + 16], key, round) # round = 2
return c
c = b'\x0b\xa7\xc6J\xf6\x80T\xc6\xfbq\xaa\xd8\xcc\x95\xad[\x1e\'W5\xce\x92Y\xd3\xa0\x1fL\xe8\xe1"^\xad'
print(ecb_enc(c,b'wulidego'))
# moectf{M@g1cA1_Encr1tion!!!}
[moectf-2023] feistel_promax
题目描述:
from Crypto.Util.number import *
from os import urandom
round = 2
flag = open("./secret", "rb").read().strip()
def f(m, key):
m = m ^ (m >> 4)
m = m ^ (m << 5)
m = m ^ (m >> 8)
m ^= key
m = (m * 1145 + 14) % 2**64
m = (m * 1919 + 810) % 2**64
m = (m * key) % 2**64
return m
def enc(m, key, round):
key = bytes_to_long(key)
left = bytes_to_long(m[:8])
right = bytes_to_long(m[8:])
for i in range(round):
left, right = right, f(right, key) ^ left
left, right = right, left
return long_to_bytes(left).rjust(8, b"\x00") + long_to_bytes(right).rjust(8, b"\x00")
def padding(m):
mlen = len(m)
pad = 16 - mlen % 16
return m + pad * bytes([pad])
def ecb_enc(m, key):
mlen = len(m)
c = b""
for i in range(mlen // 16):
c += enc(m[i * 16 : i * 16 + 16], key, round)
return c
key = urandom(8)
print(ecb_enc(padding(flag), key))
# b'B\xf5\xd8gy\x0f\xaf\xc7\xdf\xabn9\xbb\xd0\xe3\x1e0\x9eR\xa9\x1c\xb7\xad\xe5H\x8cC\x07\xd5w9Ms\x03\x06\xec\xb4\x8d\x80\xcb}\xa9\x8a\xcc\xd1W\x82[\xd3\xdc\xb4\x83P\xda5\xac\x9e\xb0)\x98R\x1c\xb3h'
相比于上一题,这题key不知,仅根据此条件根本无从下手,不过观察仔细的话会发现最后一行,加密的主体是padding(flag),而加密过程中又进行了一次padding,所以说进行了两次padding
故:
padding(padding(m)) = b'****' + b'\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10'
又有以下过程:
初始
:
m
[
:
8
]
+
m
[
8
:
]
第一轮
:
m
[
8
:
]
+
f
(
m
[
8
:
]
,
k
e
y
)
⊗
m
[
:
8
]
第二轮
:
f
(
m
[
8
:
]
,
k
e
y
)
⊗
m
[
:
8
]
+
f
(
f
(
m
[
8
:
]
,
k
e
y
)
⊗
m
[
:
8
]
,
k
e
y
)
⊗
m
[
8
:
]
再交换最后得到
:
f
(
f
(
m
[
8
:
]
,
k
e
y
)
⊗
m
[
:
8
]
,
k
e
y
)
⊗
m
[
8
:
]
+
f
(
m
[
8
:
]
,
k
e
y
)
⊗
m
[
:
8
]
\begin{gathered} \text{初始}:m[:8]+m[8:] \\ \text{第一轮}:m[8:]+f(m[8:],key)\otimes m[:8] \\ \text{第二轮}:f(m[8:],key)\otimes m[:8]+f(f(m[8:],key)\otimes m[:8],key)\otimes m[8:] \\ \text{再交换最后得到}:f(f(m[8:],key)\otimes m[:8],key)\otimes m[8:]+\boxed{f(m[8:],key)\otimes m[:8]} \end{gathered}
初始:m[:8]+m[8:]第一轮:m[8:]+f(m[8:],key)⊗m[:8]第二轮:f(m[8:],key)⊗m[:8]+f(f(m[8:],key)⊗m[:8],key)⊗m[8:]再交换最后得到:f(f(m[8:],key)⊗m[:8],key)⊗m[8:]+f(m[8:],key)⊗m[:8]
不过最后还是没很大思路,参考此文:https://dexterjie.github.io/2023/09/25/%E8%B5%9B%E9%A2%98%E5%A4%8D%E7%8E%B0/2023MoeCTF/#feistel-promax
我们以最后一组来分析,最后一组加密明文:b'\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10\x10'
故
f
(
m
[
8
:
]
,
k
e
y
)
⊗
m
[
:
8
]
f(m[8:],key)\otimes m[:8]
f(m[8:],key)⊗m[:8]中m[8:] = m[:8]
所以能有以下爆破文章来源:https://www.toymoban.com/news/detail-560953.html
exp:
from Crypto.Util.number import *
round = 2
def f(m, key):
m = m ^ (m >> 4)
m = m ^ (m << 5)
m = m ^ (m >> 8)
m ^= key
m = (m * 1145 + 14) % 2**64
m = (m * 1919 + 810) % 2**64
m = (m * key) % 2**64
return m
def dec(m, key, round):
key = bytes_to_long(key)
left = bytes_to_long(m[:8])
right = bytes_to_long(m[8:])
for i in range(round):
left, right = right, f(right, key) ^ left
left, right = right, left
return long_to_bytes(left).rjust(8, b"\x00") + long_to_bytes(right).rjust(8, b"\x00")
def ecb_dec(c, key):
clen = len(c)
m = b""
for i in range(clen // 16):
m += dec(c[i * 16 : i * 16 + 16], key, 2)
return m
m = b'\x10\x10\x10\x10\x10\x10\x10\x10'
ct = b'B\xf5\xd8gy\x0f\xaf\xc7\xdf\xabn9\xbb\xd0\xe3\x1e0\x9eR\xa9\x1c\xb7\xad\xe5H\x8cC\x07\xd5w9Ms\x03\x06\xec\xb4\x8d\x80\xcb}\xa9\x8a\xcc\xd1W\x82[\xd3\xdc\xb4\x83P\xda5\xac\x9e\xb0)\x98R\x1c\xb3h'
c = bytes_to_long(ct[-8:]) ^ bytes_to_long(m)
bin_c = bin(c)[2:].rjust(64,'0') # = f(M[8:],key),其中M = m * 2
k1 = [b'']
for i in range(1,5):
k2 = []
for KEY in k1:
for j in range(2**16):
key1 = long_to_bytes(j) + KEY
cc = f(bytes_to_long(m),bytes_to_long(key1)) # = f(M[8:],key)
bin_cc = bin(cc)[2:].rjust(64,'0')
if bin_cc[-16*i:] == bin_c[-16*i:]:
k2.append(key1)
k1 = k2
# print(k1)
# k1= [b'4t*zFD\xac\xb4', b'\xb4t*zFD\xac\xb4', b'\\q\x0f\x00w\xeb\xc1"', b'\xdcq\x0f\x00w\xeb\xc1"']
for KEY in k1:
flag = ecb_dec(ct,KEY)
print(flag)
# moectf{F_func_1s_n1t_Ve5y_$EcU%e}
到了这里,关于DES加密解密 Feistel算法网络结构 详讲的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!