机器学习 day27（反向传播）-Toy模板网

这篇具有很好参考价值的文章主要介绍了机器学习 day27（反向传播）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

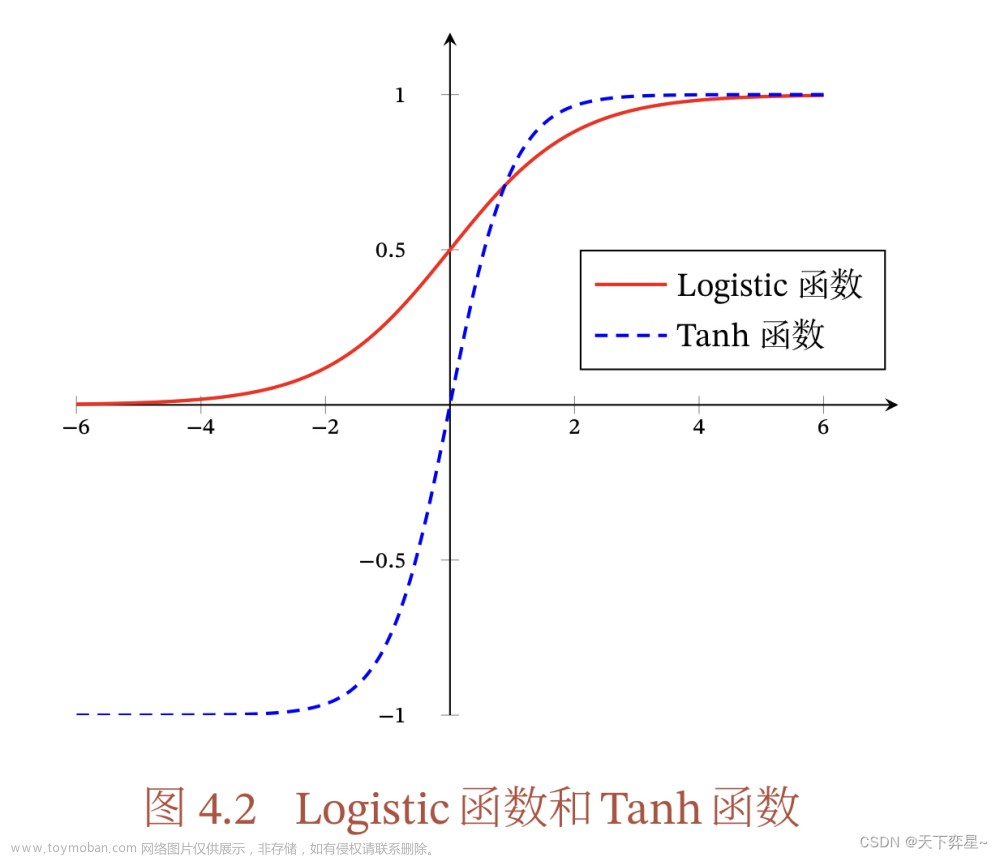
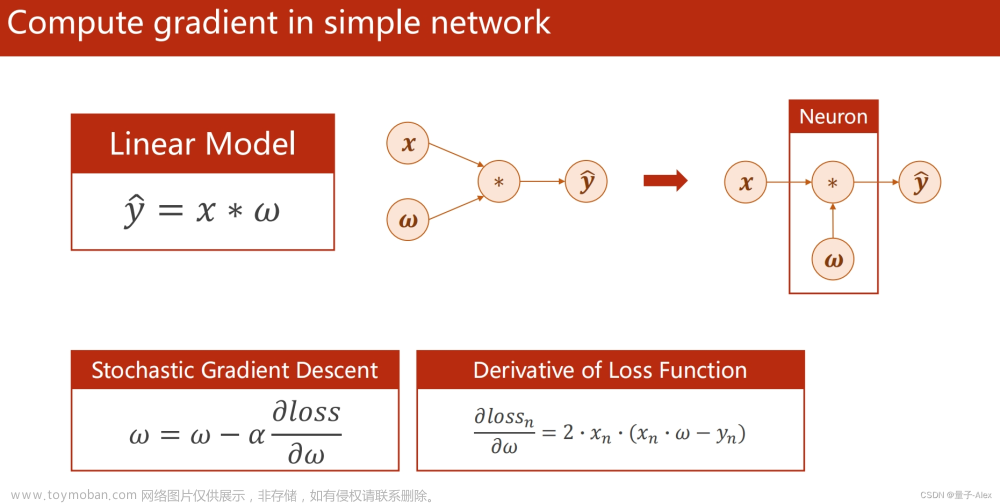
1. 导数
机器学习 day27（反向传播）,学习,机器学习

2. 反向传播
机器学习 day27（反向传播）,学习,机器学习

tensorflow中的计算图，由有向边和节点组成。从左向右为正向传播，神经网络模型使用正向传播来输出结果
从右向左为反向传播，tensorflow使用反向传播来自动计算神经网络模型中的导数。
反向传播求导数的过程类似链式求导法则，从右往左一层一层的求导，再将导数相乘就是最终的结果。例如：先求当d增加ε时，J增加多少，再求当a增加ε时，J增加多少…，最后把J增加的倍数k乘起来，就是最终的结果

机器学习 day27（反向传播）,学习,机器学习

反向传播是计算导数的有效方法，若要计算J对w的导数，就要知道J对d，d对a，a对c，c对w的导数，这个顺序刚好是从右到左的顺序
反向传播求导数的步数大概是整个模型的节点数n与参数p之和。正向传播求导数的步数则是n与p之积
综上：计算图执行神经网络模型输出成本函数J和导数的步骤为：逐步计算，并把它们分解为计算图的不同节点，使用从左到右（正向传播）来计算成本函数J，通过从右到左（反向传播）来计算所有导数

3. 大型神经网络的计算图
机器学习 day27（反向传播）,学习,机器学习文章来源地址https://www.toymoban.com/news/detail-563539.html

计算图由有向边和节点组成，节点表示数学运算，有向边表示节点间的数据交互。
该神经网络模型求解成本函数的步骤可以用计算图表示
正向传播计算导数的效率很低，对于每一个参数都要执行一次从左往右的正向传播，来计算该参数是如何引起J的变化的。若计算图由n个节点和p个参数，那么正向传播一共需要大约n * p个步骤，效率很低。
反向传播计算导数的效率很高，只需要从右往左执行一次反向传播，再计算J对每一个参数的导数即可，那么反向传播只需要大约n + p个步骤，效率很高