【数据结构】二叉树——链式结构-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构】二叉树——链式结构。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、前置声明

二、二叉树的遍历

2.1 前序、中序以及后序遍历

2.2 层序遍历

三、节点个数以及高度

3.1 节点个数

3.2 叶子节点个数

3.3 第k层节点个数

3.4 二叉树的高度/深度

3.5 查找值为x的节点

四、二叉树的创建和销毁

4.1 构建二叉树

4.2 二叉树销毁

4.3 判断二叉树是否为完全二叉树

该努力的时候不要选择安逸！

一、前置声明

二叉树是： 1. 空树 2. 非空：根节点，根节点的左子树、根节点的右子树组成的。

二叉树定义是递归式的，因此后序基本操作中基本都是按照该概念实现的。

【数据结构】二叉树——链式结构,笔记,初阶数据结构,数据结构,算法,c语言

普通二叉树的增删查改是没有价值的，如果是为了单纯的存储数据，不如使用线性表。

二、二叉树的遍历

遍历方法：前序遍历、中序遍历、后序遍历和层序遍历

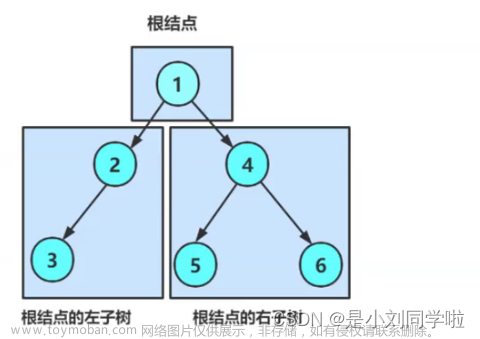
【数据结构】二叉树——链式结构,笔记,初阶数据结构,数据结构,算法,c语言

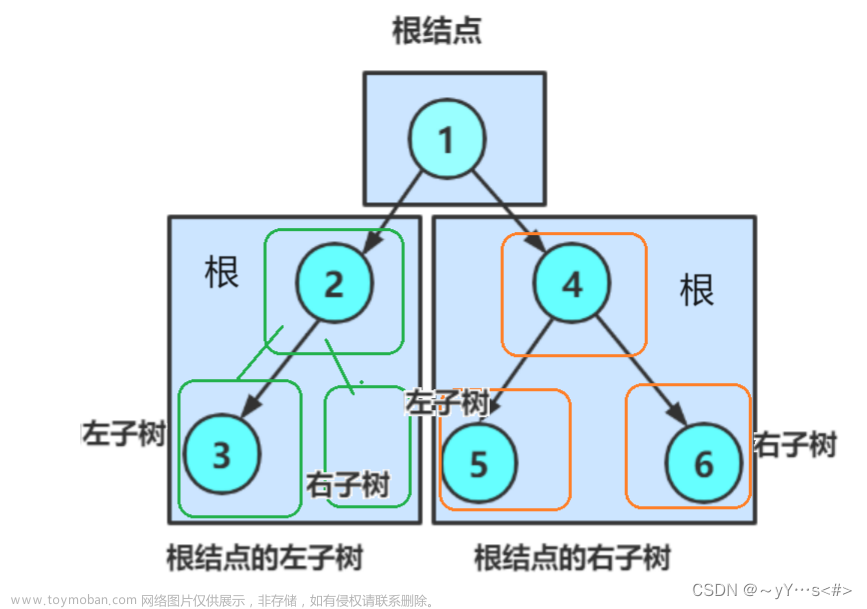
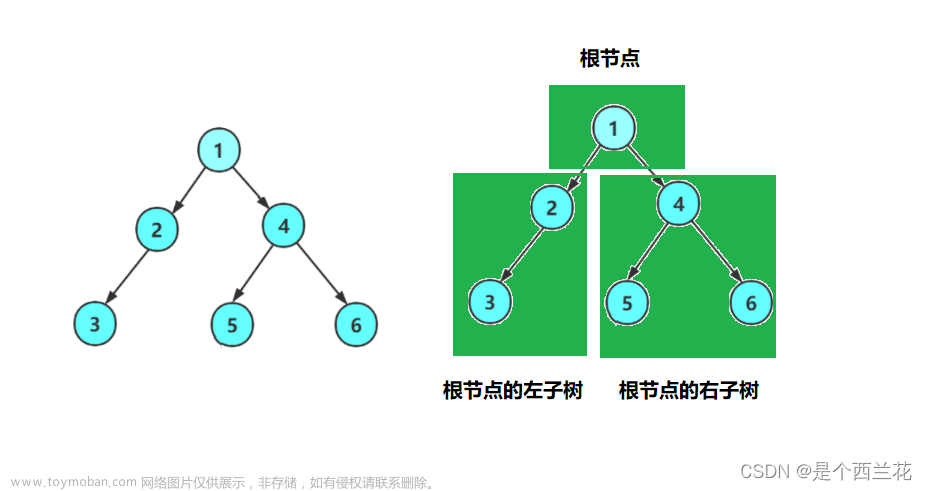
（1）先序遍历（也叫作先根遍历）：（根、左子树、右子树）上图：首先遍历1（根），然后遍历1的左子树2，接着遍历2的左子树3，然后比遍历3的左子树NULL,然后3的右子树NULL；然后遍历2的右子树NULL；在接着遍历1的右子树4，然后遍历4的左子树5，再然后遍历5的左子树NULL，然后5的右子树NULL；接着遍历4的右子树6，最后遍历6的左子树NULL，然后6的右子树。即1->2->3->NULL->NULL->NULL->4->5->NULL->NULL->6->NULL->NULL 【颜色依次是根、左子树、右子树】

（2）中序遍历（中根遍历）：（左子树、根节点、右子树）即：对于3来说，NULL->3->NULL，对于2来说NULL->3->NULL->2->NULL;对于1来说，NULL->3->NULL->2->NULL->1->NULL->5->NULL->4->NULL->6->NULL 【想访问1，就要先访问1的左子树2，想访问2，就要先访问2的左子树3，想访问3，就要先访问3的左子树NULL】

（3）后序遍历（后根遍历）：（左子树、右子树、根子树）：即：NULL->NULL->3->NULL->2->NULL->NULL->5->NULL->NULL>6->4->1

（4）层序遍历（一层一层的）(不需要递归)：即：1->2->4->3->5->6

2.1 前序、中序以及后序遍历

二叉树遍历 (Traversal) 是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。

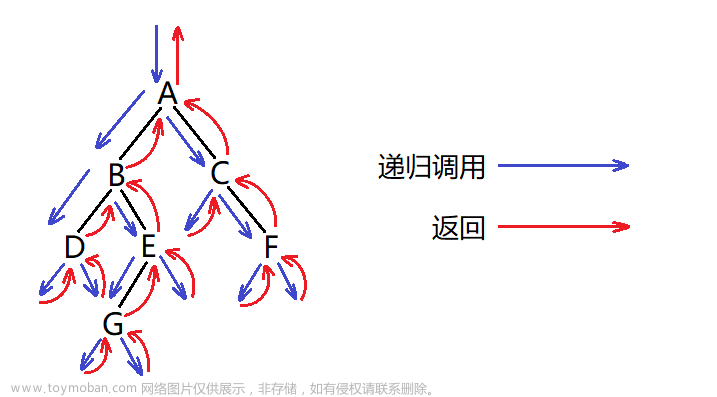
前序/中序/后序的递归结构遍历：

1.前序遍历 (Preorder Traversal 亦称先序遍历 )—— 访问根结点的操作发生在遍历其左右子树之前。

2. 中序遍历 (Inorder Traversal)—— 访问根结点的操作发生在遍历其左右子树之中（间）。

3. 后序遍历 (Postorder Traversal)—— 访问根结点的操作发生在遍历其左右子树之后。

前序遍历结果： 1 2 3 4 5 6

中序遍历结果： 3 2 1 5 4 6

后序遍历结果： 3 2 5 6 4 1

代码：

#include <stdio.h>
#include <stdlib.h>
#include <assert.h>

typedef int BTDataType;

typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}BTNode;

BTNode* BuyBTNode(BTDataType x)
{
	BTNode* node = (BTNode*)malloc(sizeof(BTNode));
	if (node == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	node->left = node->right = NULL;
	node->data = x;
	return node;
}

BTNode* CreatBinaryTree()
{
	BTNode* node1 = BuyBTNode(1);
	BTNode* node2 = BuyBTNode(2);
	BTNode* node3 = BuyBTNode(3);
	BTNode* node4 = BuyBTNode(4);
	BTNode* node5 = BuyBTNode(5);
	BTNode* node6 = BuyBTNode(6);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;
	return node1;
}
//根 左 右
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}

int main()
{
	BTNode* tree = CreatBinaryTree();
	PrevOrder(tree);//前
	printf("\n");
	InOrder(tree);//中序
	printf("\n");
	PostOrder(tree);//后序
	printf("\n");
	return 0;
}

2.2 层序遍历

除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	//首先把根进入到队列里面，
	if (root != NULL)
	{
		QueuePush(&q, root);
	}
	//判断队列是否为空，
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ", front->data);
		//出数据的同时，伴随着进数据
		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	printf("\n");
	QueueDestory(&q);
}

思想：（1）先把根入队列，借助队列先入先出的性质（2）节点出的时候，把下一层非空的节点进入到队列里面。一边进，一边出。

深度优先遍历（DFS）：前序遍历、中序遍历、后序遍历；

广度优先遍历（BFS）：层序遍历

前置声明：如果想使用一个结构体，但是这个结构体在后面定义，就可以使用前置声明（和函数声明一样）struct BinaryTreeNode;

三、节点个数以及高度

3.1 节点个数

思想：遍历+计数

代码1：

//前序遍历
int count = 0;
void BTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	count++;
	BTreeSize(root->left);
	BTreeSize(root->right);
}

int main()
{
    BTNode* tree = CreatBinaryTree();
    count = 0;
	BTreeSize(tree);
	printf("Size = %d", count);
	printf("\n");
	count = 0;
	BTreeSize(tree);
	printf("Size = %d", count);
}

我们比较容易想到的思路是，把遍历二叉树的printf改成 count++;但是，我们要在每一个栈帧里都创建一个count吗？所以我们可以定义一个全局变量count（代码1），但是这个会有多路线程安全问题。所以最佳的方法是增加一个指针。（代码2）

代码2：

void BTreeSize(BTNode* root,int* pcount)
{
	if (root == NULL)
	{
		return;
	}
	(*pcount)++;
	BTreeSize(root->left, pcount);
	BTreeSize(root->right, pcount);
}

int main()
{
	BTNode* tree = CreatBinaryTree();
	int count = 0;
	BTreeSize(tree, &count);
	printf("Size = %d", count);
	return 0;
}

代码3：

int BTreeSize(BTNode* root)
{
	return root == NULL ? 0 : (BTreeSize(root->left) + BTreeSize(root->right) + 1);
}

分治：把复杂的问题，分成更小规模的子问题，子问题再分成更小规模的问题，直到子问题不可再分割，直接能出结果

思路：子问题（1）空树，最小规模子问题，节点个数返回0,（2）非空，左子树节点个数+右子树节点个数+1【自己】【代码3】

即：如果想知道，这个节点的树多少个节点，首先必须知道左子树和右子树的节点个数，然后再加上自己。当这个节点是NULL的时候，返回0即可。

3.2 叶子节点个数

代码1：

void BTreeLeafSize(BTNode* root, int* pcount)
{
	if (root == NULL)
	{
		return;
	}
	if ((root->left == NULL) && (root->right == NULL))
	{
		(*pcount)++;
	}
	BTreeLeafSize(root->left, pcount);
	BTreeLeafSize(root->right, pcount);
}

int main()
{
    int count = 0;
    BTreeLeafSize(tree, &count);
	printf("%d\n", count);
	return 0;
}

思路1：遍历+计数【代码1】

代码2：

int BTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->right == NULL && root->left == NULL)
	{
		return 1;
	}
	return BTreeLeafSize(root->right) + BTreeLeafSize(root->left);
}

int main()
{
    BTreeLeafSize(tree);
	printf("%d\n", BTreeLeafSize(tree));
	return 0;
}

思路2：分治【代码2】

数的叶子节点等于左子树的叶子节点+右子树的叶子节点。一直分到这个小树的根的节点不等于NULL，但是左右子树为NULL。

3.3 第k层节点个数

int BTreeKLevelSize(BTNode* root, int k)
{
	assert(k >= 1);
	if (root == NULL)
	{
	    return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return  BTreeKLevelSize(root->left, k - 1) + BTreeKLevelSize(root->right, k - 1);
}

分治思想：（1）空树，返回0（2）非空，且k==1，返回1（3）非空且K>1,装换成左子树K-1层节点个数+右子树k-1层节点个数。

即：【首先，求第k层节点个数，首先这一层看成满的，如果有节点就返回1，如果没有节点就返回0】其次（1）如果求的是第一层的节点个数，那就直接是1，（2）如果求的是第二层的节点个数，那么可以转化成求左子树的第一层节点个数+右子树的第一层节点个数（3）如果求的是根的第三层的节点个数，那么可以转化成求该根左子树的第二层节点个数+右子树的第二层节点个数，再转化成该根的左子树的左子树的第一层节点个数+该根左子树的右子树的第一层节点个数+根的右子树的左子树的第一层节点个数+该根右子树的右子树的第一层节点个数【第一层（1）空树，返回0（2）k==1，返回1】

3.4 二叉树的高度/深度

int BTreeDepth(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return  BTreeDepth(root->left) > BTreeDepth(root->right) ? (BTreeDepth(root->left) + 1) : (BTreeDepth(root->right) + 1);
}

分治思想：左子树和右子树高度较大的那一个+1.

3.5 查找值为x的节点

BTNode* BTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	BTNode* ret1 = BTreeFind(root->left, x);
	if (ret1)
	{
		return ret1;
	}
	BTNode* ret2 = BTreeFind(root->right, x);
	if (ret2)
	{
		return ret2;
	}
	return NULL;
}

分治思想：【如果左子树找到了，那么右子树就不需要再进行查找】

找到了指针，就可以对其进行改变值

四、二叉树的创建和销毁

4.1 构建二叉树

链接：牛客

代码：

#include <stdio.h>
#include <stdlib.h>
typedef struct BinaryTreeNode
{
    char data;
    struct BinaryTreeNode* left;
    struct BinaryTreeNode* right;
}BTNode;
//先构建一个二叉树【前序遍历】
 BTNode* CreatTree(char* a, int* pi)
 {
    if (a[*pi] == '#')
    {
        (*pi)++;
        return NULL;
    }
    //先构建根
    BTNode* root = (BTNode*)malloc(sizeof(BTNode));
    root->data = a[*pi];
    (*pi)++;
    //再构建左子树和右子树
    root->left = CreatTree(a, pi);
    root->right = CreatTree(a, pi);
    return root;
 }
 
void InOrder(BTNode* root)
{
    if (root == NULL)
    {
        return;
    }
    InOrder(root->left);
    printf("%c ", root->data);
    InOrder(root->right);
}
 
int main()
{
    char a[100];
    scanf("%s", a);
    int i = 0;
    BTNode* tree = CreatTree(a, &i);
    InOrder(tree);
    free(tree);
    tree = NULL;
    return 0;
}

思想：先序遍历的思想的字符串，建立二叉树【遇到'#',就返回NULL】，然后再中序遍历的思想进行打印。

4.2 二叉树销毁

void BTreeDestory(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	BTreeDestory(root->left);
	BTreeDestory(root->right);
	free(root);
}
int main()
{
	BTNode* tree = CreatBinaryTree();
	BTreeDestory(tree);//想改变谁的内容，就需要把谁的地址传递给函数。
	free(tree);
	tree = NULL;
	return 0;
}

（1）后序遍历（2）一级指针，tree需要在函数外面进行销毁。（3）如果传递的是二级指针，就可以在函数内进行销毁。

4.3 判断二叉树是否为完全二叉树

bool BinaryTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		if (front == NULL)
		{
			break;
		}
		QueuePop(&q);
		QueuePush(&q, root->left);//不管是还是不是NULL，都进入队列
		QueuePush(&q, root->right);
	}
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		if (front != NULL)
		{
			QueueDestory(&q);
			return false;
		}
		QueuePop(&q);
	}
	QueueDestory(&q);
	return true;
}

思想：层序遍历的思想；一个节点出队列的时候，会把该节点下一层的节点入队列（把NULL也进入队列），完全二叉树，层序遍历完之后，就不会出现NULL。如果不是完全二叉树，就会出现NULL。

思路：（1）层序遍历，空节点也可以进队列（2）出到空节点以后，出队列中所有数据，如果全是NULL，就是完全二叉树，如果有非空，就不是完全二叉树。