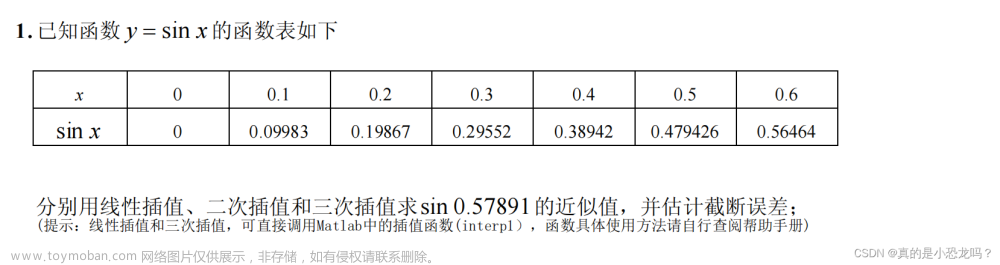
#16 拉格朗日乘数法
所谓拉格朗日乘数法，是一种求条件极值的办法。所谓条件极值，就是在给定的约束条件下，求目标函数的极值。
符号解释：目标函数 u = f ( x , y ) u = f(x,y) u=f(x,y), 约束条件 φ ( x , y ) = 0 \varphi(x,y) = 0 φ(x,y)=0
应用条件： f ( x , y ) f(x,y) f(x,y)和 φ ( x , y ) \varphi(x,y) φ(x,y)一阶偏导数连续（ ⇒ \Rightarrow ⇒可微）
证明：可参考拉格朗日乘数法-wiki
使用方法：
- 构造拉格朗日函数 F ( x , y , λ ) = f ( x , y ) + λ φ ( x , y ) F(x,y,\lambda) = f(x,y)+\lambda \varphi(x,y) F(x,y,λ)=f(x,y)+λφ(x,y)
- 梯度为零，构造方程组： ∇ F = 0 \nabla F = \mathbf{0} ∇F=0
- 解得满足方程组的驻点
- 根据实际情况判断这些点是不是极值点
从使用方法4可以看出，拉格朗日乘数法，求得的点其实仅仅可能是极值点。
举例：证明当离散信源均匀分布的时候熵最大
目标函数： H = − ∑ i = 1 N p i l o g 2 ( p i ) H = -\sum_{i=1}^N p_i log_2(p_i) H=−∑i=1Npilog2(pi)
约束条件： p 1 + p 2 + p 3 + ⋯ + p N = 1 p_1 + p_2 + p_3 + \cdots + p_N = 1 p1+p2+p3+⋯+pN=1，且 p i > 0 p_i > 0 pi>0
证明：文章来源：https://www.toymoban.com/news/detail-566365.html
文章来源地址https://www.toymoban.com/news/detail-566365.html
到了这里，关于【高等数学】拉格朗日乘数法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
