TOPSIS法(Technique for Order Preference by Similarity to ldeal Solution)
可翻译为逼近理想解排序法,国内常简称为优劣解距离法
TOPSIS法是一种常用的综合评价方法,其能充分利用原始数据的信息,其结果能精确的反应各评价方案之间的差距。
(上期我们刚讲述了层次分析法,但是对于层次分析法也有一定的限制)
层次分析法的局限性:
那TOPSIS法如何评分呢?
我们的成绩有时是分数越高对于我们越好,但当统计其它事物时,如情商(我们通过与人正常次数来做判断,争吵次数越多情商越低)这样就会出现了我们评价指标有时越大越好有时越小越好对此我们作出定义:
但每次的指标步同我们的统计的方法也会随之改变所以我们定义了将所有的指标都转换为极大型指标方便我们统计:
也就是我们TOPSOSIS法的第一步: 指标正向化
这里将数据正向化分为极小型正向化,中间型正向化,区间型正向化
(由于内容过多防止读者理解混乱我们先介绍大体的TOPSIS的步骤,最后再去讲正向化细节)
第二步:对正向化后的矩阵进行标准化
为了消去不同指标量纲的影响,需要对已经正向化的矩阵进行标准化处理。
标准化处理的解释就是:每一个元素/[(其所在列的元素的平方和)再开根号]
设X(n行,m列)为我们需要处理的数据矩阵。(n为评价目标的个数,m为评价指标的个数)
(接下来直接上matlab代码,为了大家理解的更清晰,将一行一行代码拆成小部分来解析)
- 求其所在列的平方和 sum(X.*X).
- 开根号sum(X.*X).^0.5
[a.b完成后我们得到了一行m列的向量。为了让每个元素都标准化(/每列平方和的根号)我们需要将的得到的这个向量复制成和X大小一样的矩阵,方便计算。]
c.复制矩阵Y=repmat(sum(X.*X).^0.5,n,1)将得到的结果复制n行使其成为与X相同形状。
d.标准化矩阵Z=X./Y;

第三步计算得分并归一化
构造评分方式,方便结果更加符合实际情况
文字描绘:
计算得分的公式(也是我们在写代码时实现的方法)

Z即是我们第二部求出来的标准化方阵
为了方便我们将z与最大值距离定义为D_P,最小值距离定义为D-N
D_P= sum([(Z-repmat(max(Z),n,1)) .^2],2) .^0.5;
Z与max的d:[(每个元素-所在列的max)的平方得到的矩阵按行求和]再开根号
D_P= sum([(Z-repmat(min(Z),n,1)] .^2],2) .^0.5;
Z与min的d:[(每个元素-所在列的min)的平方得到的矩阵按行求和]再开根号
得到D_P&&D_N后我们可以计算对评价对象未归一化的得分:
S=D_N/(D_P+D_N);
最后归一化S得到最后的评分:(S是一个n行1列的向量,对n个评价对象的评分)
Stand_S=S/sum(S);
为了便于我们的观察我们最后通过sort函数将评分排序
(由于是分越高越好所以我们逆序排序(由大到小)所以矩阵后面要加上‘descend‘)
[sotred_s,index]=sort(stand_S,’descend)
(当sort函数有两个接受值的时候,第一个接收值是排序后的数列,第二个接收值是排序好的数列在原数列的下标,这样方便我们直接找到原数据中那个是第一名)
各种评价类型正向化的方法:
最常见的四种指标:
- 极小型指标=>正向化
矩阵中的最大值-每个元素形成的矩阵
- 中间型指标=>正向化
根据题目或者我们给定一个中间值:best
定义M:|每个元素-best|的绝对值,其中的最大值
1-(|每个元素-best的绝对值|/M)后得到的矩阵
- 区间型指标=>正向化
题目给出或我们天给定最佳区间的区间下限a,和区间上限b
定义M=max{(a-最小元素),(最大元素-b)}
每个元素:
- 如果 x<a , xi = 1 - (a-x) / M;
- 如果 a<=x<=b , xi = 1;
- 如果 x>b , xi = 1 -(x-b)/ M;
后的得到的矩阵。
列题以及代码实现和讲解:
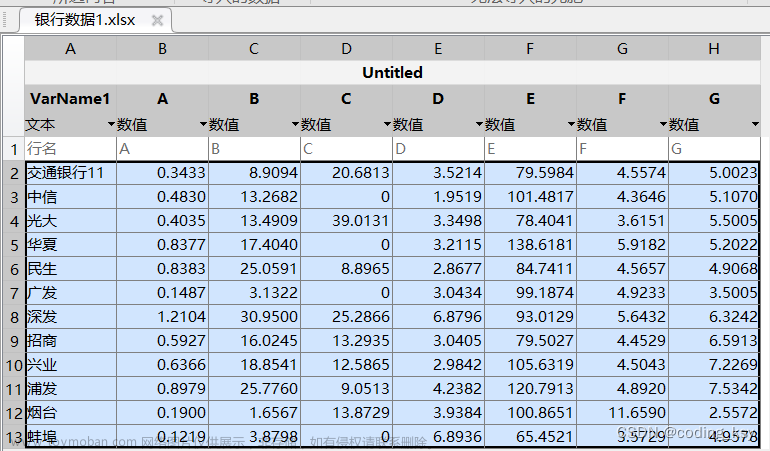
题目分析:本题让我们根据给出的四个之变让我们对A-T这20个对象评分。
但由于指标2,3,4都不是极大型指标所以我们需要正向化。
代码实现:
-
我们需要将数据导入到matlab中:我们只需要将Excle中的B2:E21导入到matlab中

操作步骤:我们在matlab的工作区右击点新建形成有一个新文件我们点开后会出现一个跟exlce一样的表格我们点复制即可(别忘了重命名)
- 导入我们的数据,求其行和列
- 根据我们数据指标的类型判断是否需要正向化以及那些列需要正向化
这里我们正向化需要自定义函数。
Matlab中自定义函数不能和主函数在一个脚本中,需要新建一个脚本专门来写自定义函数,且自定义函数的脚本必须和主函数保存在一个文件夹中。
Matlab自定义函注意事项:和c一样主函数中写接受变量=函数名(参数)
但在自定义函数的脚本中所有函数都已function开头相当我我们c中的函数类型int void char等matlab中只有function,且所有函数都要以end结尾(相当于我们c中的break但是end不返回变量)
格式:function [返回变量] =函数名 (参数)
edn
3.对选定的列进项正向化处理
4.标准化处理
5.计算得分并归一化
代码参考:
主函数:
clear;clc
load data_water_quality.mat%导入的数据如果我们要引用的话记得前面添加load,但前提是你已经保存在和此代码同一文件夹中
%第一步判断指标是否需要正向化
[n,m] = size(X);%我们先获取我么导入数据的行行和列(n,m)
%对于有些指标不是极大型指标所以我们需要对其正向化
disp(['共有' num2str(n) '个评价对象' num2str(m) '个评价指标'])
judge = input(['这' num2str(m) '个指标是否需要正向化处理,需要请输入1,不需要请输出0:']);
%我们按评价指标的列排序做序号输入要正向化的指标对应的序号
Position = input('请输需要正向化处理的指标的所在的列,列如第1,2,3三列需要处理,那么你需要输入[1,2,3]: ');%[2,3,4]
%输入指标后我们position保存了要修改的指标序号
disp('请输入需要处理的这些列的指标类型(1:极小型,2:中间型,3:区间型)')
%我们type函数保存了对应指标的指标类型(如positon(1)是中间值那么type(i)就是3)
Type=input('列如:第二列是极小型,第二列是区间型,第三列是中间型,就输入 [1,3,2]:');%[2,1,3]
%我们自定义函数传参然后正向化
for i=1 : size(Position,2)
%X(:,Position(i))就是对我们X矩阵的列进行传参和接收
X(:,Position(i))=Positivization(X(:,Position(i)),Type(i),Position(i));
end
disp('正向化后的矩阵X=')
disp(X)
%end
%第二步:对正向化后的矩阵进行标准化
Z = X./repmat(sum(X.*X).^0.5,n,1)
disp('标准化矩阵Z = ')
disp(Z)
%第三步计算最大值的距离和最小值的距离,并算出得分
D_P = sum([(Z-repmat(max(Z),n,1)).^2],2).^0.5;
D_N = sum([(Z-repmat(min(Z),n,1)).^2],2).^0.5;
S = D_N ./ (D_P + D_N);
disp('最后得分为:')
stand_S = S/sum(S);
[sorted_S,index] = sort(stand_S,'descend')
正向化函数:
function [posit_x]=Positivization(x,type,i)
if type==1%及小型
disp(['第' num2str(i) '列是极小型,正在正向化'])
posit_x = Min2Max(x);
disp(['第' num2str(i) '列极小型正向化处理完成'])
disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~')
elseif type == 2%中间型
disp(['第' num2str(i) '列是中间型'])
best = input('请输入最佳的那个值:')
posit_x = Mid2Max(x,best);
disp(['第' num2str(i) '列中间型正向化处理完成'])
disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~')
elseif type == 3%区间型
disp(['第' num2str(i) '列是中间型,正在正向化'])
a = input('请输入区间的下界:');
b = input('请输入区间的上界:');
posit_x = Inter2Max(x,a,b);
disp(['第' num2str(i) '列中间型正向化处理完成'])
disp('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~')
else
disp('没有这种类型的指标,请检查Type向量中是否除了1,2,3之外的其他值')
end极小型正向化函数:
%极小型正向化:公式 max-每个元素
function [posit_x] = Min2Max(x)
posit_x=max(x)-x;
end中间型正向化函数:
%中间型正向化
%公式:先求M=max{|最大值-xi|的绝对值},xi=1-|最大值-x|/M
function [posit_x] = Mid2Max(x,best)
M = max(abs(x-best));
posit_x = 1 - abs(x-best) / M;
end区间型正向化函数:文章来源:https://www.toymoban.com/news/detail-568834.html
%区间型正向化
%公式:
%先求M=max{(a-最小值),(最大值-b)}
%xi:if xi<a,xi=1-(a-x)/M
%if xi>b,xi=1-(b-x)/M
%if a<=xi<=b,xi=1
function [posit_x] = Inter2Max(x,a,b)
r_x = size(x,1);
M = max([a-min(x),max(x)-b]);
posit_x =zeros(r_x,1);
for i=1 : r_x
if x(i) < a
posit_x(i) = 1-(a-x(i))/M;
elseif x(i)>b
posit_x(i) = 1-(x(i)-b)/M;
else
posit_x(i) = 1;
end
end
end
博主主要跟着清风数学建模的课程学习,其中里面的一些图片都来源于上课视频的截图。文章来源地址https://www.toymoban.com/news/detail-568834.html
到了这里,关于数学建模——TOPSIS法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!