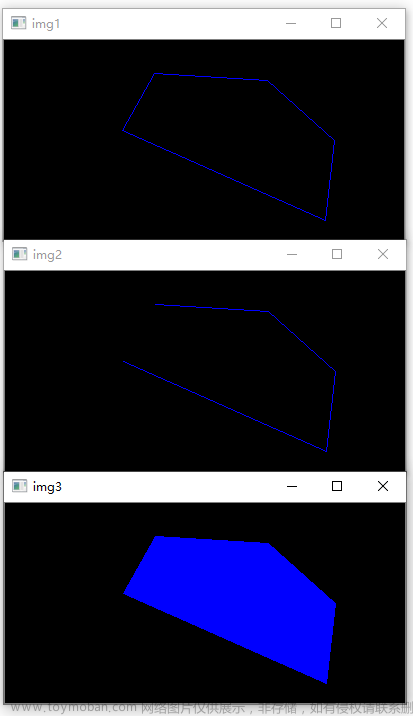
前言:用path画折线,2条线相交处导圆角
简介:为开发者提供工具类,方便对使用path画折线设置圆角。使用path画多边形,如三角形、矩形、平行四边形等,同时设置圆角。另外提供计算直线上某点坐标。
实现原理
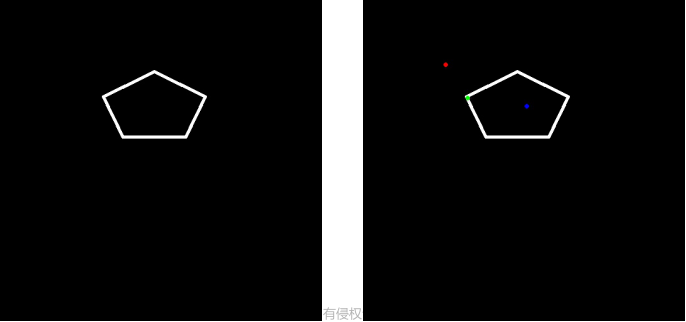
三个点,2条直线相交,给中间点连接处导圆角。设圆角半径为radius, 三个点分别为p2, p3,p1, 如下图所示:给p3点处导圆角。先求出导圆角处连接的2点p4、p5坐标,再用path连接p2和p4,然后通过p4、p3、p5绘制贝塞尔曲线连接p4、p5两个点,最后连接p5、p1两个点。
总结:计算圆角的起始和结束点,使用贝塞尔曲线绘制圆角。

API使用:
三角形导圆效果如下:
 导圆角之后
导圆角之后
调用api如下
int r = 22;//圆角尺寸
Path path = SimplePath.buildle()
.moveTo(50, 50, r, r)//起始点
.lineTo(200, 50, r, r)
.lineTo(200, 250, r, r)
.close()//结束,完成三角形
.build();矩形导圆角
Path path = SimplePath.buildle()
.addRect(50, 50, 200, 250, r)
.build();其它API使用:
获取线上点坐标 public static float[] getOnLinePointLocationEnd(float lenght, float x1, float y1, float x2, float y2)
示例:上述实现原理中,计算圆角起始坐标点p4. float[] p2f = SimplePath.getOnLinePointLocationEnd(r,x1,y1,x2,y2); Point p2 = new Point(p2f[0], p2f[1]); 其中r在这里是圆角半径,表示圆角起始点p4与中间点p2之间的距离。 画线并添加圆角 (绘制的线是起始点到圆角结束点的路径,并不包含到第三点路径) public static void lineToAndCorner(Path path, float startRadius, float endRadius, float x1, float y1, float x2, float y2, float x3, float y3)
示例:上述实现原理中,如果给p3点导圆角r.
path先要自行设置起始点p2, 然后
SimplePath.lineToAndCorner(path, r, r, p2.x, p2.y, p3.x, p3.y, p1.x,p1y);
绘制的线是 p2到p4,再到p5的路径, 不包含,p5到p1的路径。目标点是中间点p3.
备注:方法参数详情请查阅源码
源码:
package com.ttkx.deviceinfo.bkchart;
import android.graphics.Path;
import android.graphics.Rect;
import android.graphics.RectF;
import java.util.ArrayList;
import java.util.List;
public class SimplePath {
public static Buildle buildle() {
return new Buildle();
}
public static class Buildle {
private Path mPath;
private class P {
public float x;
public float y;
public float startRadius;
public float endRadius;
public boolean isStartPoint;//是否是起始点
public P(float x, float y) {
this.x = x;
this.y = y;
}
public P(float x, float y, float startRadiu, float endRadiu) {
this.x = x;
this.y = y;
this.startRadius = startRadiu;
this.endRadius = endRadiu;
}
}
private List<P> mList = new ArrayList<>();
public void moveTo(float x, float y) {
moveTo(x, y, 0, 0);
}
public Buildle setPath(Path path) {
mPath = path;
return this;
}
public Buildle moveTo(float x, float y, float startRadius, float endRadius) {
P p = new P(x, y, startRadius, endRadius);
p.isStartPoint = true;
mList.add(0, p);
return this;
}
public Buildle addRect(Rect rect, float r) {
return addRect(rect.left, rect.top, rect.right, rect.bottom, r);
}
public Buildle addRect(RectF rect, float r) {
return addRect(rect.left, rect.top, rect.right, rect.bottom, r);
}
public Buildle addRect(float left, float top, float right, float bottom, float r) {
moveTo(left, top, r, r);
lineTo(right, top, r, r);
lineTo(right, bottom, r, r);
lineTo(left, bottom, r, r);
close();
return this;
}
public Buildle lineTo(float x, float y) {
lineTo(x, y, 0, 0);
return this;
}
public Buildle lineTo(float x, float y, float startRadius, float endRadius) {
mList.add(new P(x, y, startRadius, endRadius));
return this;
}
public Buildle close() {
if (mList.size() >= 1) {
mList.add(mList.get(0));
}
return this;
}
public Path build() {
Path path = mPath;
if (path == null) {
path = new Path();
}
for (int i = 0; i < mList.size(); i++) {
P p = mList.get(i);
float x = p.x;
float y = p.y;
if (i == 0) {
if (p.isStartPoint) {
if (hasCorner(p)) {
P p1 = mList.get(i + 1);
P p2 = p;
float[] onePoint = getOnLinePointLocationEnd(p.startRadius, p1.x, p1.y, p2.x, p2.y);
path.moveTo(onePoint[0], onePoint[1]);
} else {
path.moveTo(x, y);
}
} else {
path.lineTo(x, y);
}
} else if (i == mList.size() - 1) {
//最后一个点
P p0 = mList.get(0);
if (p.x == p0.x && p.y == p0.y && hasCorner(p0)) {
P p1 = mList.get(i - 1);
P p2 = p0;
P p3 = mList.get(1);
lineToAndCorner(path, p2.startRadius, p2.endRadius, p1.x, p1.y, p2.x, p2.y, p3.x, p3.y);
} else {
path.lineTo(p.x, p.y);
}
} else {
if (hasCorner(p)) {
P p1 = mList.get(i - 1);
P p2 = p;
P p3 = mList.get(i + 1);
lineToAndCorner(path, p2.startRadius, p2.endRadius, p1.x, p1.y, p2.x, p2.y, p3.x, p3.y);
} else {
path.lineTo(x, y);
}
}
}
return path;
}
private boolean hasCorner(P p) {
return p.endRadius > 0 && p.startRadius > 0;
}
}
/**
* 画线并添加圆点 (绘制的线是起始点到圆角结束点的路径,并不包含到p3点路径)
*
* @param path
* @param startRadius 起始圆角半径
* @param endRadius 结束圆角半径
* @param x1 起始点
* @param y1
* @param x2 中间点
* @param y2
* @param x3 结束点
* @param y3
*/
public static void lineToAndCorner(Path path, float startRadius, float endRadius, float x1, float y1, float x2, float y2, float x3, float y3) {
float[] onePoint = getOnLinePointLocationEnd(startRadius, x1, y1, x2, y2);
path.lineTo(onePoint[0], onePoint[1]);
float[] twoPoint = getOnLinePointLocationStart(endRadius, x2, y2, x3, y3);
//绘制圆角
path.cubicTo(onePoint[0], onePoint[1], x2, y2, twoPoint[0], twoPoint[1]);
}
/**
* 获取线上点坐标
*
* @param lenght 线上点距离起始点(x1,y1)长度
* @param x1 起始点x坐标
* @param y1 起始点y坐标
* @param x2 结束点x坐标
* @param y2 结束点y坐标
* @return
*/
public static float[] getOnLinePointLocationStart(float lenght, float x1, float y1, float x2, float y2) {
double degree = getDegree(x1, y1, x2, y2);
double dx = getRightSideFromDegree(degree, lenght);
double dy = getLeftSideFromDegree(degree, lenght);
double v2 = x1 + dx;
double v3 = y1 + dy;
return new float[]{(float) v2, (float) v3};
}
/**
* 获取线上点坐标
*
* @param lenght 线上点距离结束点(x2,y2)长度
* @param x1 起始点x坐标
* @param y1 起始点y坐标
* @param x2 结束点x坐标
* @param y2 结束点y坐标
* @return
*/
public static float[] getOnLinePointLocationEnd(float lenght, float x1, float y1, float x2, float y2) {
double degree = MathHelper.getDegree(x1, y1, x2, y2);
double dx = MathHelper.getRightSideFromDegree(degree, lenght);
double dy = MathHelper.getLeftSideFromDegree(degree, lenght);
double v2 = x2 - dx;
double v3 = y2 - dy;
return new float[]{(float) v2, (float) v3};
}
//两点间的角度
private static double getDegree(float sx, float sy, float tx, float ty) {
float nX = tx - sx;
float nY = ty - sy;
double angrad = 0d, angel = 0d, tpi = 0d;
float tan = 0.0f;
if (Float.compare(nX, 0.0f) != 0) {
tan = Math.abs(nY / nX);
angel = Math.atan(tan);
if (Float.compare(nX, 0.0f) == 1) {
if (Float.compare(nY, 0.0f) == 1 || Float.compare(nY, 0.0f) == 0) {
angrad = angel;
} else {
angrad = 2 * Math.PI - angel;
}
} else {
if (Float.compare(nY, 0.0f) == 1 || Float.compare(nY, 0.0f) == 0) {
angrad = Math.PI - angel;
} else {
angrad = Math.PI + angel;
}
}
} else {
tpi = Math.PI / 2;
if (Float.compare(nY, 0.0f) == 1) {
angrad = tpi;
} else {
angrad = -1 * tpi;
}
}
return Math.toDegrees(angrad);
}
/**
* 直角三角形 根据角度和斜边求直角边
*
* @param degree 角度
* @param width 斜边
* @return 直角边长
*/
private static double getRightSideFromDegree(double degree, double width) {
double cos = Math.cos(Math.toRadians(degree));
return width * cos;
}
private static double getLeftSideFromDegree(double degree, double width) {
double sin = Math.sin(Math.toRadians(degree));
return width * sin;
}
}
实践:绘制带箭头的提示框背景
第一步:先绘制带圆角的三角形。
三角形只有一个角导圆角
int r = 10;//圆角尺寸
int ph = 30;//箭头离左侧距离
int arrowsHeight = 35;//箭头高度
Point p1 = new Point(ph, arrowsHeight);
Point p2 = new Point(ph + arrowsHeight * 2, arrowsHeight);
Point p3 = new Point(ph + arrowsHeight, 0);
Path path = SimplePath.buildle()
.setPath(new Path())//设置path (可以设置也可以不设置, 若不设置工具类自己创建一个path对象)
.moveTo(p1.x, p1.y)//起始点
.lineTo(p2.x, p2.y)
.lineTo(p3.x, p3.y, r, r)
.close()
.build();效果如下:
第二步:添加圆角矩形
int rectRadius = 30; path.addRoundRect(new RectF(0,arrowsHeight, getBounds().right, getBounds().bottom), rectRadius, rectRadius ,Path.Direction.CW);

第三步:创建自定义Drawable, 将path绘制出来,再将drawable设置为textView 背景, 最后给textView设置padding即可。文章来源:https://www.toymoban.com/news/detail-569107.html
效果如下:文章来源地址https://www.toymoban.com/news/detail-569107.html
到了这里,关于Android 多边形导圆角(Path画折线导圆角)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!