目录
一、向量点乘&叉乘
1.点乘
1.1 公式
1.2 几何意义
2.叉乘
2.1 公式
2.2 几何意义
二、矩阵点乘&叉乘
1.矩阵
2.矩阵的点乘
3.矩阵的叉乘
三、矩阵旋转
四、齐次坐标
一、向量点乘&叉乘
1.点乘
又称内积,结果是个标量,
1.1 公式
向量a与向量b点乘的计算公式有两个:
- a·b=(x1, y1, z1)·(x2, y2, z2)=x1×x2+y1×y2+z1×z2;
- a·b=‖a‖×‖b‖×cosβ。
1.2 几何意义
如下图所示,当a和b两个向量点乘得到的结果为正数时,两者的方向比较一致,并且这个正数越大,a和b两个向量的方向越一致,直至得到的正数最大时,两者的方向完全相同。当a和b两个向量点积得到的结果为负数时,a和b两个向量的方向则相反,得到的负值越小,a和b的方向相反的程度越厉害,当负数最小时,两者方向完全相反。

点乘除了可以判断两个向量的方向外,还可以用来计算β的角度(从而计算是否平行或者垂直),即:β=arcos((a·b)/(|a|×|b|))。在Unity中为:β=Mathf.Acos(Vector3.Dot(a, b)/(a.magnitude×b.magnitude))
点乘还可以用来计算向量在某个方向上的投影长度,从而实现向量的投影变换。
2.叉乘
又称外积、向量积。与Vector3点积一样,Vector3的叉乘也是向量与向量之间的计算公式,不同的是,叉乘的结果不再是一个数值,而是一个同样维度的向量。
2.1 公式
c=a×b=(a1, a2, a3)×(b1, b2, b3)=(a2×b3-a3×b3, a3×b1-a1×b3, a1×b2-a2×b1)
式中,两个向量a、b叉乘后,得到与a、b向量形成的平面垂直的向量c。
c的长度又可以用另一个公式来表示,即a×b的长度等于向量的大小与向量的夹角sin值的积:|c|=|a×b|=|a|×|b|×sinβ。
- 当c的长度为0时,a和b是两个相互平行的矢量,当a和b的叉乘的模等于a的模乘以b的模时,a和b是两个互相垂直的向量。
- a向量和b向量叉乘的模就是a向量和b向量形成的四边形面积。

2.2 几何意义
- 得到与两向量形成的平面垂直的向量;
- 判断两向量是否平行或垂直;
- 向量叉乘后的模就是四边形的面积。
二、矩阵点乘&叉乘
1.矩阵
- 对角矩阵:即只有行号和列号相同的位置有数字,其他位置都为0的方阵矩阵
- 单位矩阵:即行号和列号相同的对角线上的数字都为1,其他位置都为0的方阵矩阵
- 转置矩阵:就是把矩阵沿着对角线翻转一下,由于我们常用的是“方阵”矩阵,所以转置矩阵后,方阵矩阵还是同样的大小,只是将对角线两侧的数字进行了对调。
2.矩阵的点乘
数字和矩阵相乘,直接代入矩阵中的所有变量即可,这种标量的乘法其实就是扩大矩阵中的所有数值。结果是个矩阵。
矩阵与矩阵点乘,英文hadamard product,因此又称哈达码积。要求相乘的两个矩阵A和B大小完全相同,即A、B大小都为M*N。结果可能是矩阵、列向量、行向量。
3.矩阵的叉乘
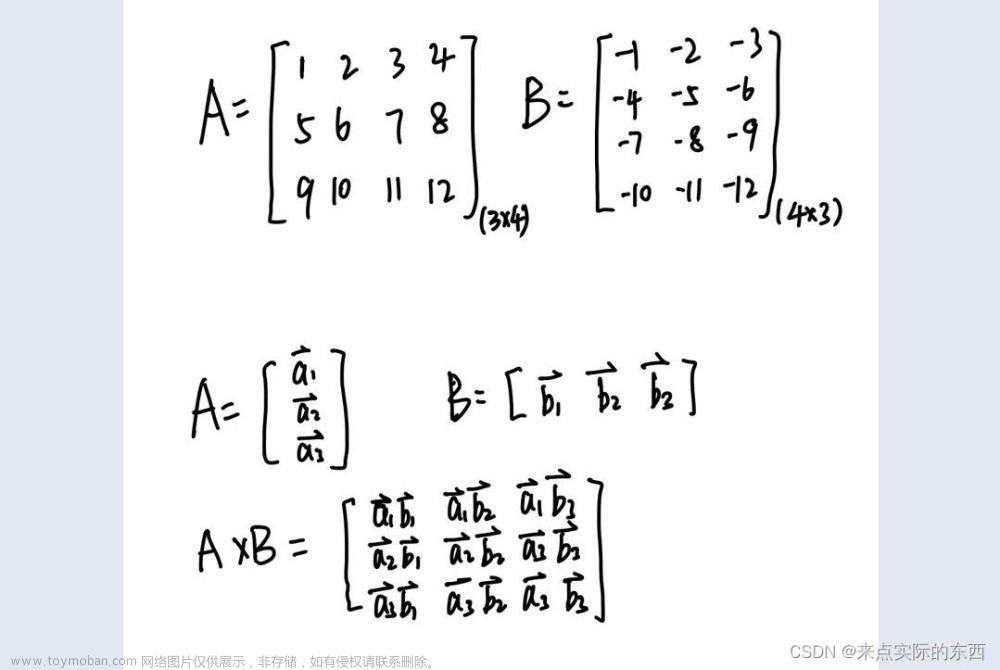
一般而言,矩阵相乘表示的是矩阵的叉乘,叉乘的结果是个矩阵。矩阵相乘(A矩阵×B矩阵)需要一些附加条件,条件是矩阵A的列数必须与矩阵B的行数相等,否则无法相乘,或者说相乘是无意义的。
矩阵相乘后得到的矩阵,其中每个位置Cij(即C矩阵的第i行第j列)都是A矩阵的第i行向量与B矩阵的第j列向量点乘的计算结果。
当一个矩阵与某个矩阵相乘等于单位矩阵时,这“某个”矩阵就为该矩阵的“逆矩阵”。如果一个矩阵有逆矩阵,则称这个矩阵为可逆矩阵;相反,如果这个矩阵没有逆矩阵,那么就称这个矩阵为不可逆矩阵。
三、矩阵旋转
我们可以说矩阵是由标准矩阵旋转并缩放而来的,这是矩阵的几何解释。对于标准矩阵来说,旋转缩放后形成另一个矩阵,这个结果矩阵就是我们计算的“变换矩阵”。对于任何一个向量来说,乘以“变换矩阵”就能得到我们所要表达的旋转和缩放值。
一个矩阵想要旋转β°,那么旋转矩阵的第一行是[cosβ,sinβ],第二行是[-sinβ,cosβ],它们分别表达了标准向量(1,0)和(0,1)旋转β°后的向量。如下图所示。
任何向量乘以这个旋转矩阵都会在标准坐标系中以标准轴为基准旋转β°。

四、齐次坐标
齐次坐标就是将一个原本是n维的向量用一个n+1维的向量来表示,例如三维向量用四维向量来表示,即Vector3变为Vector4,除x、y、z外,又多了一个w,齐次矩阵也是同样的道理,n维表达不了的事情可用n+1维来表达,3×3矩阵表达不了的事情可以用4×4来表达
在欧几里得几何空间里,两条平行线永远都不会相交(引自《齐次坐标》)。但是在投影空间中,在无限远处两条平行线看起来会相交于一点。
由August Ferdinand Möbius提出的齐次坐标(Homogeneous Coordinates)让我们能够在投影空间里对图像进行几何处理,齐次坐标用N+1个分量来描述N维坐标。比如,2D齐次坐标是在笛卡儿坐标(X,Y)的基础上增加一个新分量w,变成(x,y,w),其中笛卡儿坐标系中的大X、Y与齐次坐标中的小x、y有如下对应关系:X=x/wY=y/w。笛卡儿坐标中的点(1,2)在齐次坐标中就是(1,2,1)。如果这点移动到无限远(∞,∞)处,在齐次坐标中就是(1,2,0),这样就避免了用没意义的“∞”来描述无限远处的点。
点(1,2,3)、(2,4,6)和(4,8,12)对应笛卡儿坐标中的同一点(1/3,2/3)。任意数量积的(1a,2a,3a)始终对应笛卡儿坐标中的同一点(1/3,2/3)。因此这些点是“齐次”的,因为它们始终对应笛卡儿坐标中的同一点。换句话说,齐次坐标描述的是缩放不变性(Scale Invariant)。文章来源:https://www.toymoban.com/news/detail-572438.html
矩阵乘法很强大,可以表达旋转、缩放、投影、镜像、切变,但无法表达平移(由于矩阵乘法的性质,任何矩阵乘以零向量都是零,因此零向量无法平移),怎么办?齐次矩阵恰好可以满足我们的需求,齐次矩阵在原来的维度上增加了一个维度,用多出来的那个维度来表达平移操作。文章来源地址https://www.toymoban.com/news/detail-572438.html
到了这里,关于Unity | 向量、矩阵、齐次坐标的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!