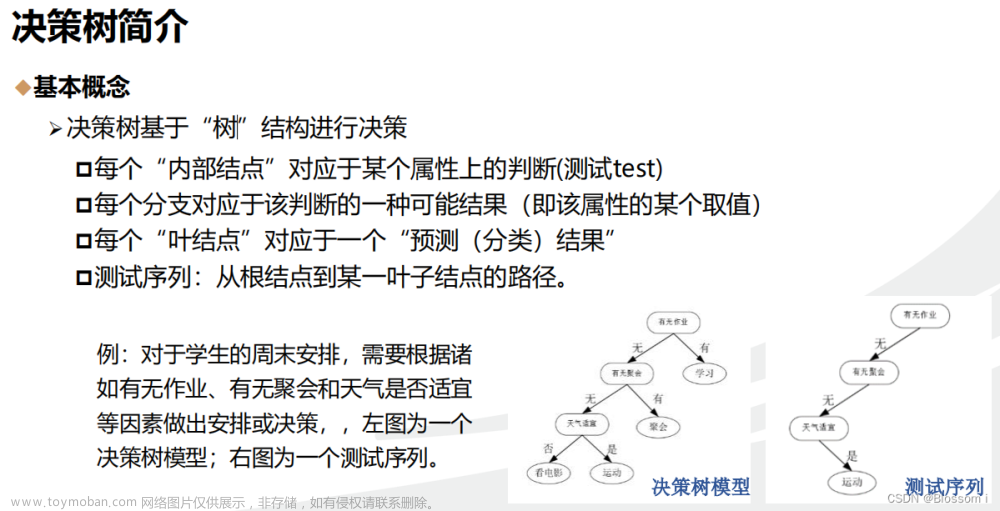
决策树是机器学习算法的一种,它主要对给定数据集合根据相关属性生成一个类似树结构的一种决策机制。
生成树结构,其实可以很随便,只要根据特征值的分支做分叉,把所有的特征遍历完成,这棵树就是一颗决策树。但是要生成一个最优决策树,我们需要选择合适的根节点。
有一种选择根节点的算法是ID3算法,它根据信息增益来选择特征作为根节点。
信息熵的定义:香浓提出熵的概念,表示随机变量不确定度的衡量。
从描述看来,不确定度,这里其实就隐含着概率的问题,而熵的计算公式,正是用来计算这个概率和。设X是一个取值有限的离散随机变量,其概率分布为:
,则随机变量X的熵定义为:
这个公式看着有些奇怪,我们计算信息熵,应该是一个概率和,最终是大于0的数字,这个公式里面怎么有一个减号-,其实我们知道这里概率是一个0-1之间的数字,最大不超过1,而对数函数在0-1范围,结果就是负数,如下所示:

所以,这里的减号正好将负数变为正数,最后结果就大于0并不是负数。
熵的结果,只能说明信息不确定度。熵越大,信息不确定度越大,样本分布越分散,熵越小,不确定度越小,样本更集中。
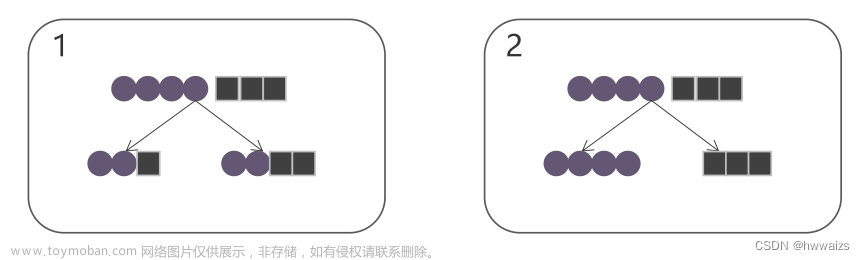
比如我们通过如下示例来看看样本分布情况对应的熵。

上图中,我们假定
1、所有样本都是一个颜色,那么熵最后计算的结果是0。
2、样本中混入一个红色,那么最后计算结果是0.811,
3、样本中红色,蓝色都是一样的,他们概率都是50%,那么熵的结果就是1。
熵的结果与样本结果有关,与特征值没有关系。
信息增益的定义:字面意思来说,它是一个差值,信息增益的差值,而这个信息增益差,需要和特征和特征值挂钩,这里就产生一个权重,特征值对应样本占总体样本的比例。它又是另一个层面的概率。
定义如下:假定特征a有如下可能取值,也就是分支:{ },如果使用a来进行划分,就会产生v个分支。其中,第v个分支,包含了样本X中,取值为的样本,记为,我们可以根据前面信息熵的定义计算的熵。考虑有v个分支样本量不相同,假定每个分支的权重,如是,就可以计算出使用特征a来划分数据集X的信息增益:
信息增益表示的意思,使用特征a来划分对整个样本纯度提升的大小,提升越大,这个特征就越好,所以在构建决策树的时候,我们优先选择这个特征。选择完当前特征,我们就应该去掉该特征 ,继续使用剩下的特征来进行新的划分,直到所有特征划分完成。
下面根据一个具体的示例,我们来看看如何选择一个好的根节点。
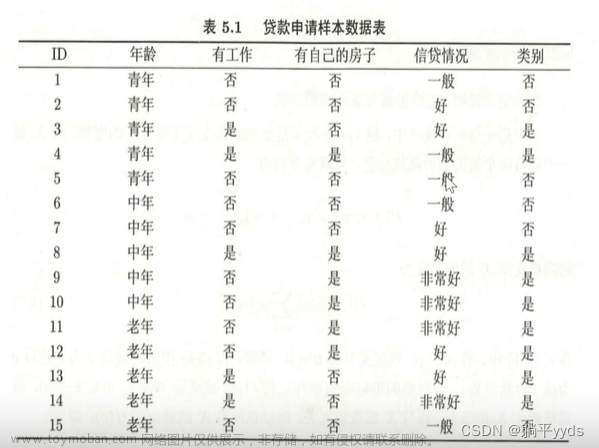
如下所示,是一个银行根据贷款对象的年龄,工作,房产,贷款情况决定是否给与贷款的样本:

第一个表格是样本情况,第二个表格是根据第一个表格进行的样本统计。
接着我们使用上面的信息熵和信息增益来计算相关数据。
总体信息熵,这个只需要通过样本中是、否的概率来计算即可。
Ent(X) = = 0.971
信息增益:
Gain(X, 年龄) =
Gain(X, 工作) =
Gain(X, 房产) =
Gain(X, 贷款情况) =
以上计算过程通过代码演示如下:
from math import log2
def create_datasets():
datasets = [[0, 0, 0, 0, 'no'],
[0, 0, 0, 1, 'no'],
[0, 1, 0, 1, 'yes'],
[0, 1, 1, 0, 'yes'],
[0, 0, 0, 0, 'no'],
[1, 0, 0, 0, 'no'],
[1, 0, 0, 1, 'no'],
[1, 1, 1, 1, 'yes'],
[1, 0, 1, 2, 'yes'],
[1, 0, 1, 2, 'yes'],
[2, 0, 1, 2, 'yes'],
[2, 0, 1, 1, 'yes'],
[2, 1, 0, 1, 'yes'],
[2, 1, 0, 2, 'yes'],
[2, 0, 0, 0, 'no']]
labels = ['F-Age', 'F-Work', 'F-House', 'F-Loan', 'Target']
return datasets, labels
def calc_shannon_entropy(datasets):
data_len = len(datasets)
label_count = {}
for i in range(data_len):
label = datasets[i][-1]
if label not in label_count:
label_count[label] = 0
label_count[label] += 1
entropy = -sum([(p / data_len) * log2(p / data_len) for p in label_count.values()])
return entropy
def cal_condition_entropy(datasets, axis=0):
data_len = len(datasets)
feature_sets = {}
for i in range(data_len):
feature = datasets[i][axis]
if feature not in feature_sets:
feature_sets[feature] = []
feature_sets[feature].append(datasets[i])
condition_entropy = sum([(len(p) / data_len) * calc_shannon_entropy(p) for p in feature_sets.values()])
return condition_entropy
def info_gain(entropy, condition_entropy):
return entropy - condition_entropy
def info_gain_train(datasets, labels):
count = len(datasets[0]) - 1
entropy = calc_shannon_entropy(datasets)
best_feature = []
for i in range(count):
info_gain_i = info_gain(entropy, cal_condition_entropy(datasets, axis=i))
best_feature.append((i, info_gain_i))
print('feature : {},info_gain : {:.3f}'.format(labels[i], info_gain_i))
best_ = max(best_feature, key=lambda x: x[-1])
return labels[best_[0]]
if __name__ == '__main__':
datasets, labels = create_datasets()
ent = calc_shannon_entropy(datasets)
print('entropy : {}'.format(ent))
feature = info_gain_train(datasets, labels)
print('best feature : {}'.format(feature))
运行结果:
entropy : 0.9709505944546686
feature : F-Age,info_gain : 0.083
feature : F-Work,info_gain : 0.324
feature : F-House,info_gain : 0.420
feature : F-Loan,info_gain : 0.363
best feature : F-House 文章来源:https://www.toymoban.com/news/detail-578651.html
在决策树生成过程中,上面的部分只是一个开端,求出了最合适的根节点,后续还需要根据其他特征继续递归求解新的合适的节点。文章来源地址https://www.toymoban.com/news/detail-578651.html
到了这里,关于信息熵与信息增益在决策树生成中的使用的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!