目录
一、说明
二、仿射映射
2.1 直线上的仿射映射定义
2.2 平面间的仿射映射定义
三、仿射不变性性质
四、平面到自身的透视仿射
五、透视仿射和透视映射的关系
5.1 射影透视变换和仿射的关系
5.2 仿射函数和线性函数的区别
一、说明
简单来说,“仿射变换”就是:“线性变换”+“平移”,但这是在笛卡尔坐标下的表现,然而在射影几何中,其中有更合乎逻辑的解释。本文讲仿射映射的定义,以及仿射不变性的特点。
二、仿射映射
2.1 直线上的仿射映射定义

多重仿射映射

2.2 平面间的仿射映射定义

三、仿射不变性性质
- 定理 1 二直线间的平行性是仿射不变性.
- 定理 2 共线三点的简比是仿射不变量.
定义 设 A, B, C 为共线三点,这三点的简比( A B C)定义为 下述有向线段的比:
( A B C) = A C:B C.映射后不变
( C 在线段 A B 上时,简比( A B C) < 0,在 A B 的延长线上时,( A B C) > 0. )
- 定理 3 两条平行线段之比是仿射不变量.
- 定理 4 一直线上任两线段之比是仿射不变量
-
定理 5 在仿射变换下,任何一对对应三角形面积之比等于常数.换句话说,任意两个三角形面积之比是仿射不变量.
-
系1 在仿射变换下,任何一对对应多边形面积之比等于常 数.换句话说,任意两个多边形面积之比是仿射不变量。
-
系 2 在仿射变换下,任意两条封闭凸曲线所围成的面积之比是仿射不变量.
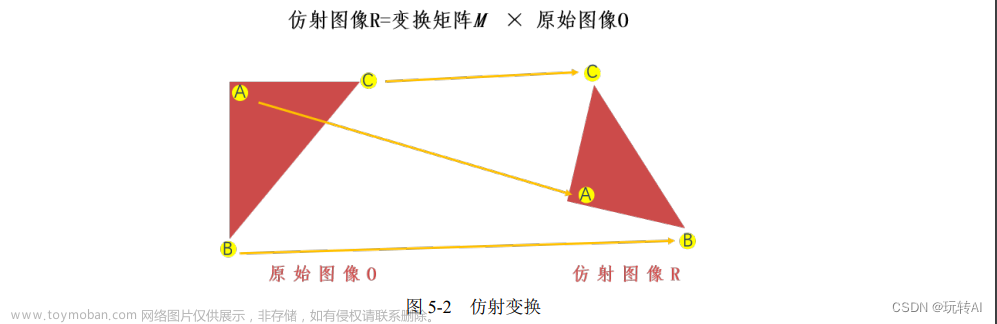
四、平面到自身的透视仿射
这个很重要,图像处理的仿射变换就是指这种。

五、透视仿射和透视映射的关系
5.1 射影透视变换和仿射的关系
仿射变换是任何保持共线性(即,最初位于一条线上的所有点在变换后仍位于一条线上)和距离比(例如,线段的中点在变换后仍为中点)的任何变换。从这个意义上说,仿射表示一类特殊的射影变换,它不会将任何物体从仿射空间 R^3 移动到无穷远平面或相反。仿射变换也称为亲和性。
几何收缩、膨胀、膨胀、反射、旋转、剪切、相似变换、螺旋相似和平移都是仿射变换,它们的组合也是如此。通常,仿射变换是旋转、平移、膨胀和剪切的组合。
虽然仿射变换保留直线的比例,但不一定保留角度或长度。任何三角形都可以通过仿射变换变成任何其他三角形,因此所有三角形都是仿射的,从这个意义上说,仿射是全等和相似的推广。
结合旋转和扩展的一个特殊例子是旋转放大变换
5.2 仿射函数和线性函数的区别
仿射函数即由由1阶多项式构成的函数,一般形式为 f (x) = A x + b,这里,A 是一个 m×k 矩阵,x 是一个 k 向量,b是一个m向量,实际上反映了一种从 k 维到 m 维的空间映射关系。
设f是一个矢性(值)函数,若它可以表示为f(x1,x2,…,xn)=A1x1+A2x2+…+Anxn+b,其中Ai可以是标量,也可以是矩阵,则称f是仿射函数。文章来源:https://www.toymoban.com/news/detail-581893.html
其中的特例是,标性(值)函数f(x)=ax+b,其中a、x、b都是标量。此时严格讲,只有b=0时,仿射函数才可以叫“线性函数”(“正比例”关系)。文章来源地址https://www.toymoban.com/news/detail-581893.html
到了这里,关于【射影几何08】仿射映射的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!