1. ELGamal离散对数密码体制
1. 公钥生成
① Alice首先构造一条椭圆曲线E,在曲线上选择一点G作为生成元,并求G的阶为n,要求n必须为质数。此时构成了一个循环群<G>.
② Alice选择一个私钥k (k < n),生成公钥 Q = kG
③ Alice将公钥组E、Q、G发送给Bob
2. 加密过程
① Bob收到信息后,将明文编码为M,M为曲线上一点,并选择一个随机数r(r < n, n为G的阶)
② Bob计算点C1与C2即两段密文,计算方法如下:
- C1 = M + rQ
- C2 = rG
③Bob把C1和C2发给Alice
3. 解密过程
① Alice收到密文后,为了获得M,只需要Cipher1 - k · Cipher2,因为
C1 - k*2 = M + rQ - krG = M + rkG - krG = M② 将M解码即可
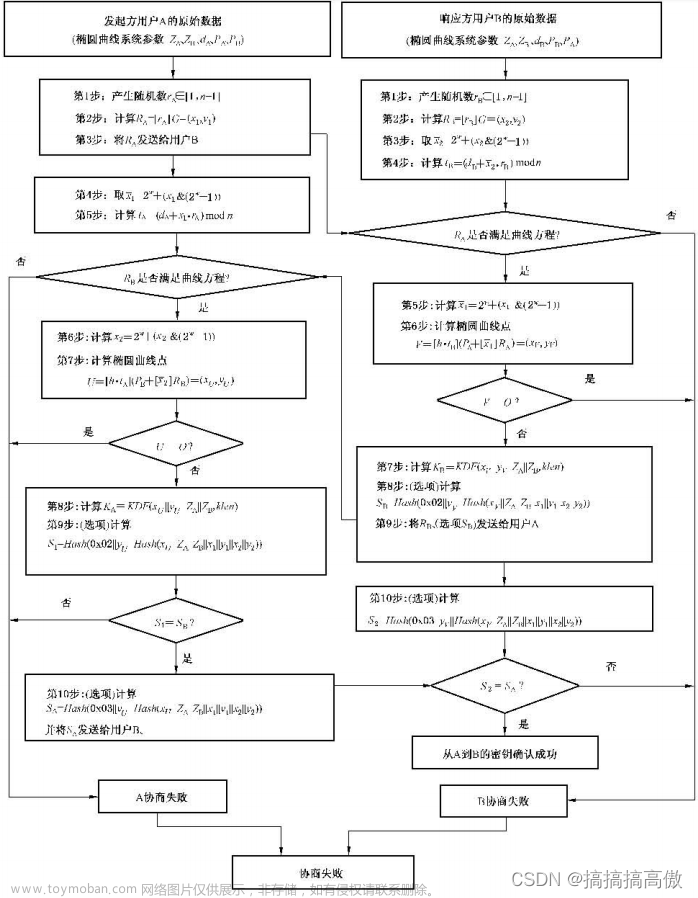
2.SM2加密流程
备注:
1.密钥派生函数(KDF):通过作用于共享秘密和双方都知道的其他参数,产生一个或者多个共享秘密的密钥的函数.密钥派生函数需要调用杂凑算法,设密码杂凑算法为H_v( ),其输出的是长度恰为v比特的杂凑值;
密钥派生函数KDF(Z,klen)

2. h为余因子 ,h=#E(Fq)/n,n为基点G的阶,#E(Fq)为E(Fq)上点的数目,称为椭圆曲线E(Fq)的阶.
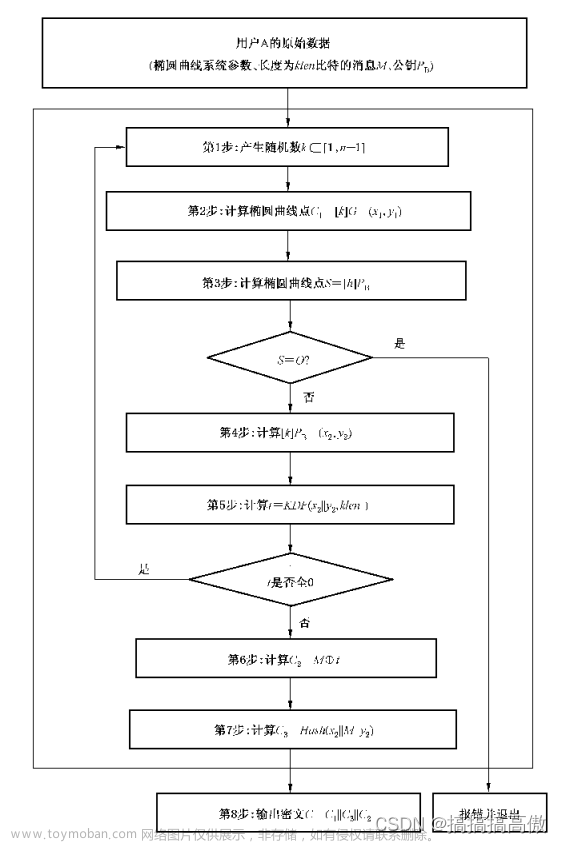
1. 加密算法流程
① 用随机数发生器产生随机数k (1<k<n-1)
② 计算椭圆曲线点C1=[k]G=(x1,y1),并将其转换为比特串(A的私钥生成公钥)
③ 计算椭圆曲线点S=[h]Pb,若S是无穷远点,则报错并退出 h为n的余因子
④ 计算椭圆曲线点[k]Pb=(x2,y2),并将其转换为比特串(A的私钥乘B的公钥)
⑤ 计算t=KDF(x2||y2,klen),若t为全0比特串,则返回①; KDF为密钥派生函数
⑥ 计算C2=M⊕t
⑦ 计算C3=Hash(x2||M||y2)
⑧ 输出密文C=C1||C3||C2
2. 解密算法的流程
① 从C中取出比特串C1,将其转换为椭圆曲线上的点,验证C1是否满足椭圆曲线方程
② 计算椭圆曲线点S=[h]Pb,若S是无穷远点,则报错并退出
③ 计算[db]C1=(x2,y2),并将其转换为比特串 db B的公钥
④ 计算t=KDF(x2||y2,klen),若t为全0比特串,则返回(一) KDF为密钥派生函数
⑤ 从C中取出比特串C2,计算M=C2⊕t
⑥ 计算u=Hash(x2||M||y2),从C中取出比特串C3,若u不等于C3,则报错并退出文章来源:https://www.toymoban.com/news/detail-581977.html
⑦ 输出明文M文章来源地址https://www.toymoban.com/news/detail-581977.html
到了这里,关于椭圆曲线密码(SM2)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!