Python 数据正向化 (数学建模)-Toy模板网

这篇具有很好参考价值的文章主要介绍了Python 数据正向化 (数学建模)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

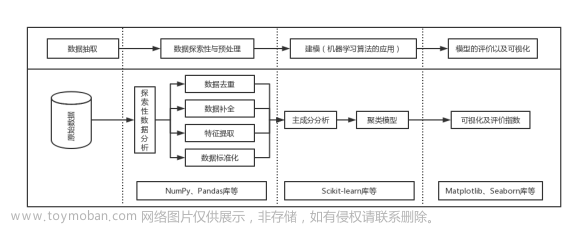
正向化：指将指标转化为越大越好，例如求最小值，乘以符号转化为求最大值

注：x为numpy数组

极小型指标正向化：
中间型指标正向化（例如PH值需要越接近7越好,xbest=7.0，转化为越大越好）:
区间型指标正向化

# RegularizeData.py
# 数据正向化
# 指标名称          指标特点
# 极大型(效益型)指标  越大（多)越好
# 极小型（成本型)指标 越小(少）越好
# 中间型指标         越接近某个值越好
# 区间型指标         落在某个区间最好
import numpy as np


# method = 0, 1, 2
# 0: 极小型（成本型)指标
# 1: 中间型指标        越接近某个值越好，传入best_value
# 2: 区间型指标      落在某个区间最好，传入left_bound, right_bound
def regularize_column_vector(data: np.ndarray, best_value: float = None,
                             left_bound: float = None,
                             right_bound: float = None,
                             method: int = 0) -> np.ndarray:
    if len(data.shape) != 1:
        raise ValueError("data must be a row vector")
        return None
    if method == 0:
        return data.max() - data
    elif method == 1:
        dis = max(data.max() - best_value, best_value - data.min())
        return 1 - ((data - best_value).__abs__()/dis)
    elif method == 2:
        dis = max(data.max() - right_bound, left_bound - data.min())
        for i in range(data.shape[0]):
            if data[i] > right_bound:
                data[i] = 1 - ((data[i] - right_bound) / dis)
            elif data[i] < left_bound:
                data[i] = 1 - ((left_bound - data[i]) / dis)
            else:
                data[i] = 1
        return data

使用示例

if __name__ == '__main__':
    print(RegularizeData.regularize_column_vector(np.array([1, 2, 3, 4, 5]),
                                             method=1, best_value=3.0))

输出结果