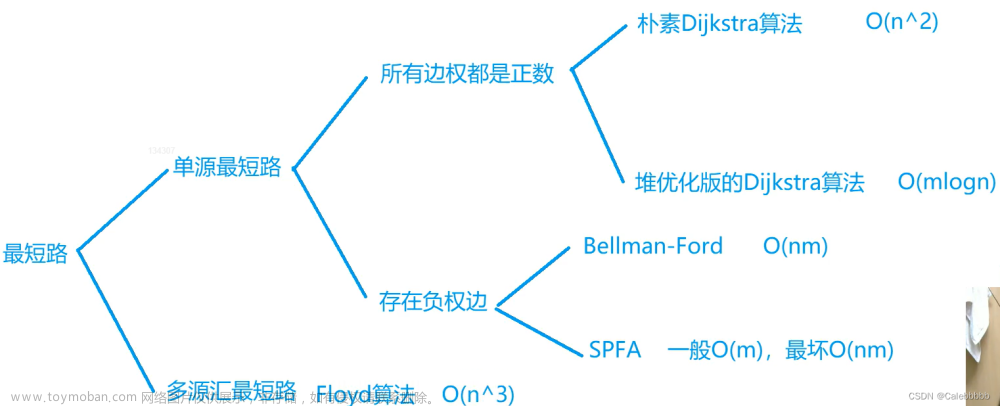
bellman-ford算法的思想 :
若有向图有n个点,m条边 。 扫描所有边,对每条边进行一次松弛(即对a,b为端点 , 权重为w的边,dist[b] = min(dist[a] , dist[a] + w )) 重复此流程(最多重复n次)直到没有更新操作发生
例题1 bellmanford板子
给你一张 n 个顶点 m 条边的有向简单图,顶点编号从 1 到 n,每条边都有一个边权,边权为非负整数。
现在有 k 组询问,每组询问读入两个整数 x,y 请求出从 x 号点到 y 号点的最短路的长度。如果不存在从 x 号点到 y 号点的路径,请输出 -1。
输入格式
第一行三个整数 n,m,k表示图的顶点数、边数和询问次数。
接下来 m𝑚 行,每行三个整数 x,y,z表示 x𝑥 号点到 y 号点有一条边权为 z 的有向边。
接下来 k 行,每行两个整数 x,y表示一组询问。
输出格式
输出共 k 行,每行一个数表示一组询问的答案。
样例输入
3 3 2
1 2 3
2 3 2
3 2 1
1 3
3 1
样例输出5
-1
数据规模对于所有数据,保证 2≤n≤5000,0≤m≤10000,1≤k≤5,1≤x,y≤n,1≤z≤100002≤n≤5000,0≤m≤10000,1≤k≤5,1≤x,y≤n,1≤z≤10000。
我们可以发现K非常小,那么我们可以对每次询问都做一次bellman - ford算法,求出dist[y]
代码
# include<bits/stdc++.h>
using namespace std;
const int M = 1e4+10,N = 5010; //N根据点的数据范围定的 M根据边
struct edge
{
int x,y,w; //起点,终点,边权
}edge[M]; //建立一个数组装所有边
int dist[N]; //每个点距离初始点的距离
int main()
{
int n,m,k;cin>>n>>m>>k;
for(int i=0;i<m;i++)
{
cin>>edge[i].x>>edge[i].y>>edge[i].w;
}
while(k--) //进行k次bellman - ford算法
{
int x,y;scanf("%d%d",&x,&y);
memset(dist,0x3f,sizeof(dist)); //每次都要先更新dist数组,将起点的dist设置为0
dist[x] = 0;
while(1)
{
bool flag = false; //只要dist更新,flag就会被置为true
for(int i=0;i<m;i++)
{
int a = edge[i].x,b = edge[i].y,d = edge[i].w;
if(dist[b] > dist[a] + d) //遍历每条边进行松弛操作
{
flag = true;
dist[b] = dist[a] + d;
}
}
if(!flag) break; //只要不在更新,则bellman-ford算法结束
}
if(dist[y] > 0x3f3f3f3f/2) cout<<"-1"<<endl; //因为每条边都会进行松弛所以即使走不到dist的值也不再是0x3f3f3f3f
else cout<<dist[y]<<endl;
}
return 0;
}
例题2
小蜗要在城市中租房子,他想要找到一处合适的住址,使得住址到商场、工作地点、医院的距离和最小。城市可以抽象为一张 n 个点 m 条边的无向简单图,顶点编号从 1 到 n,每条边都有一个边权,边权为非负整数。
输入格式
第一行两个整数 n,m,表示图的顶点数和边数。
接下来 m𝑚 行,每行三个整数 x,y,z表示 x 号点和 y 号点之间有一条边权为 z 的边。
接下来一行三个整数 a,b,c分别表示商场、工作地点、医院所在的顶点的编号。
输出格式
你需要寻找一个合适的住址(住址必须为 n 个顶点中的某个点,这个点可以和 a,b,c 重合),并输出一行一个整数表示住址到商场、工作地点、医院的最小距离和。
样例输入
4 3
1 2 1
2 3 1
3 4 1
1 2 4
样例输出3
数据规模对于所有数据,保证 3≤n≤5000,0≤m≤10000,1≤x,y,a,b,c≤n,1≤z≤10000 保证整张图连通并且 a,b,c两两不同。
我们可以先想一个最无脑的做法 :
遍历n个点,对每个点做一遍bellman-ford,每次算出这个点到a,b,c的和的最小值并记录,最后看最小值对应的是哪个点,复杂度是o(n²m) 如果这样子最差需要操作1e10次,会超时。
那我们不妨先对a,b,c各做一次bellman-ford,然后遍历n个点找到距离和的最小值,这样子复杂度就变成了o(nm+n)
代码
# include<bits/stdc++.h>
using namespace std;
const int M = 1e4+10,N = 5e3+10;
struct edge
{
int x,y,w;
}edge[2*M+10];int cnt = 0; //无向图,存边数组要开成2*M
int dist1[N],dist2[N],dist3[N],dist[N]; //前三个数组分别以a,b,c为原点
int n,m;
int a,b,c;
void bellmanford(int x)
{
memset(dist,0x3f,sizeof dist);
dist[x] = 0;
while(true)
{
bool flag = false;
for(int i=1;i<=cnt;i++)
{
int u = edge[i].x,v = edge[i].y,d = edge[i].w;
if(dist[v]>dist[u]+d)
{
flag = true;
dist[v] = dist[u]+d;
}
}
if(!flag) break;
}
}
int main()
{
cin>>n>>m;
for(int i=0;i<m;i++)
{
int x,y,z;
cin>>x>>y>>z;
edge[++cnt].x = x,edge[cnt].y = y,edge[cnt].w = z; //无向图,起点和终点可以互换
edge[++cnt].x = y,edge[cnt].y = x,edge[cnt].w = z;
}
cin>>a>>b>>c;
bellmanford(a);memcpy(dist1,dist,sizeof dist); //每次将dist拷贝到各自dist数组
bellmanford(b);memcpy(dist2,dist,sizeof dist);
bellmanford(c);memcpy(dist3,dist,sizeof dist);
int ans = 2e9;
for(int i=1;i<=n;i++) ans = min(ans,dist1[i]+dist2[i]+dist3[i]);
cout<<ans<<endl;
return 0;
}
例题3
小蜗想要完成一次说走就走的旅行,他来到了某旅行社进行咨询。
地图可以看做是一张 n 个顶点 m 条边的无向简单图,顶点编号从 1 到 n,每个顶点表示一座城市,在两个城市之间移动需要花费连接这两座城市的边的边权的代价。
小蜗是这家旅行社的vip用户,他拥有 k 张打折券,在一次移动中他可以使用一张打折券,使得这次移动的代价变成之前的一半,每条边只能使用一张打折券。
小蜗现在在 1 号城市,他想知道他最少需要花费多少代价可以到达 n 号城市,数据保证 1 号城市和 n 号城市两地连通。
输入格式
第一行三个整数 n,m,k 表示图的顶点数(也就是城市数)、边数和打折券的数量。
接下来 m 行,每行三个整数 x,y,z,表示 x 号城市和 y 号城市之间有一条边权为 z 的边。
输出格式
输出一行一个数表示答案。
样例输入
3 2 1
1 2 4
2 3 6
样例输出7
数据规模对于所有数据,保证 2≤n≤500,1≤m≤2000,1≤k≤10,1≤x,y≤n,1≤z≤10000 保证 z 是偶数。文章来源:https://www.toymoban.com/news/detail-582264.html
我们可以设一个二维状态数组 f[i][j] 为 到第i个点用了j个打折券花费的最少代价
bellman-ford最本质的思想其实是一个点到另一个点的最短路径可以通过每个边松弛最多n次得到。那么我们应该也可以通过这种方法实现从一个状态到另一个状态。遍历每条边,起点x 终点y 权值w,那么状态一共有2*k-1种变化可能 即对于每个状态有不用代价卷和用代价卷两种可能,当代价卷用完了那只有不用代价卷这一种可能
最后的结果就是f[n][i] (i == 0,1,2...k) 的最小值文章来源地址https://www.toymoban.com/news/detail-582264.html
代码
# include<bits/stdc++.h>
using namespace std;
const int M = 2e3 , N = 510;
struct edge
{
int x,y,w;
}edge[2*M+10];
int cnt = 0;
int f[N][11];
int n,m,k;
void bellmanford(int a,int b)
{
memset(f,0x3f,sizeof f);
f[a][0] = 0;
for(int i=1;i<=n;i++)
{
for(int j=0;j<cnt;j++)
{
int x = edge[j].x,y = edge[j].y,w = edge[j].w;
for(int l=0;l<=k;l++)
{
if(f[y][l]>f[x][l]+w)
{
f[y][l] = f[x][l]+w; //不花费打折券
}
if(l<k && f[y][l+1]>f[x][l]+w/2)
//花费打折券,当i==k即没有打折卷可用的时候不执行
{
f[y][l+1] = f[x][l]+w/2;
}
}
}
}
}
int main()
{
scanf("%d%d%d",&n,&m,&k);
for(int i=0;i<m;i++)
{
int x,y,w;cin>>x>>y>>w;
edge[++cnt].x = x;edge[cnt].y = y;edge[cnt].w = w;
edge[++cnt].x = y;edge[cnt].y = x;edge[cnt].w = w;
}
bellmanford(1,n);
int ans = 0x3f3f3f3f;
for(int i=0;i<=k;i++) ans = min(ans,f[n][i]); //最小值即为答案
cout<<ans<<endl;
return 0;
}
到了这里,关于最短路之 Bellman-ford 算法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!