回归决策树的介绍-Toy模板网

这篇具有很好参考价值的文章主要介绍了回归决策树的介绍。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

回归决策树（Regression Decision Tree）是一种决策树算法，用于解决回归问题。与传统的分类决策树不同，回归决策树的目标是预测连续数值型的输出，而不是离散的类别标签。

数据集准备：

首先，需要准备训练数据集，包括输入特征和对应的输出值。每个样本都有一组特征值和一个连续数值型的输出。
特征选择：

选择最佳的特征来划分数据集。常用的划分准则包括平方误差（Mean Squared Error, MSE）和平均绝对误差（Mean Absolute Error, MAE）等。目标是选择划分后的子集使得预测值与实际值之间的误差最小化。
构建决策树：

通过递归地选择最佳的特征和划分点，不断地划分数据集，直到满足终止条件。终止条件可以是达到最大深度、节点中的样本数量达到阈值等。
叶节点的预测值：

当停止划分时，每个叶节点上都有一个预测值，表示在该区域中的样本的输出值的预测。可以选择样本在该区域中的平均值作为叶节点的预测值。
预测：

使用构建好的回归决策树来进行预测。给定一个新的输入特征向量，通过沿着树的路径进行判断，最终到达叶节点并得到预测值。

回归决策树和分类决策树是两种不同的决策树算法，它们在目标变量类型、划分准则和输出值处理等方面存在一些区别。

目标变量类型：
- 回归决策树：回归决策树用于解决回归问题，其中目标变量是连续数值型的。它预测的是输入特征对应的数值输出。
- 分类决策树：分类决策树用于解决分类问题，其中目标变量是离散的类别标签。它预测的是输入特征对应的类别。
划分准则：
- 回归决策树：回归决策树在划分过程中使用回归相关的准则，如平方误差（Mean Squared Error, MSE）或平均绝对误差（Mean Absolute Error, MAE），以最小化预测值与实际值之间的误差。
- 分类决策树：分类决策树在划分过程中使用分类相关的准则，如基尼指数（Gini index）或信息增益（Information Gain），以最大化类别的纯度或最小化不确定性。
输出值处理：
- 回归决策树：回归决策树在每个叶节点上有一个预测值，表示该区域中样本的输出预测。可以选择样本在该区域中的平均值作为叶节点的预测值。
- 分类决策树：分类决策树在每个叶节点上有一个主要的类别标签，表示该区域中样本的预测类别。可以选择区域中出现最频繁的类别作为叶节点的预测类别。

需要根据具体的问题和目标变量类型选择适合的决策树算法。如果目标变量是连续的数值型，可以使用回归决策树；如果目标变量是离散的类别标签，可以使用分类决策树。

回归决策树和线性回归是两种不同的回归方法，它们在建模方式、拟合能力和解释性等方面存在一些区别。

建模方式：
- 回归决策树：回归决策树使用树结构来建立输入特征与输出之间的映射关系。它通过递归地选择最佳的特征和划分点来划分数据集，每个叶节点上都有一个预测值表示该区域中样本的输出预测。
- 线性回归：线性回归是一种基于线性模型的回归方法。它假设输出与输入之间存在线性关系，通过拟合最佳的线性函数来进行预测。
拟合能力：
- 回归决策树：回归决策树可以适应非线性的关系，能够处理复杂的数据分布和非线性特征交互。它可以根据数据的分布自动选择不同的划分特征和划分点，具有一定的拟合灵活性。
- 线性回归：线性回归适用于线性关系的建模，它通过拟合一个线性函数来进行预测。当数据存在复杂的非线性关系时，线性回归的拟合能力相对较弱。
解释性：
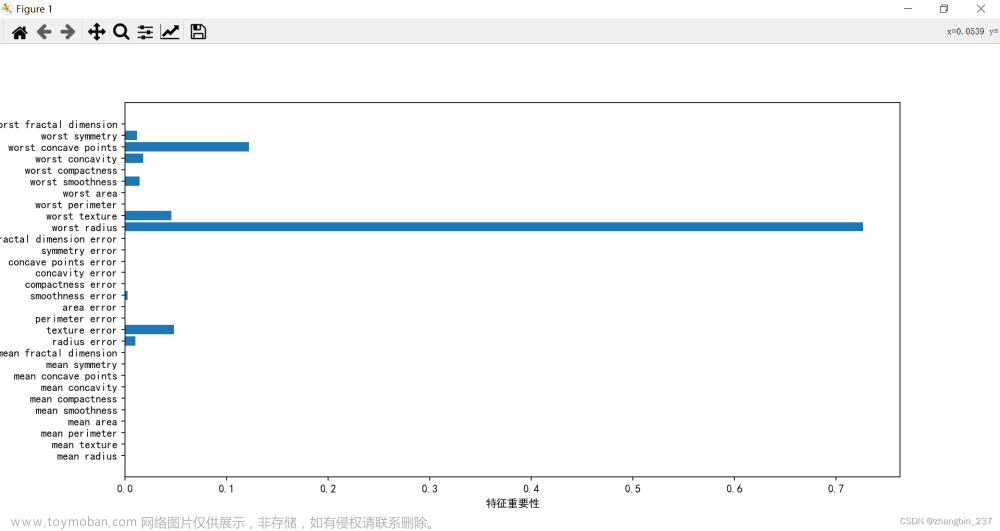
- 回归决策树：回归决策树具有很好的解释性，可以直观地表示特征的重要性和决策过程。它可以生成一棵可解释的树结构，帮助理解数据的特征重要性和特征之间的关系。
- 线性回归：线性回归的解释性相对较强，可以通过系数来解释各个特征对输出的贡献程度。系数的正负表示特征的影响方向，绝对值大小表示影响的程度。