使用ARIMA进行时间序列预测|就代码而言-Toy模板网

这篇具有很好参考价值的文章主要介绍了使用ARIMA进行时间序列预测|就代码而言。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

import pandas as pd
from statsmodels.tsa.arima.model import ARIMA

# 示例使用
data = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

# 将数据转换为时间序列对象
time_series = pd.Series(data)

# 拟合ARIMA模型
model = ARIMA(time_series, order=(1, 0, 0))
model_fit = model.fit()

# 进行预测
forecast = model_fit.predict(start=len(time_series), end=len(time_series)+4)
print(forecast)

model.fit().predict()函数参数的意思

model.fit()函数是用来拟合ARIMA模型的，它会根据提供的时间序列数据来估计模型的参数。在这个函数中，没有需要指定额外的参数。

model.predict()函数是用来进行时间序列的预测的，它可以在拟合后的模型上进行预测。在进行预测时，需要指定预测的起始时间步和结束时间步。在predict()函数中，可以使用两种方式来指定预测的时间步：

指定预测的起始时间步和结束时间步的索引位置。例如，start=len(time_series)表示从时间序列的最后一个时间步开始预测，end=len(time_series)+4表示预测到时间序列的最后一个时间步后的第4个时间步。

指定预测的起始时间步和预测的步数。例如，start=len(time_series)表示从时间序列的最后一个时间步开始预测，steps=5表示预测5个时间步。

根据具体的需求，可以选择其中一种方式来指定预测的时间步。在示例代码中，我们使用了第一种方式，即指定了预测的起始时间步和结束时间步的索引位置。

希望这样解释清楚了model.fit().predict()函数参数的意思。如果还有任何疑问，请随时提问。

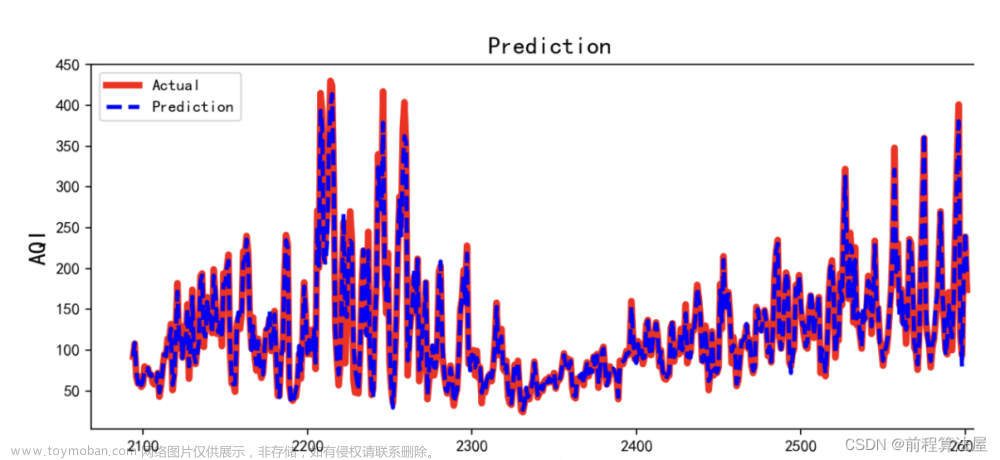
要衡量ARIMA模型的预测精度，可以使用均方根误差（RMSE）或平均绝对误差（MAE）等指标。以下是使用均方根误差的示例代码：

import pandas as pd
from statsmodels.tsa.arima.model import ARIMA
from sklearn.metrics import mean_squared_error

# 示例使用
# data = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
# 
data = [1.310, 1.307, 1.307, 1.307]

# 将数据转换为时间序列对象
time_series = pd.Series(data)

# 拟合ARIMA模型
model = ARIMA(time_series, order=(1, 0, 0))
model_fit = model.fit()

# 进行预测
forecast = model_fit.predict(start=len(time_series), end=len(time_series)+1)

# 计算均方根误差
actual_values = [1.307, 1.307]  # 实际值
mse = mean_squared_error(actual_values, forecast)
rmse = np.sqrt(mse)
print("均方根误差 (RMSE):", rmse)

Reference

OpenAI-ChatGPT文章来源地址https://www.toymoban.com/news/detail-585889.html

到了这里，关于使用ARIMA进行时间序列预测|就代码而言的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！